- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Теория графов (10 класс)
Содержание
- 1. Презентация по математике на тему Теория графов (10 класс)
- 2. Основные понятия теории графов. Теория графов -
- 3. Дискретная математика. Топология Тополо́гия — раздел математики, изучающий в
- 4. Терминология.Граф - совокупность конечного числа точек, называемых вершинами графа, и
- 5. Обозначение: Kn – граф, состоящий из n вершин и ребер, соединяющих
- 6. История возникновения теорииРодоначальником теории графов считается Леонард Эйлер.
- 7. Леонард Эйлер (1707-1783)Л. Эйлер — ученый необычайной
- 8. Дом, где жил Л. Эйлер в 1766-1783
- 9. Леонард Эйлер
- 10. Память Мемориальная доска на доме Эйлера в Берлине Серебряная монета России 2007 годаШвейцарская банкнота
- 11. Возникновение теории. Проблема семи мостов Кёнигсберга. Из
- 12. Проблема семи мостов Кёнигсберга*Граф называется эйлеровым, если
- 13. Выведенные свойства Число нечётных вершин (вершин, к
- 14. Классические задачи
- 15. Проблема четырех красокПроблема четырёх красок — математическая
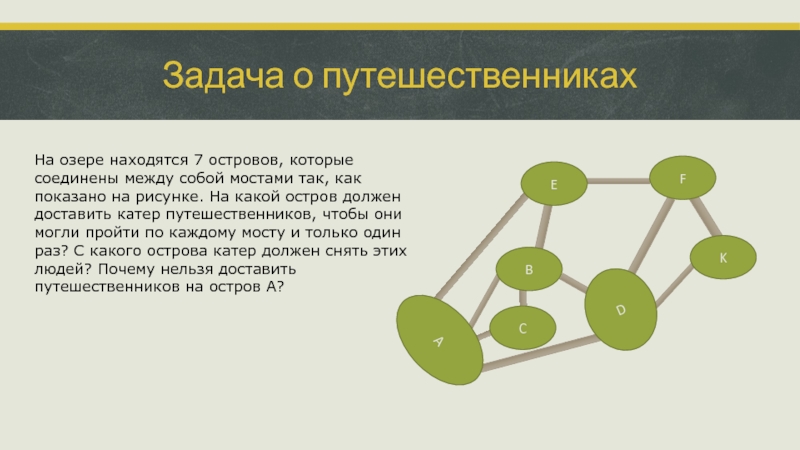
- 16. Задача о путешественниках На озере находятся 7
- 17. Использование теории графовТеория графов – одна из
- 18. В химииХимическая графы дают возможность прогнозировать химический превращения,
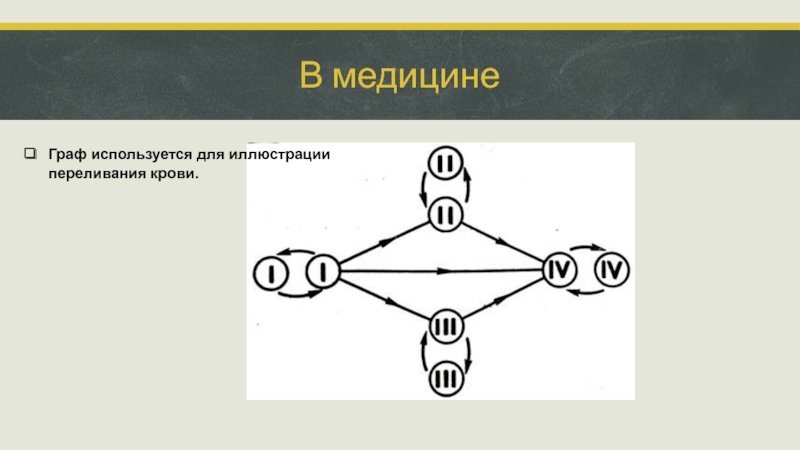
- 19. В медицине Граф используется для иллюстрации переливания крови.
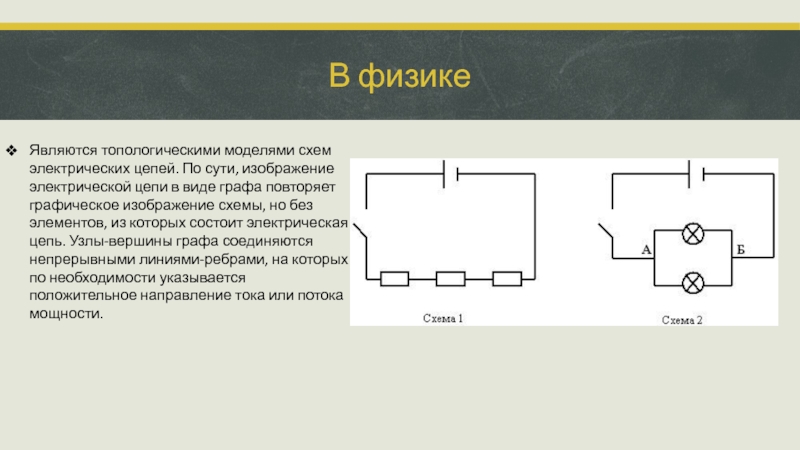
- 20. В физике Являются топологическими моделями схем электрических
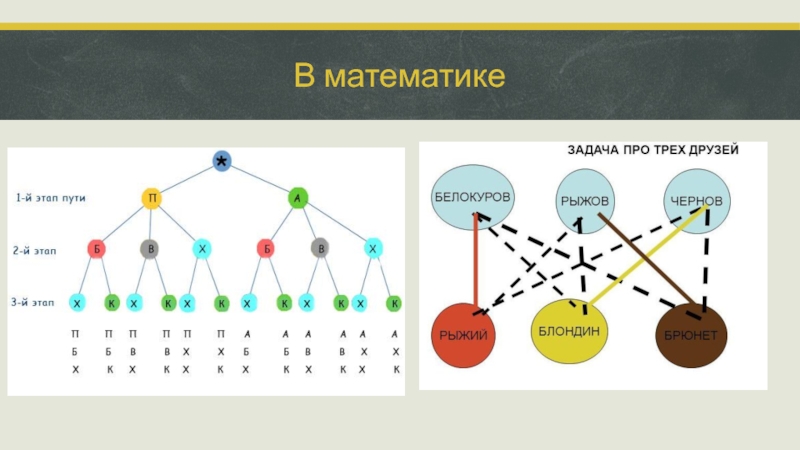
- 21. В математикеВ математике графы применяются для решения
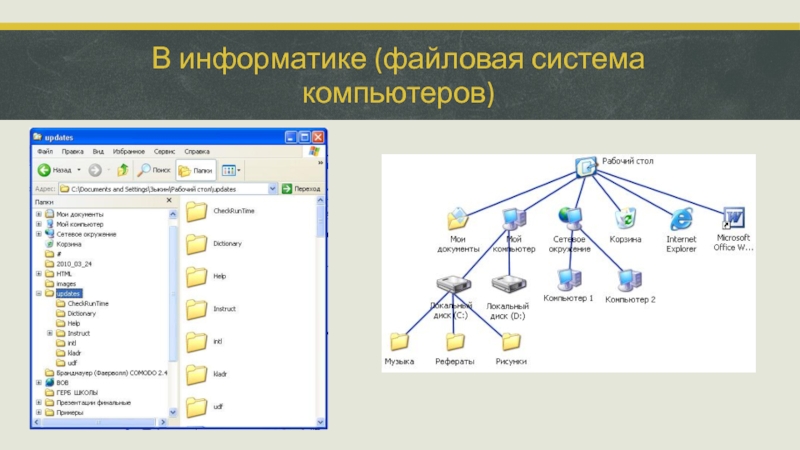
- 22. В информатике (файловая система компьютеров)
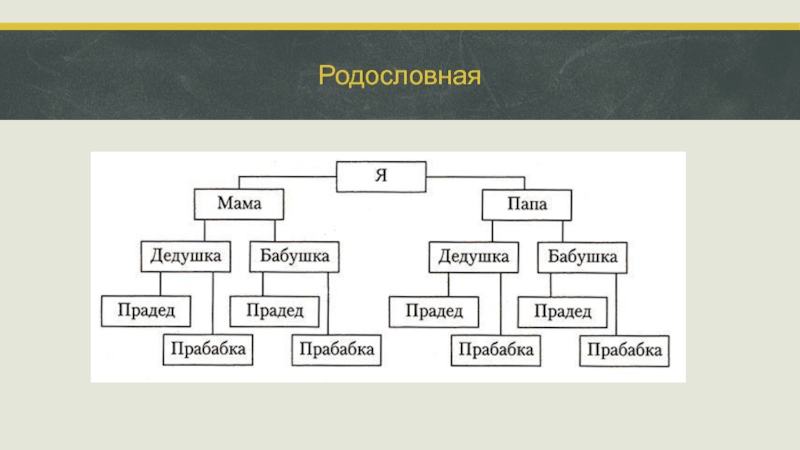
- 23. Родословная
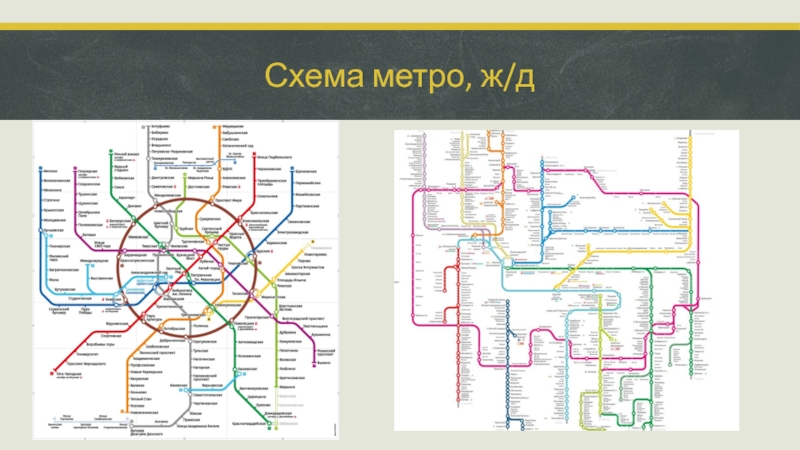
- 24. Схема метро, ж/д
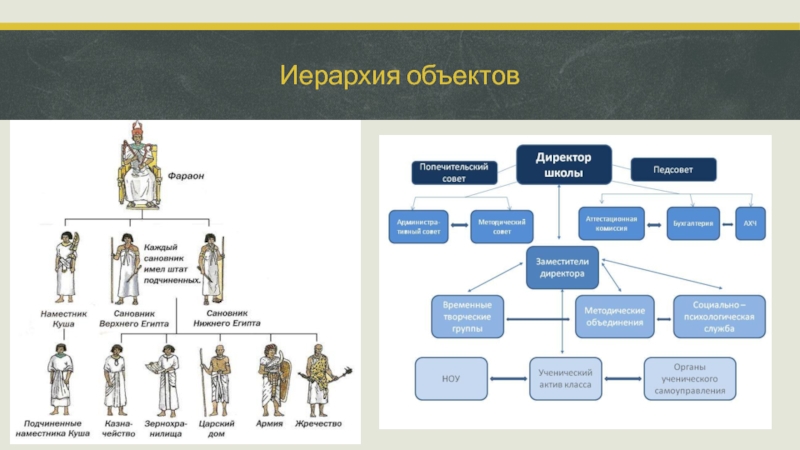
- 25. Иерархия объектов
- 26. Обобщение БиологииТеории массового обслуживанияМатематике (экономике, комбинаторике)СтроительствеЭлектротехникеМенеджментеЛогистикеГеографииМашиностроенииСоциологииПрограммированииАвтоматизации технологических процессовХимииФизике Медицине Графы широко используются в
- 27. Спасибо за внимание!
Слайд 2Основные понятия теории графов.
Теория графов - в узком смысле -
Слайд 3Дискретная математика. Топология
Тополо́гия — раздел математики, изучающий в самом общем виде явление непрерывности,
Дискре́тная матема́тика — часть математики, изучающая дискретные математические структуры
Дискре́тность— свойство, противопоставляемое непрерывности, прерывность. Под дискретностью понимают:
Нечто, изменяющееся между несколькими различными стабильными состояниями.
Нечто, состоящее из отдельных частей, прерывистость, дробность.
Слайд 4Терминология.
Граф - совокупность конечного числа точек, называемых вершинами графа, и попарно соединяющих некоторые из
Дерево — это связный граф без циклов, имеющий исходную вершину (корень) и крайние вершины; пути от исходной вершины к крайним вершинам называются ветвями
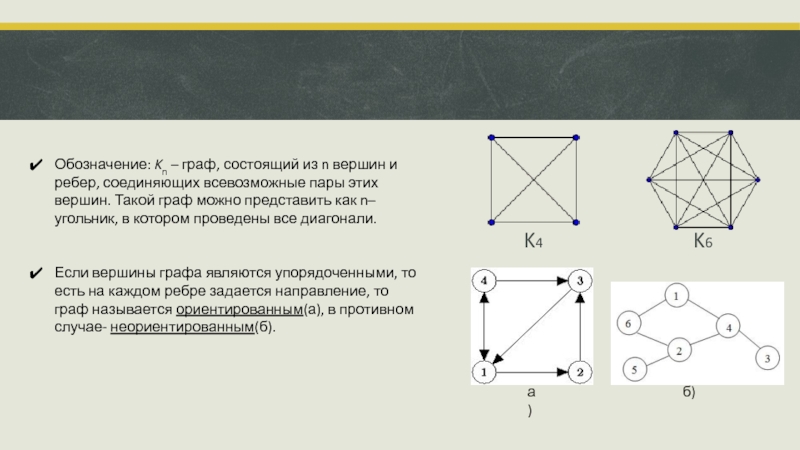
Слайд 5Обозначение: Kn – граф, состоящий из n вершин и ребер, соединяющих всевозможные пары этих вершин.
K4
K6
Если вершины графа являются упорядоченными, то есть на каждом ребре задается направление, то граф называется ориентированным(а), в противном случае- неориентированным(б).
а)
б)
Слайд 6История возникновения теории
Родоначальником теории графов считается Леонард Эйлер. В 1736 году в
Слайд 7Леонард Эйлер (1707-1783)
Л. Эйлер — ученый необычайной широты интересов и творческой
Слайд 8Дом, где жил Л. Эйлер в 1766-1783 гг. (реконструкция)
Титульный лист 'Опыта
Слайд 10Память
Мемориальная доска на доме Эйлера в Берлине
Серебряная монета России
Швейцарская банкнота
Слайд 11Возникновение теории. Проблема семи мостов Кёнигсберга.
Из письма Эйлера к итальянскому
"Некогда мне была предложена задача об острове, расположенном в городе Кенигсберге и окруженном рекой, через которую перекинуто семь мостов. Спрашивается, может ли кто-нибудь непрерывно обойти их, проходя только однажды через каждый мост. И тут же мне было сообщено, что никто еще до сих пор не мог это проделать, но никто и не доказал, что это невозможно. Вопрос этот, хотя и банальный, показался мне, однако, достойным внимания тем, что для его решения недостаточны ни геометрия, ни алгебра, ни комбинаторное искусство. После долгих размышлений я нашел легкое правило, основанное на вполне убедительном доказательстве, с помощью которого можно во всех задачах такого рода тотчас же определить, может ли быть совершен такой обход через какое угодно число и как угодно расположенных мостов или не может. Кенигсбергские же мосты расположены так, что их можно представить на следующем рисунке, на котором A обозначает остров, а B, C и D – части континента, отделенные друг от друга рукавами реки. Семь мостов обозначены буквами a, b, c, d, e, f, g ".
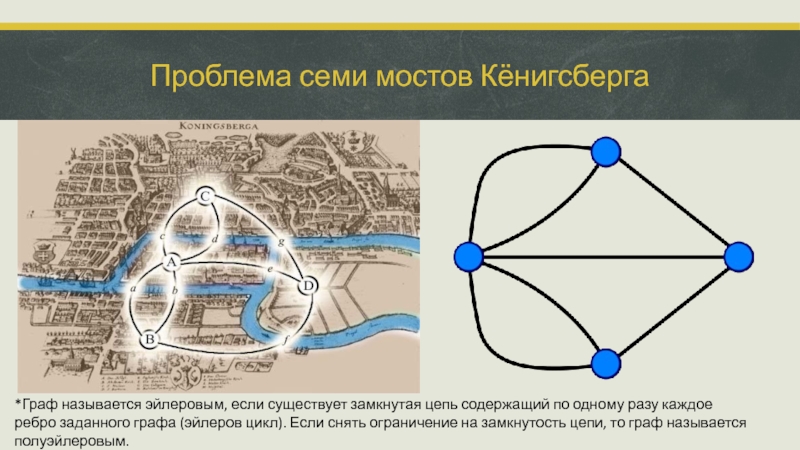
Слайд 12Проблема семи мостов Кёнигсберга
*Граф называется эйлеровым, если существует замкнутая цепь содержащий
Слайд 13Выведенные свойства
Число нечётных вершин (вершин, к которым ведёт нечётное число
Если все вершины графа чётные, то можно, не отрывая карандаша от бумаги, начертить граф, при этом можно начинать с любой вершины графа и завершить его в той же вершине.
Граф с более чем двумя нечётными вершинами невозможно начертить одним росчерком. Граф кёнигсбергских мостов имел четыре (синим) нечётные вершины (то есть все), следовательно, невозможно пройти по всем мостам, не проходя ни по одному из них дважды.
Число нечетных вершин графа всегда четно.
Если в графе имеются нечетные вершины, то наименьшее число росчерков, которыми можно нарисовать граф, равно половине числа нечетных вершин этого графа. Граф, имеющий две и только две нечетных вершины, можно начертить одним росчерком, если начать движение с одной нечетной вершины и закончить его в другой.
Слайд 15Проблема четырех красок
Проблема четырёх красок — математическая задача, предложенная Гутри в
Выяснить, можно ли всякую расположенную на сфере карту раскрасить четырьмя красками так, чтобы любые две области, имеющие общий участок границы, были раскрашены в разные цвета.
Иначе говоря, показать что хроматическое число плоского графа не превосходит 4.
*Хроматическое число графа G — минимальное число цветов, в которые можно раскрасить вершины графа G так, чтобы концы любого ребра имели разные цвета.
Слайд 16Задача о путешественниках
На озере находятся 7 островов, которые соединены между
A
C
B
D
K
F
E