- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Теорема Пифагора(8 класс)
Содержание
- 1. Презентация по математике на тему Теорема Пифагора(8 класс)
- 2. 1.Найдите площадь квадрата со стороной3 см; 1,2
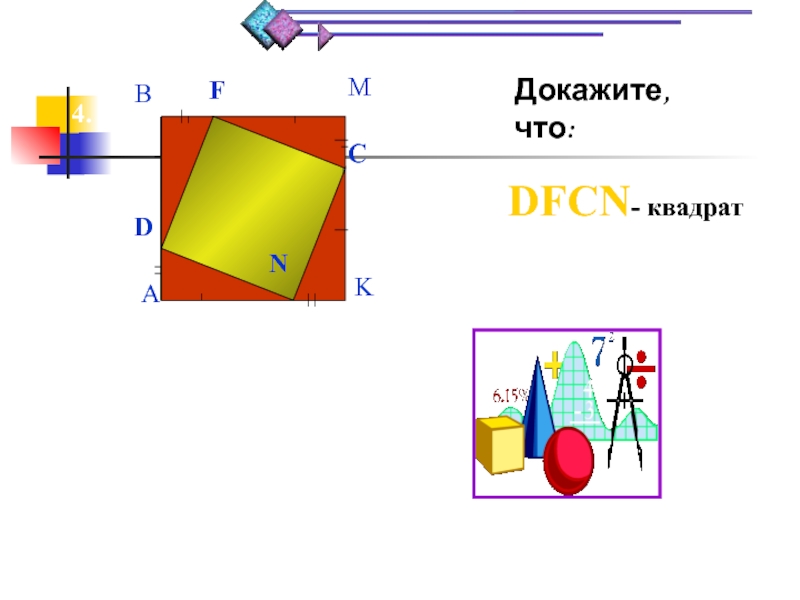
- 3. Докажите,что:DFCN- квадрат4.DFCNABMK
- 4. «Геометрия обладает двумя великими сокровищами.Первое – это
- 5. Знаменитый древнегреческий философ и математик Пифагор Самосский
- 6. Здесь в Кретоне, рождается школа Пифагора. В
- 7. Слайд 7
- 8. abcabcabcabcВ прямоугольном треугольникеквадрат гипотенузы равенсумме квадратов катетов .а2+в2=с2Доказательство:S =(а+в)2S=c2+4·1/2ab(а+в)2=с2+4·1/2ава2+2ав+в2=с2+2ава2+в2=с2Теорема Пифагора
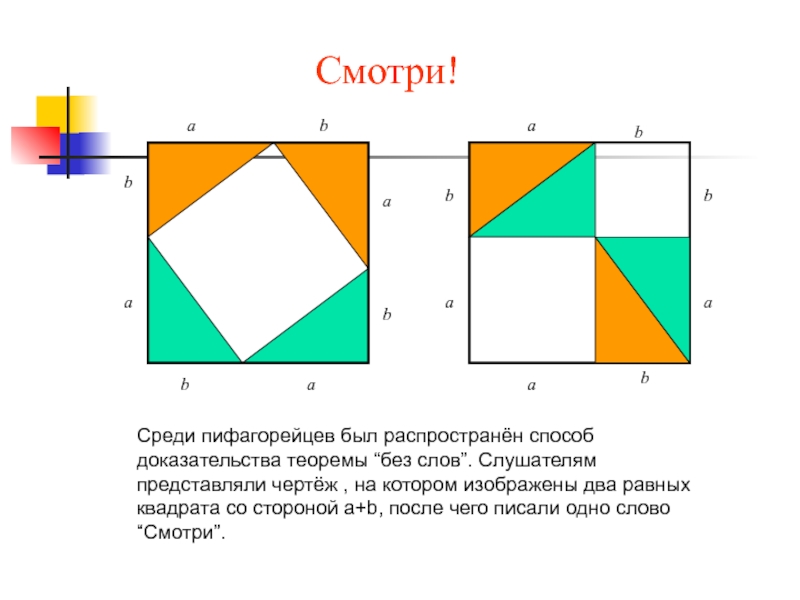
- 9. aaaaaaaabbbbbbbbСмотри!Среди пифагорейцев был распространён способ доказательства теоремы
- 10. К теореме Пифагора его ученики составляли
- 11. Слайд 11
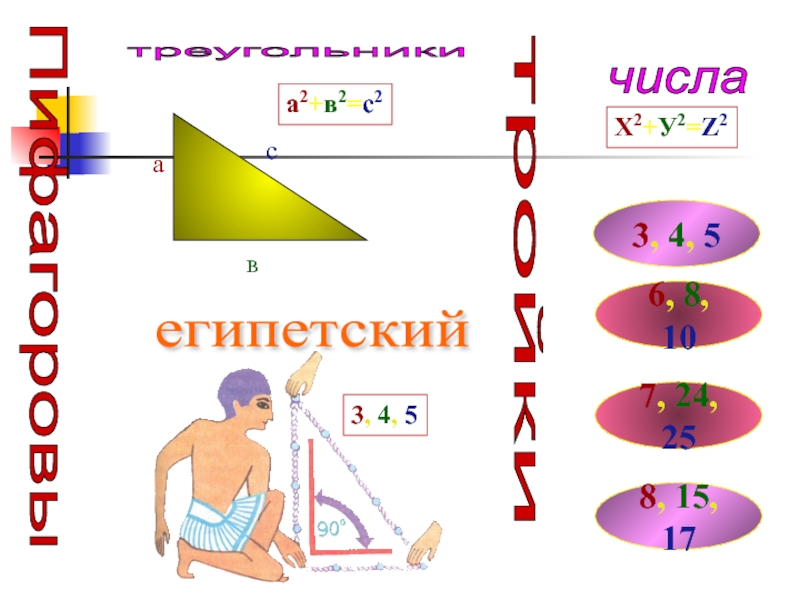
- 12. Пифагоровы тройки числа треугольники Х2+У2=Z23, 4, 56, 8, 107, 24, 258, 15, 17асва2+в2=с2египетский 3, 4, 5
- 13. С глубокой древности математики находят все новые
- 14. Слайд 14
- 15. Если дан нам треугольникИ притом с прямым
1.Найдите площадь квадрата со стороной3 см; 1,2 мм; 5\7 м; см; а см .2. Найдите площадь прямоугольноготреугольника с катетами 3 см и 4 см;2,2 м и 5 см; а см и
Слайд 2
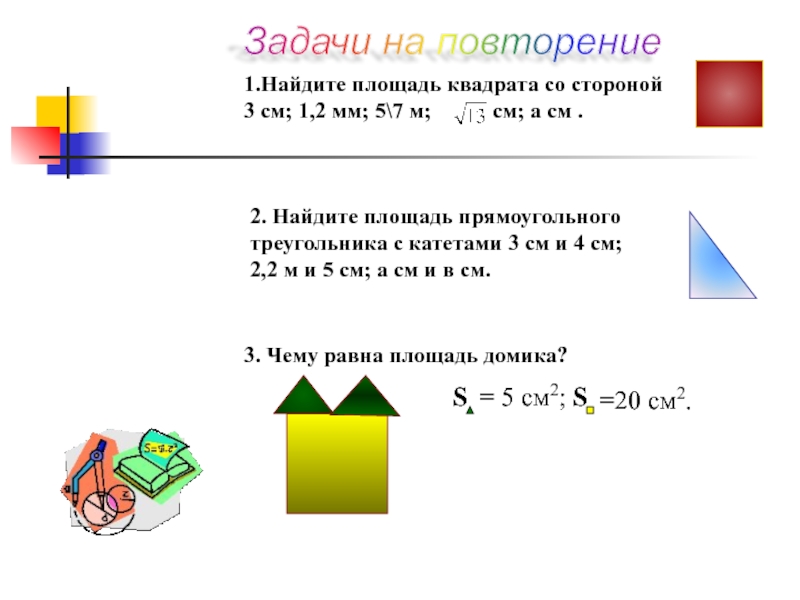
1.Найдите площадь квадрата со стороной
3 см; 1,2 мм; 5\7 м;
см; а см .
2. Найдите площадь прямоугольного
треугольника с катетами 3 см и 4 см;
2,2 м и 5 см; а см и в см.
3. Чему равна площадь домика?
S
= 5 см2; S
=20 см2.
Задачи на повторение
Слайд 4«Геометрия обладает двумя великими сокровищами.Первое – это теорема Пифагора…»
О Пифагоре сохранились
десятки легенд и мифов, с его именем связано многое в математике, и в первую очередь, конечно, теорема носящая его имя, которая занимает важнейшее место в школьном курсе геометрии.
ИСТОРИЧЕСКАЯ СПРАВКА
Слайд 5Знаменитый древнегреческий философ и математик Пифагор Самосский родился на острове Самос,
далеко от Греции в 580
году до н. э. По античным свидетельствам он был красив и обладал незаурядными способностями. Совсем юношей он покинул родину, прошел по дорогам Египта и 12 лет жил в Вавилоне. После возвращения домой Пифагор переселился в Италию, затем в Сицилию.
году до н. э. По античным свидетельствам он был красив и обладал незаурядными способностями. Совсем юношей он покинул родину, прошел по дорогам Египта и 12 лет жил в Вавилоне. После возвращения домой Пифагор переселился в Италию, затем в Сицилию.
580-500 г. до н. э.
Из жизни Пифагора
Слайд 6
Здесь в Кретоне, рождается школа Пифагора. В пифагорейской школе занимались изучением
чисел и их свойств,
много внимания уделяли музыке, живописи, физическому развитию, здоровью. Пифагор и его ученики были трудолюбивы и аскетичны.
много внимания уделяли музыке, живописи, физическому развитию, здоровью. Пифагор и его ученики были трудолюбивы и аскетичны.
Из жизни Пифагора
Слайд 8
a
b
c
a
b
c
a
b
c
a
b
c
В прямоугольном треугольнике
квадрат гипотенузы равен
сумме квадратов катетов .
а2+в2=с2
Доказательство:
S
=(а+в)2
S
=c2+4·1/2ab
(а+в)2=с2+4·1/2ав
а2+2ав+в2=с2+2ав
а2+в2=с2
Теорема Пифагора
Слайд 9
a
a
a
a
a
a
a
a
b
b
b
b
b
b
b
b
Смотри!
Среди пифагорейцев был распространён способ доказательства теоремы “без слов”. Слушателям представляли
чертёж , на котором изображены два равных квадрата со стороной a+b, после чего писали одно слово “Смотри”.
Слайд 10 К теореме Пифагора его ученики составляли стишки, вроде:
«Пифагоровы штаны
во все
стороны равны»,
А также рисовали такие карикатуры:
Шарж из учебника XVI века.
Слайд 12Пифагоровы
тройки
числа
треугольники
Х2+У2=Z2
3, 4, 5
6, 8, 10
7, 24, 25
8,
15, 17
а
с
в
а2+в2=с2
египетский
3, 4, 5
Слайд 13С глубокой древности математики находят все новые и новые доказательства теоремы
Пифагора, все новые и новые замыслы ее доказательств. Таких доказательств – более или менее строгих, более или менее наглядных – известно более полутора сотен (по другим источникам, более пятисот), но стремление к преумножению их числа сохранилось. Поэтому теорема Пифагора занесена в «Книгу рекордов Гиннеса».
Слайд 15
Если дан нам треугольник
И притом с прямым углом,
То квадрат гипотенузы
Мы всегда
легко найдем
Катеты в квадрат возводим,
Сумму степеней находим-
И таким простым путём
К результату мы придём
Заполните таблицу:
ЗАДАЧА
