- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Свойства функции (9 класс)
Содержание
- 1. Презентация по математике на тему Свойства функции (9 класс)
- 2. Устная работа F(x) = Х2 - 8хнайдитеF(0), F(-1), F(3),
- 3. Найдите область определения функции
- 4. Найдите область определения функции
- 5. Найдите область определения функции
- 6. Числовой функцией называется соответствие (зависимость), при котором
- 7. Способы задания функций- Аналитический (с помощью формулы) - Графический- Табличный- Описательный (словесное описание)Сила равна скорости изменения импульса
- 8. График функции Графиком функции f называют
- 9. 1. Область определения2. Область значений3. Нули функции4.
- 10. Нулем функции y = f (x) называется
- 11. 4. ЧетностьЧетная функцияНечетная функцияФункция y = f(x)
- 12. 5. Промежутки знакопостоянстваПромежутки, на которых непрерывная функция
- 13. 6. Непрерывность Функция называется непрерывной на промежутке,
- 14. 7. Монотонность Функцию у = f(х) называют
- 15. Слайд 15
- 16. 9. ОграниченностьФункцию у = f(х) называют ограниченной
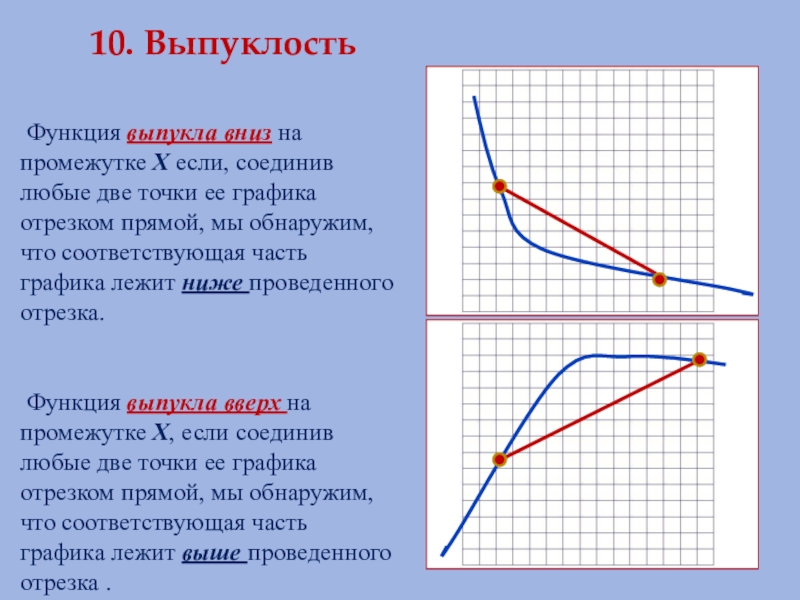
- 17. 10. Выпуклость Функция выпукла вниз на промежутке
- 18. Самостоятельная работа
- 19. Слайд 19
- 20. Выполни задание
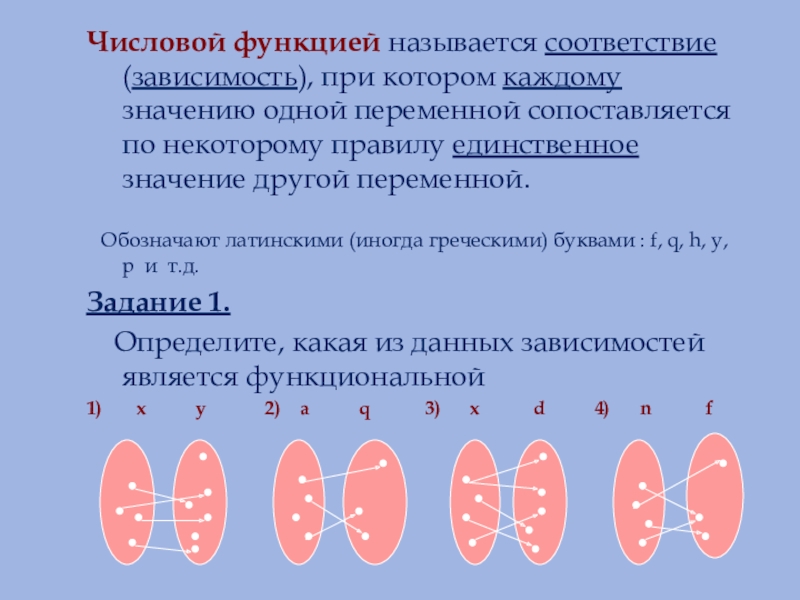
Слайд 6Числовой функцией называется соответствие (зависимость), при котором каждому значению одной переменной
Обозначают латинскими (иногда греческими) буквами : f, q, h, y, p и т.д.
Задание 1.
Определите, какая из данных зависимостей является функциональной
1) x y 2) a q 3) x d 4) n f
Слайд 7Способы задания функций
- Аналитический (с помощью формулы)
- Графический
- Табличный
- Описательный (словесное
Сила равна скорости изменения импульса
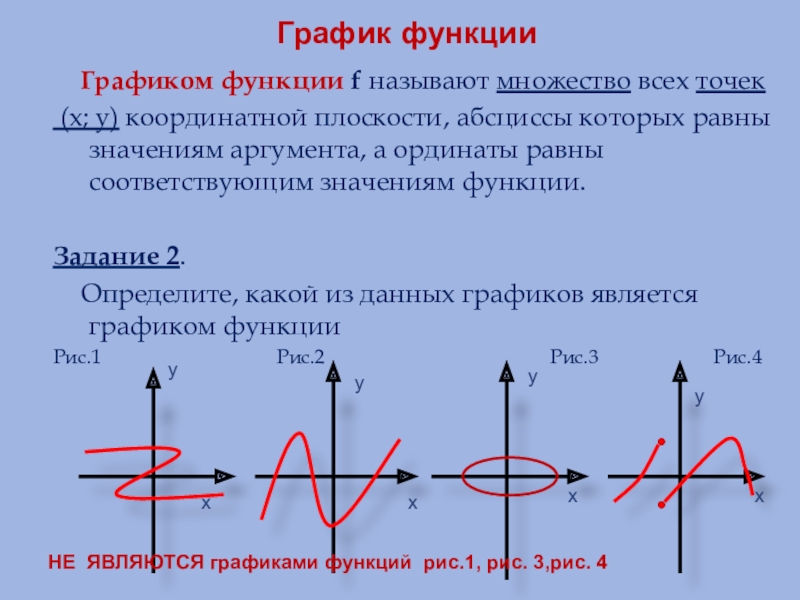
Слайд 8График функции
Графиком функции f называют множество всех точек
Задание 2.
Определите, какой из данных графиков является графиком функции
Рис.1 Рис.2 Рис.3 Рис.4
у
у
у
у
х
х
х
х
НЕ ЯВЛЯЮТСЯ графиками функций рис.1, рис. 3,рис. 4
Слайд 91. Область определения
2. Область значений
3. Нули функции
4. Четность
5. Промежутки знакопостоянства
6. Непрерывность
7.
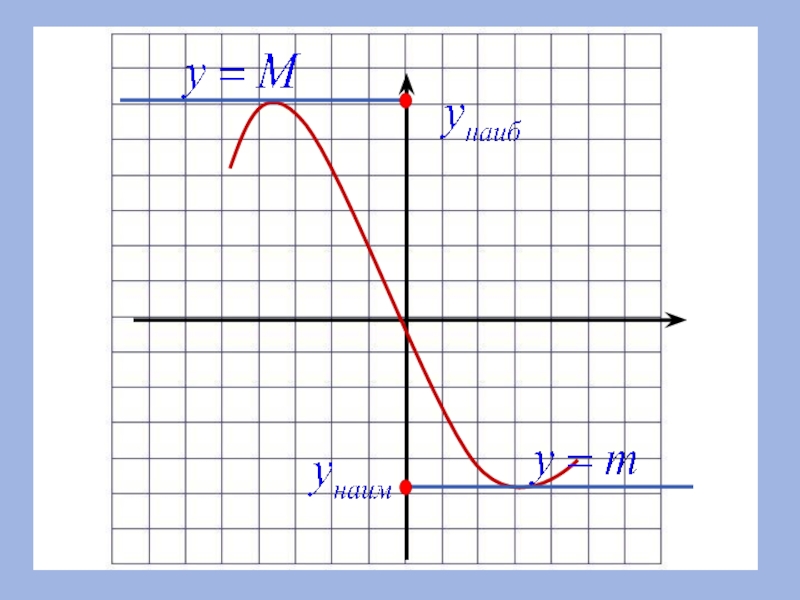
8. Наибольшее и наименьшее значения
9. Ограниченность
10. Выпуклость
Свойства функции
Алгоритм описания свойств функции
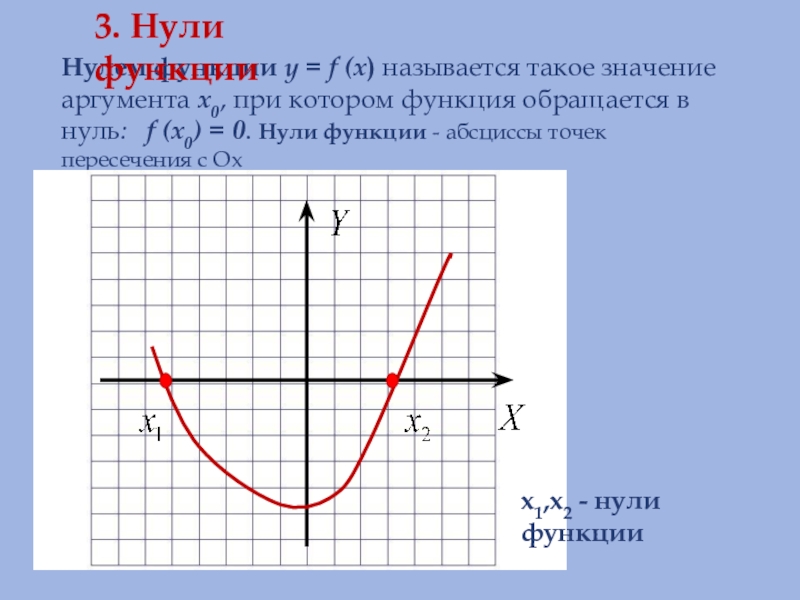
Слайд 10Нулем функции y = f (x) называется такое значение аргумента x0,
3. Нули функции
x1,x2 - нули функции
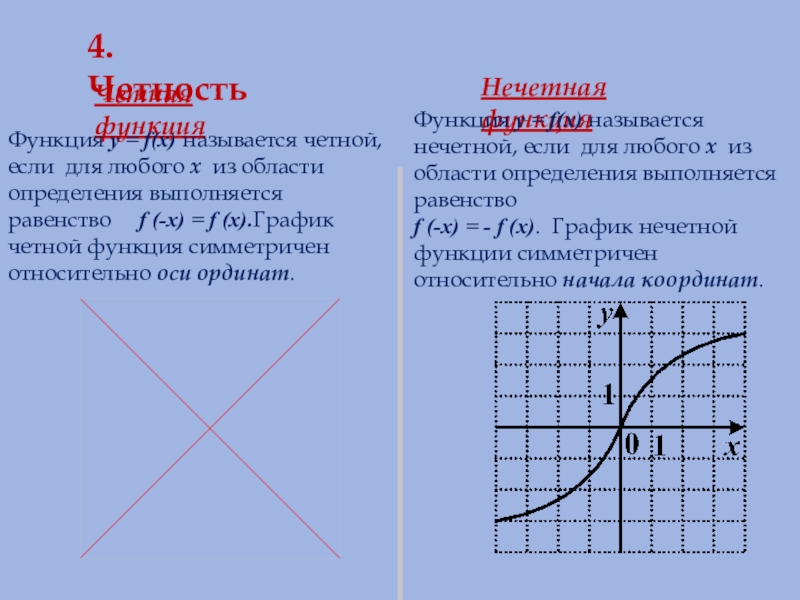
Слайд 114. Четность
Четная функция
Нечетная функция
Функция y = f(x) называется четной, если для
Функция y = f(x) называется нечетной, если для любого х из области определения выполняется равенство
f (-x) = - f (x). График нечетной функции симметричен относительно начала координат.
Слайд 125. Промежутки знакопостоянства
Промежутки, на которых непрерывная функция сохраняет свой знак и
y > 0 (график расположен выше оси ОХ) при х (- ∞; 1) U
(3; +∞),
y<0 (график расположен ниже OX) при х (1;3)
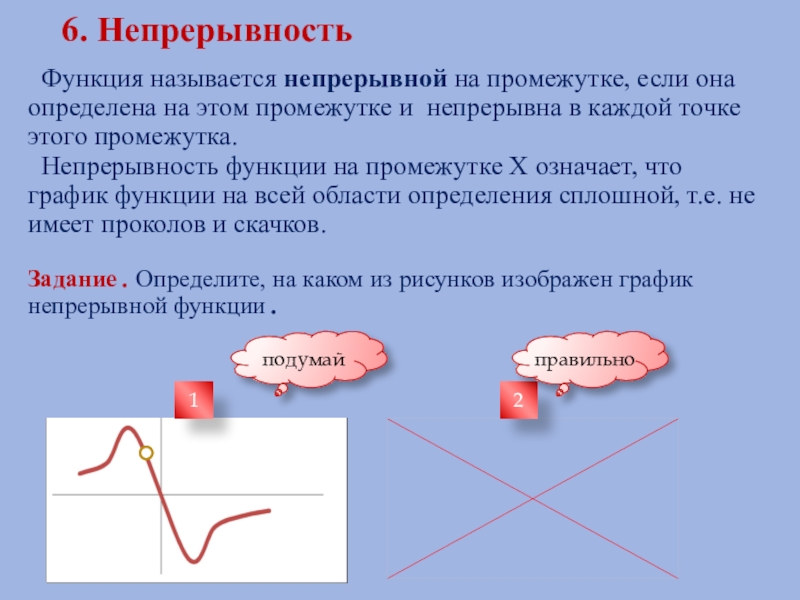
Слайд 136. Непрерывность
Функция называется непрерывной на промежутке, если она определена на
Непрерывность функции на промежутке Х означает, что график функции на всей области определения сплошной, т.е. не имеет проколов и скачков.
Задание . Определите, на каком из рисунков изображен график непрерывной функции .
1
2
подумай
правильно
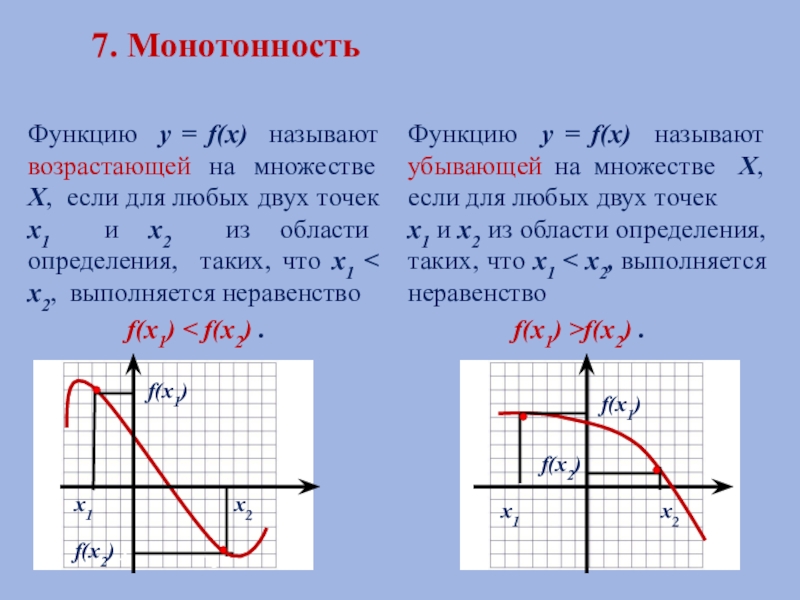
Слайд 147. Монотонность
Функцию у = f(х) называют возрастающей
f(х1) < f(х2) .
Функцию у = f(х) называют убывающей на множестве Х, если для любых двух точек
х1 и х2 из области определения, таких, что х1 < х2, выполняется неравенство
f(х1) >f(х2) .
x1
х1
x2
f(x2)
f(x1)
x2
x1
x2
f(x2)
f(x1)
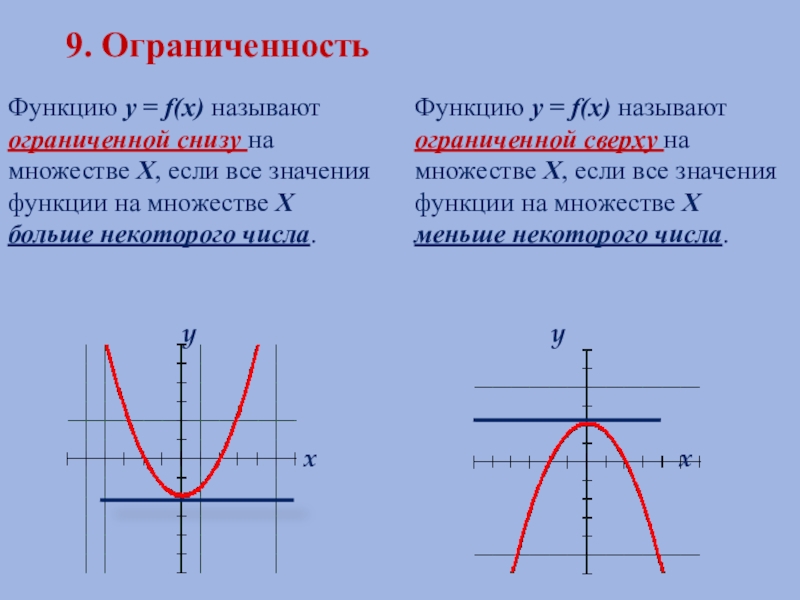
Слайд 169. Ограниченность
Функцию у = f(х) называют ограниченной снизу на множестве Х,
Функцию у = f(х) называют ограниченной сверху на множестве Х, если все значения функции на множестве Х меньше некоторого числа.
х
у
х
у
Слайд 1710. Выпуклость
Функция выпукла вниз на промежутке Х если, соединив любые
Функция выпукла вверх на промежутке Х, если соединив любые две точки ее графика отрезком прямой, мы обнаружим, что соответствующая часть графика лежит выше проведенного отрезка .