- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему: Решение задач на проценты с помощью MS Excel (9 класс)
Содержание
- 1. Презентация по математике на тему: Решение задач на проценты с помощью MS Excel (9 класс)
- 2. Простой процентный рост
- 3. Под наращенной суммой ссуды (долга,
- 4. Первый член этой прогрессии равен S0, разность
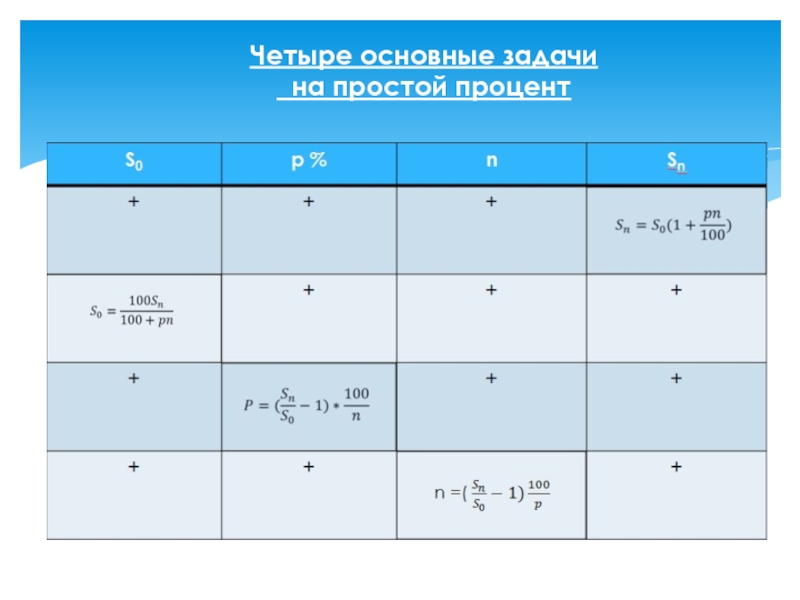
- 5. Четыре основные задачи на простой процент
- 6. Задача №1Вкладчик открыл в банке счёт и
- 7. Задача №2Какую сумму положили в банк под
- 8. Задача №3Вкладчик положил в банк 50000 рублей
- 9. Задача №4Сколько лет лежал в банке вклад
- 10. *Сложный процентный рост:Банк выплачивает вкладчикам каждый месяц
- 11. * Пусть S0 - первоначальная сумма долга, i=p/100
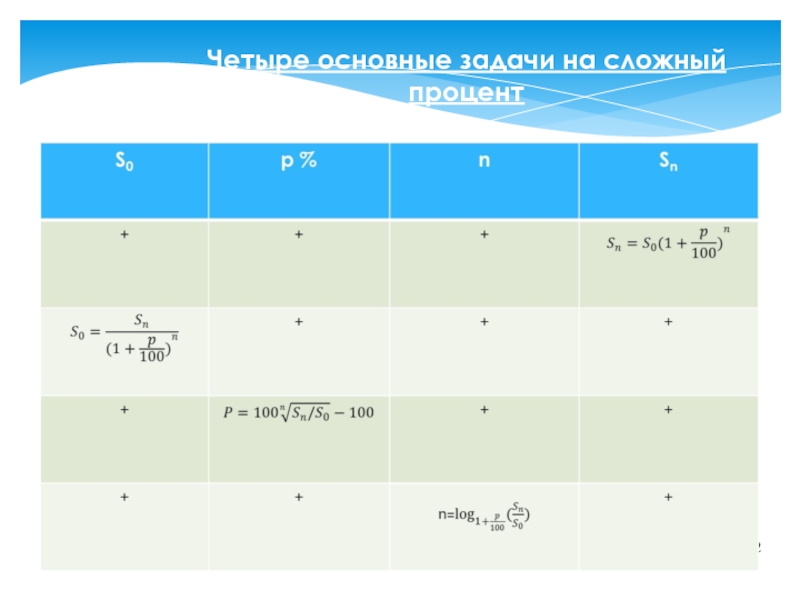
- 12. *Четыре основные задачи на сложный процент
- 13. Задача №1За хранение денег банк начисляет вкладчику
- 14. Задача №2В комиссионном магазине цена товара, выставляемого
- 15. Задача №3Рассчитайте, что выгоднее для вкладчика: получить
- 16. Формула наращения по сложным процентам, когда ставка
- 17. Пример : В договоре зафиксирована переменная ставка сложных
- 18. Благодарю за внимание!
Слайд 1Решение задач на простые и сложные проценты с помощью
MS Excel
Выполнила:
Учитель
Славинская Галина Николаевна
Слайд 3 Под наращенной суммой ссуды (долга, депозита, других видов инвестированных
Пусть S0 первоначальная сумма денег, i =p/100 ставка простых процентов.
Процесс изменения суммы долга с начисленными простыми процентами описывается арифметической прогрессией, членами которой являются величины
S0; S0+S0*i=S0(1+i) и т.д. до S0(1+ni)
Формула наращения по простым процентам
Слайд 4 Первый член этой прогрессии равен S0, разность S0*i, а последний член
S=S0(1+ni), (1)
и является наращенной суммой. Формула (1) называется формулой наращения по простым процентам или, кратко, формулой простых процентов. Множитель (1+ni) является множителем наращения. Он показывает во сколько раз наращенная сумма больше первоначальной суммы. Наращенную сумму можно представить в виде двух слагаемых: первоначальной суммы S0 и суммы процентов I
S=S0+I, (2)
где
I=S0ni. (3)
Рис. 1. Наращение по простой процентной ставке
Процесс роста суммы долга по простым процентам легко представить графически (см. Рис. 1). При начислении простых процентов по ставке i за базу берется первоначальная сумма долга. Наращенная сумма S растет линейно от времени.
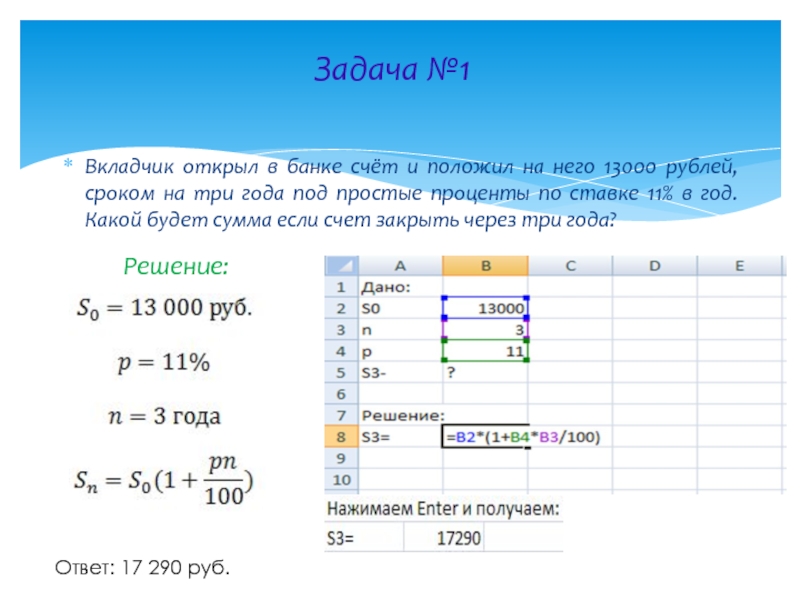
Слайд 6Задача №1
Вкладчик открыл в банке счёт и положил на него 13000
Решение:
Ответ: 17 290 руб.
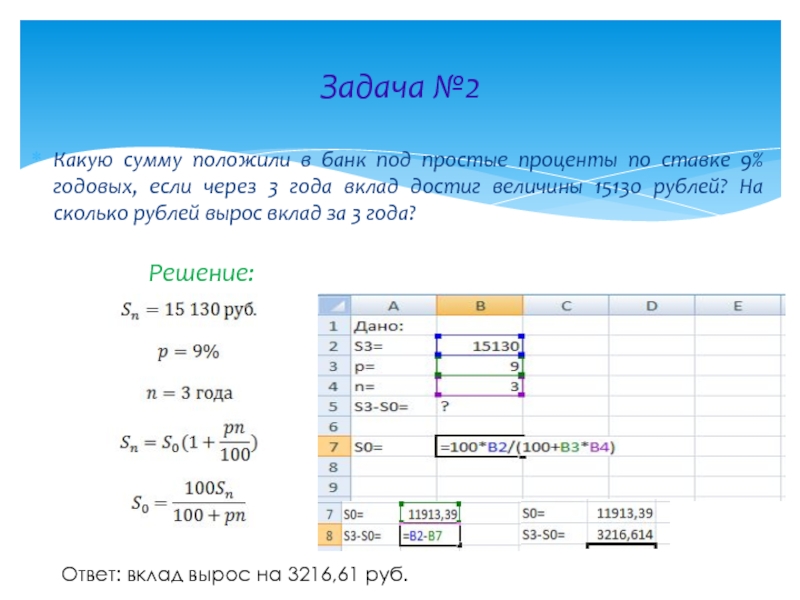
Слайд 7Задача №2
Какую сумму положили в банк под простые проценты по ставке
Решение:
Ответ: вклад вырос на 3216,61 руб.
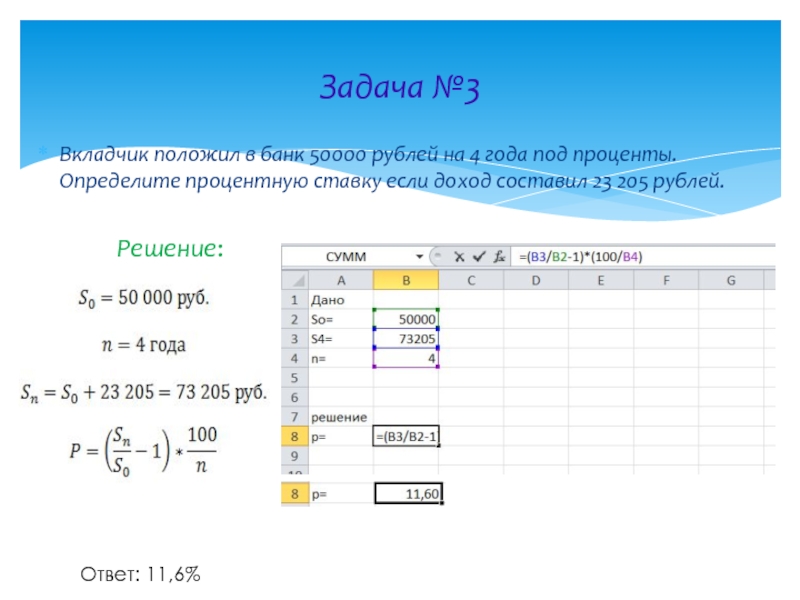
Слайд 8Задача №3
Вкладчик положил в банк 50000 рублей на 4 года под
Решение:
Ответ: 11,6%
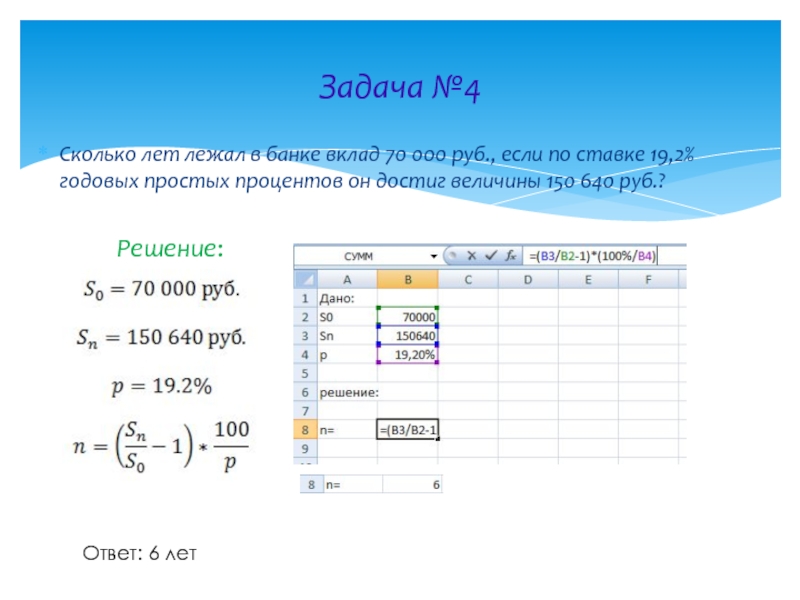
Слайд 9Задача №4
Сколько лет лежал в банке вклад 70 000 руб., если
Решение:
Ответ: 6 лет
Слайд 10*
Сложный процентный рост:
Банк выплачивает вкладчикам каждый месяц p % от имеющейся
счёте суммы, если вкладчик не снимает проценты.
S0 – первоначальный взнос.
Через n месяцев на счёте окажется
Слайд 11*
Пусть S0 - первоначальная сумма долга, i=p/100 – cтавка сложных %.
Тогда через один год сумма долга с присоединенными процентами составит S0(1+i), через 2 года S0(1+i)(1+i)= S0(1+i)2, через n лет — S0(1+i)n.
Таким образом, получаем формулу наращения для сложных процентов:
S= S0(1+i)n
где S — наращенная сумма, i — годовая ставка сложных процентов, n — срок ссуды, (1+i)n — множитель наращения.
Наращение по сложным процентам представляет собой рост по закону геометрической прогрессии, первый член которой равен S0, а знаменатель (1+i).
Формула наращения по сложным процентам
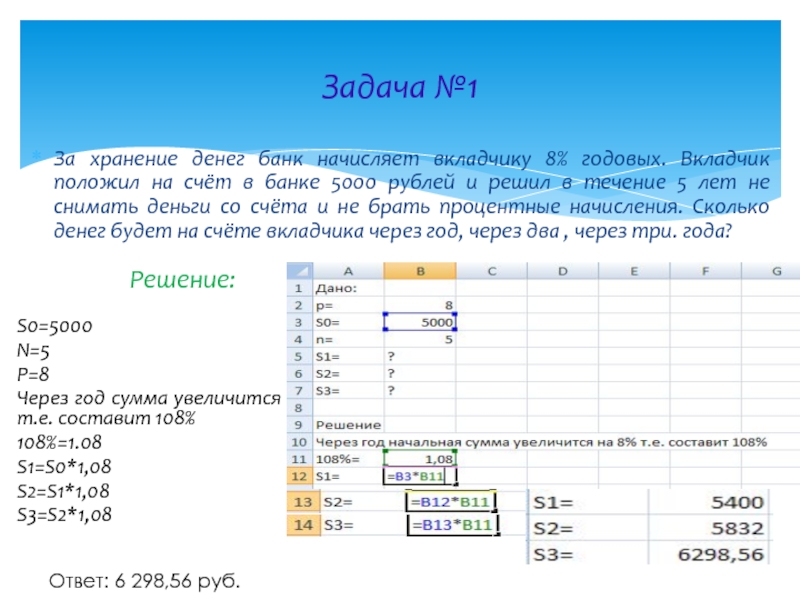
Слайд 13Задача №1
За хранение денег банк начисляет вкладчику 8% годовых. Вкладчик положил
Решение:
S0=5000
N=5
P=8
Через год сумма увеличится на 8% т.е. составит 108%
108%=1.08
S1=S0*1,08
S2=S1*1,08
S3=S2*1,08
Ответ: 6 298,56 руб.
Слайд 14Задача №2
В комиссионном магазине цена товара, выставляемого на продажу , ежемесячно
Решение:
S0=8000
n=3
S3=4096
X- количество процентов, на которое ежемесячно уменьшалась цена товара
X=100-((S3/S0)^(1/n))*100
Ответ: на 20 %.
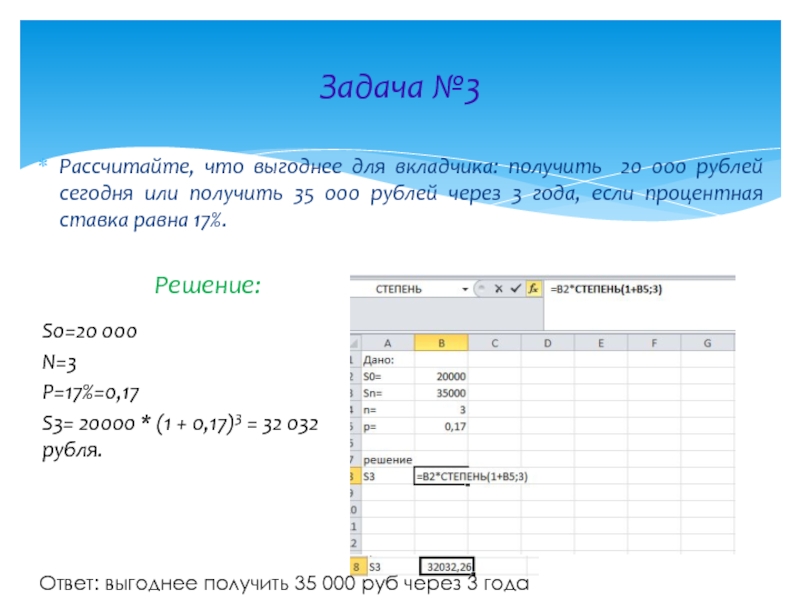
Слайд 15Задача №3
Рассчитайте, что выгоднее для вкладчика: получить 20 000 рублей сегодня
Решение:
S0=20 000
N=3
P=17%=0,17
S3= 20000 * (1 + 0,17)3 = 32 032 рубля.
Ответ: выгоднее получить 35 000 руб через 3 года
Слайд 16Формула наращения по сложным процентам, когда ставка меняется во времени
В том
где i1, i2,..., ik — последовательные значения ставок процентов, действующих в периоды n1, n2,..., nk соответственно, P- первоначальный взнос.
Слайд 17Пример :
В договоре зафиксирована переменная ставка сложных процентов, определяемая как 20%
Решение:
(1+0,3)2(1+0,28)(1+0,25)=2,704