- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Решение логарифмических неравенств
Содержание
- 1. Презентация по математике на тему Решение логарифмических неравенств
- 2. Решение неравенств Определение и свойства логарифмаЛогарифмическая функция,
- 3. Задания для повторения№ 1Преобразуйте выражения, используя свойства логарифмов
- 4. Задания для повторения№ 2Представьте число в виде логарифма с основанием 2Вычислите:№ 3
- 5. Задания для повторения№ 4Выясните, при каких значениях Х существует логарифм
- 6. Решение простейших логарифмических неравенствмонотонность логарифмической функциивозрастаетне меняемубывает меняем
- 7. Решите неравенстваПереход к равносильной системеСвойства логарифмаСвойства логарифмической
- 8. Проверка165
- 9. Проверка4,755
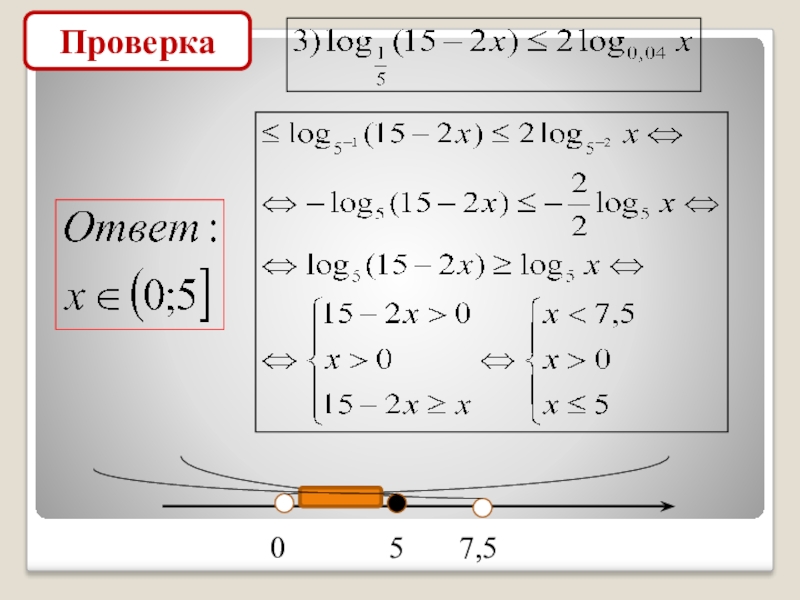
- 10. Проверка07,55
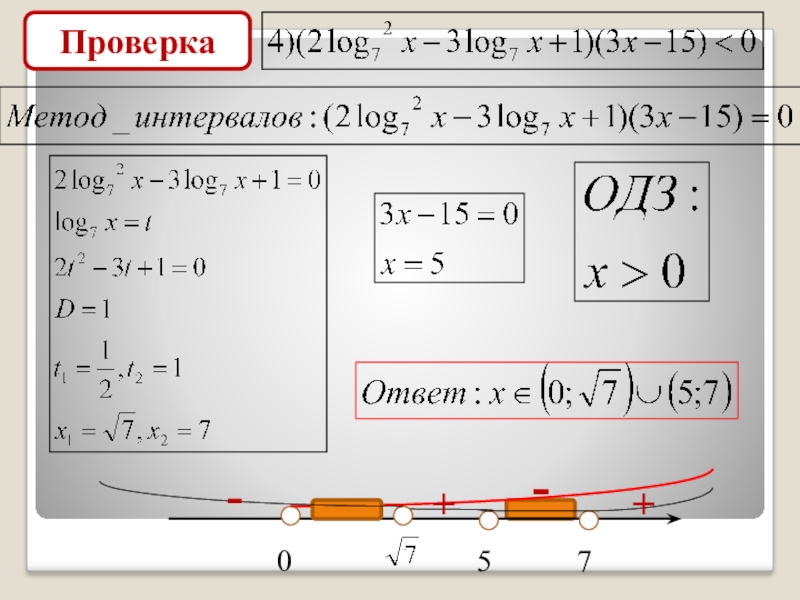
- 11. Проверка057-+-+
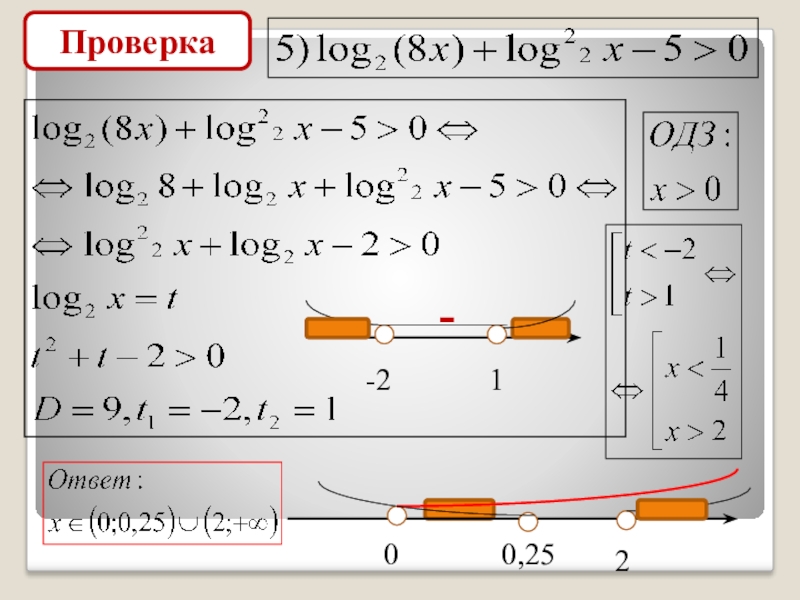
- 12. Проверка00,252-21-
- 13. Мастер-классПлан решения: к основанию 5 в левую
- 14. Теорема: выражения log а b и (b
- 15. Теорема: выражения log а b и (b
- 16. План решения: ОДЗ выполнить замену логарифмов на
- 17. «3» 25-49«4» 50-75«5» 76-90
- 18. Домашнее заданиеНа следующих занятиях мы продолжим знакомиться с рациональными методами решения неравенствКакие цели урока выполнили?
Слайд 1Разработка учителя математики
высшей квалификационной категории
Мишхожевой Л.Х.
Тема: «Решение логарифмических неравенств»
Цели:
повторить теоретический материал;
выполнить практическую работу, вспомнить методы решения логарифмических неравенств;
научиться находить рациональные способы решения;
строить алгоритм решения неравенства;
распределять время для выполнения работы;
правильно оформлять работу;
выработать волевую саморегуляцию (умение мобилизировать себя на решение проблемы).
Слайд 2Решение неравенств
Определение и свойства логарифма
Логарифмическая функция, её свойства и график
Равносильные
Основные виды неравенств и способы их решения
Методы решения неравенств
Слайд 6
Решение простейших логарифмических неравенств
монотонность логарифмической функции
возрастает
не меняем
убывает
меняем
Слайд 7Решите неравенства
Переход к равносильной системе
Свойства логарифма
Свойства логарифмической функции
Метод интервалов
Метод подстановки
?
Работа
Решите неравенства самостоятельно
Слайд 13Мастер-класс
План решения:
к основанию 5
в левую часть
разность квадратов
произведение двух логарифмов > 0
метод интервалов
расщепление неравенства
другой способ
Теорема: выражения log а b и (b – 1)(а – 1) имеют одинаковые знаки на ОДЗ логарифма
План решения:
к основанию 5
в левую часть
разность квадратов
произведение суммы и разности двух логарифмов
произведение двух логарифмов > 0
метод интервалов
расщепление неравенства
другой способ –
метод рационализации
Слайд 14Теорема: выражения log а b и (b – 1)(а – 1)
Доказательство
Пусть
Слайд 15Теорема: выражения log а b и (b – 1)(а – 1)
Вывод: в решении неравенства мы можем заменить
учитывая ОДЗ логарифма, если
в правой части нуль;
в левой части логарифм или произведение (частное) с логарифмом.
Решите неравенства новым рациональным способом:
Слайд 16План решения:
ОДЗ
выполнить замену логарифмов на (a-1)(b-1)
решить неравенство методом
записать ответ с учётом ОДЗ.
Слайд 18Домашнее задание
На следующих занятиях мы продолжим знакомиться с рациональными методами решения
Какие цели урока выполнили?