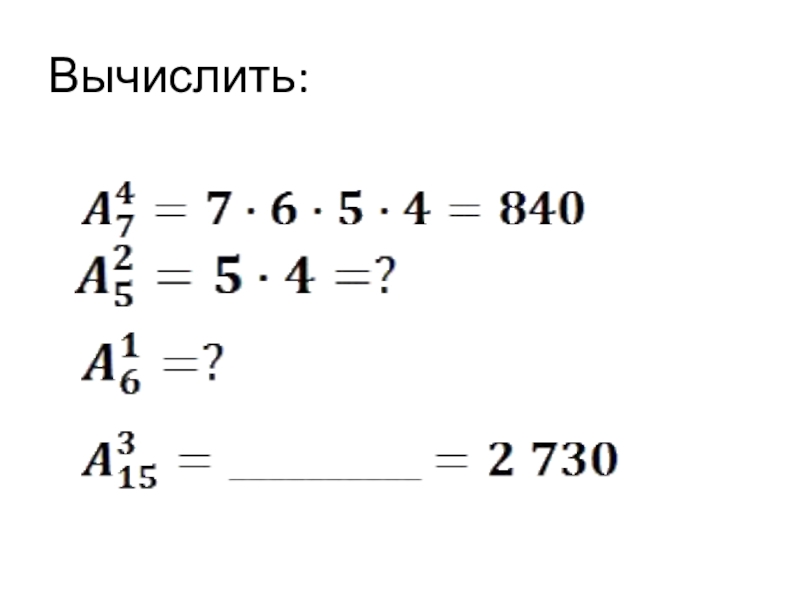- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Размещения без повторений
Содержание
- 1. Презентация по математике на тему Размещения без повторений
- 2. Историческая справка Задачи, связанные
- 3. Научными исследованиями по комбинаторике занималисьДж. Кардано (1501
- 4. Комбинаторика- раздел математики, в котором изучаются различные
- 5. Правило произведенияЕсли существует n вариантов выбора первого
- 6. Задача 1. Сколько различных двузначных чисел можно
- 7. Соединением называется каждое конкретное подмножество, составленное из элементов данного множестваВиды соединенийРазмещения ПерестановкиСочетания
- 8. Размещения без повторенийРазмещениями из m элементов по
- 9. Задача 1. Сколько различных двузначных чисел можно
- 10. Формула для нахождения числа размещений без повторенийили
- 11. Задача. Сколькими способами можно обозначить вершины данного
- 12. Задача на размещенияЗадача 1. Сколькими способами можно
- 13. Вычислить:
- 14. ЗадачаСколькими способами могут быть распределены первая, вторая и третья премии между 15 участниками конкурса?
- 15. ЗадачаНа странице альбома 6 свободных мест для
Слайд 2Историческая справка
Задачи, связанные
Слайд 3Научными исследованиями по комбинаторике занимались
Дж. Кардано (1501 – 1576),
Н. Тарталья (около
Г. Галилей (1564 – 1642),
Б. Паскаль (1623 – 1662),
П. Ферма (1601 – 1665),
Г.Лейбниц (1646 – 1716),
Л.Эйлер ( 1707 – 1783).
Слайд 4Комбинаторика
- раздел математики, в котором изучаются различные вопросы, связанные
Слайд 5Правило произведения
Если существует n вариантов выбора первого элемента и для каждого
Слайд 6Задача 1. Сколько различных двузначных чисел можно записать с помощью цифр
В качестве первой цифры числа может быть выбрана любая из цифр 2, 4, 6, 8 (n = 4). Второй цифрой может служить любая из данных цифр 0, 2, 4, 6, 8 (m = 5). Согласно правилу произведения число всевозможных двузначных чисел, составленных из предложенных цифр, равно n m = 4 5 = 20.
Слайд 7Соединением называется каждое конкретное подмножество, составленное из элементов данного множества
Виды соединений
Размещения
Перестановки
Сочетания
Слайд 8Размещения без повторений
Размещениями из m элементов по n элементов (n m)
Слайд 9Задача 1. Сколько различных двузначных чисел можно записать с помощью цифр
Перебором убедимся в том, что из четырёх цифр 1, 2, 3, 4 можно составить 12 двузначных чисел, удовлетворяющих условию задачи: 12, 13, 14, 21, 23, 24, 31, 32, 34, 41, 42, 43. По правилу произведения таких двузначных чисел 12. На первом месте может стоять любая из данных четырёх цифр, а на втором месте – любая из трёх оставшихся.
Слайд 11Задача. Сколькими способами можно обозначить вершины данного треугольника, используя буквы A,
Решение задачи сводится к нахождению числа размещений из 6 элементов по 3 элемента в каждом. По формуле для нахождения числа размещений без повторений находим
то есть вершины можно обозначить 120 способами.
Слайд 12Задача на размещения
Задача 1. Сколькими способами можно выбрать из класса, насчитывающего
Решение.
Слайд 14Задача
Сколькими способами могут быть распределены первая, вторая и третья премии между
Слайд 15Задача
На странице альбома 6 свободных мест для фотографий.
Сколькими способами можно
Решение: