- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Прямоугольная система координат
Содержание
- 1. Презентация по математике на тему Прямоугольная система координат
- 2. Вы уже знакомы с прямоугольной (Декартовой) системой
- 3. А, вот, прямоугольную систему координат в пространстве ввёл швейцарский, немецкий, российский математик Леонард Эйлер в XVIIIв.
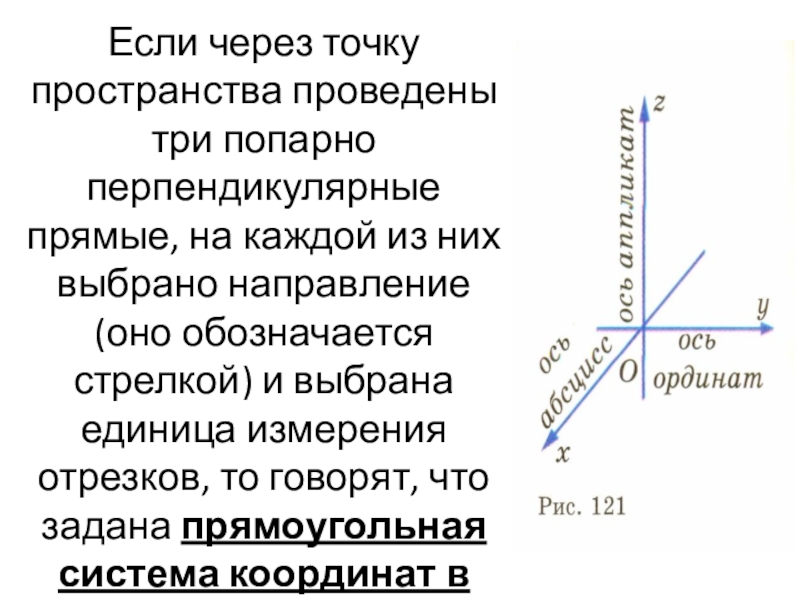
- 4. Если через точку пространства проведены три попарно
- 5. Прямые с выбранными на них направлениями называются
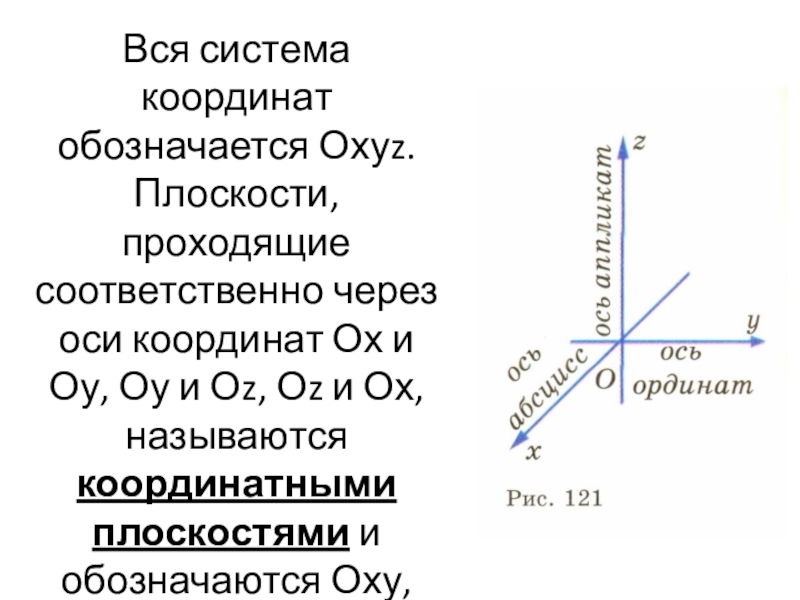
- 6. Вся система координат обозначается Охуz. Плоскости, проходящие
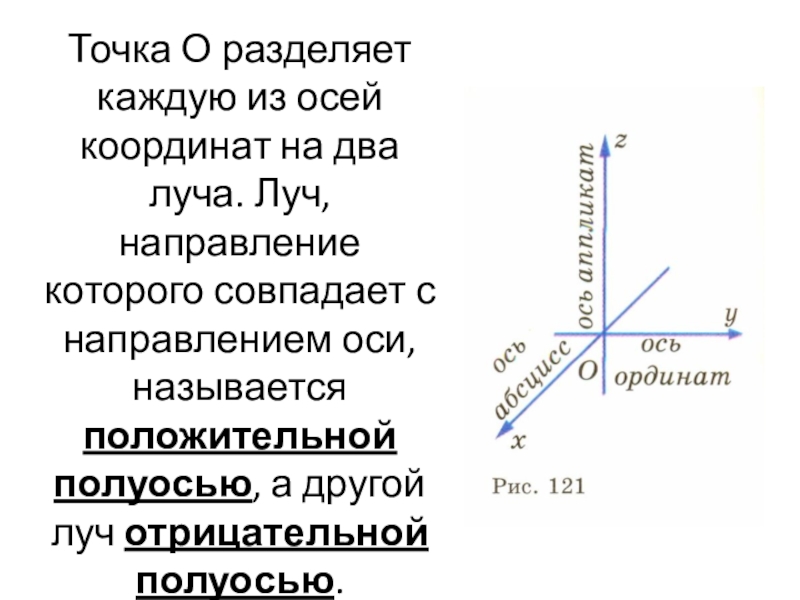
- 7. Точка О разделяет каждую из осей координат
- 8. И так:Выбрать точку пространстваПровести через неё 3
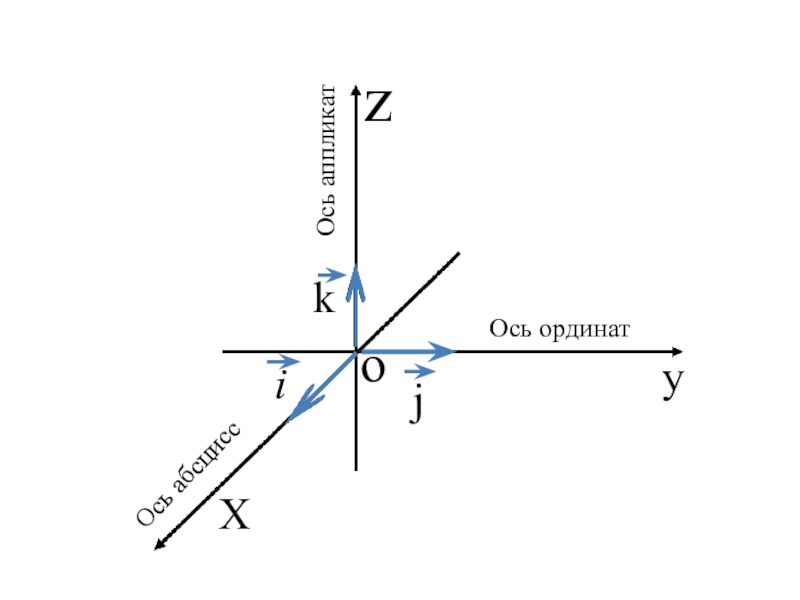
- 9. Ось абсциссОсь ординатОсь аппликат
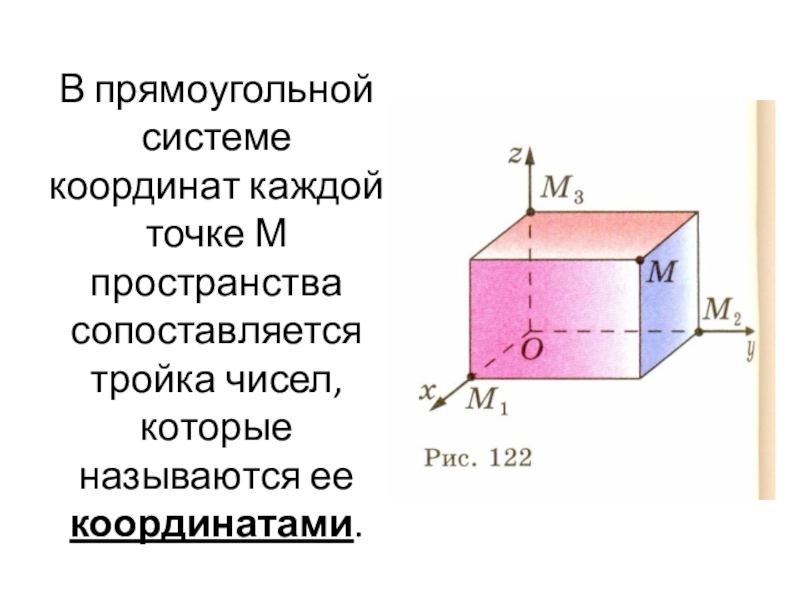
- 10. В прямоугольной системе координат каждой точке М пространства сопоставляется тройка чисел, которые называются ее координатами.
- 11. И так:- Чтобы определить координаты токи в пространстве, надо через точку провести плоскости параллельно осям.
- 12. Если М ОХУ, то
- 13. На рисунке изображены шесть точек А (9;
- 14. Закрепление № 400№401 а№ 402
- 15. №400Ответ:а) С(2;0;0)б) Е(0;-1;0)В) В(0;0;-7)г) А(3;-1;0)д) G(0;5;-7)е) D (-4 ;0;3)
- 16. №401(a)Ответ:а) A1(2;0;5), B1(3;0;1/2), C1 (-
- 17. №402Дано: А(0;0;0)
- 18. Домашнее заданиеп.46, №401(б)
- 19. Координаты вектора
- 20. Любой вектор a и можно разложить по
- 21. Коэффициенты х, у и z в разложении
- 22. Рассмотрим правила, которые позволяют по координатам данных
- 23. 10. Каждая координата суммы двух или более
- 24. 20. Каждая координата разности двух векторов равна
- 25. 30. Каждая координата произведения вектора на число
Вы уже знакомы с прямоугольной (Декартовой) системой координат на плоскости, которую в XIX в. ввёлфранцузский математикРене Декарт
Слайд 2Вы уже знакомы с прямоугольной (Декартовой) системой координат на плоскости, которую
в XIX в. ввёл
французский
математик
Рене Декарт
Слайд 3А, вот, прямоугольную систему координат в пространстве ввёл швейцарский,
немецкий,
российский
математик
Леонард Эйлер
в XVIIIв.
Слайд 4Если через точку пространства проведены три попарно перпендикулярные прямые, на каждой
из них выбрано направление (оно обозначается стрелкой) и выбрана единица измерения отрезков, то говорят, что задана прямоугольная система координат в пространстве
Слайд 5Прямые с выбранными на них направлениями называются осями координат, а их
общая точка — началом координат. Она обозначается обычно буквой О. Оси координат обозначаются так: Ох, Оу, Оz — и имеют названия: ось абсцисс, ось ординат, ось аппликат.
Слайд 6Вся система координат обозначается Охуz. Плоскости, проходящие соответственно через оси координат
Ох и Оу, Оу и Оz, Оz и Ох, называются координатными плоскостями и обозначаются Оху, Оуz, Оzх.
Слайд 7Точка О разделяет каждую из осей координат на два луча. Луч,
направление которого совпадает с направлением оси, называется положительной полуосью, а другой луч отрицательной полуосью.
Слайд 8И так:
Выбрать точку пространства
Провести через неё 3 попарно перпендикулярные прямые
Указать стрелкой
направление
На каждой оси выбрать единицу измерения
На каждой оси выбрать единицу измерения
(строим на доске и в тетради)
Слайд 10В прямоугольной системе координат каждой точке М пространства сопоставляется тройка чисел,
которые называются ее координатами.
Слайд 11И так:
- Чтобы определить координаты токи в пространстве, надо через точку
провести плоскости параллельно осям.
Слайд 12Если М ОХУ, то z=0
Если М
OXZ, то у=0
Если М OУZ, то X=0
Если М ОХ, то У=0 и Z=0
Если М OУ, то Х=0 и Z=0
Если М OZ, то Х=0 и У=0
Если М OУZ, то X=0
Если М ОХ, то У=0 и Z=0
Если М OУ, то Х=0 и Z=0
Если М OZ, то Х=0 и У=0
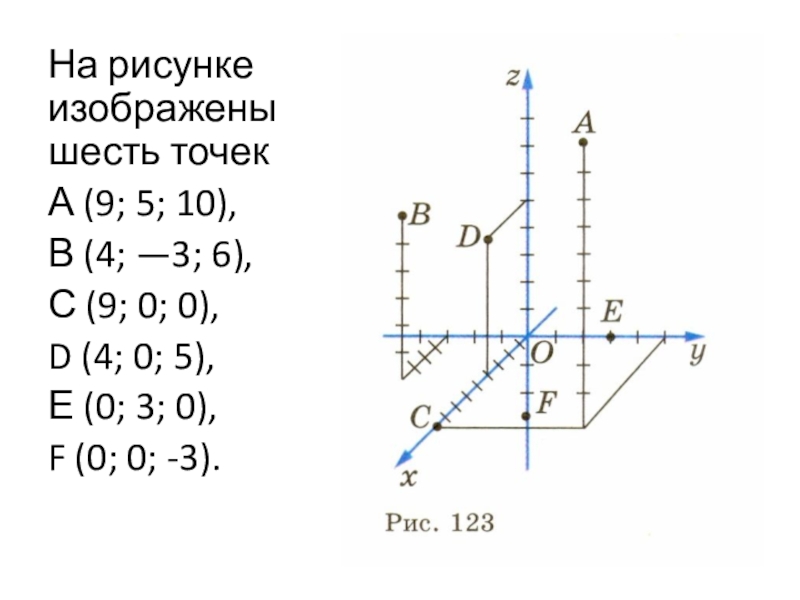
Слайд 13На рисунке изображены шесть точек
А (9; 5; 10),
В (4;
—3; 6),
С (9; 0; 0),
D (4; 0; 5),
Е (0; 3; 0),
F (0; 0; -3).
С (9; 0; 0),
D (4; 0; 5),
Е (0; 3; 0),
F (0; 0; -3).
Слайд 16№401(a)
Ответ:
а) A1(2;0;5), B1(3;0;1/2), C1 (- ;0;
- )
A2(2;-3;0), B2(3-5;0),C2(- ;- /2;0)
A3 (0;-3;5),B3(0;-5;1/2), C3(- ; - /2;0)
A2(2;-3;0), B2(3-5;0),C2(- ;- /2;0)
A3 (0;-3;5),B3(0;-5;1/2), C3(- ; - /2;0)
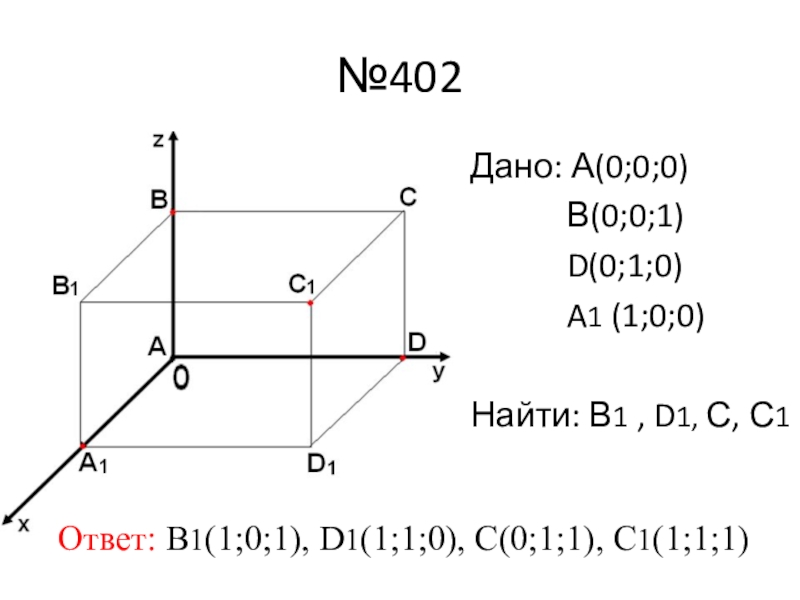
Слайд 17№402
Дано: А(0;0;0)
В(0;0;1)
D(0;1;0)
A1 (1;0;0)
Найти: В1 , D1, С, С1
A1 (1;0;0)
Найти: В1 , D1, С, С1
Ответ: В1(1;0;1), D1(1;1;0), С(0;1;1), С1(1;1;1)
Слайд 20Любой вектор a и можно разложить по координатным векторам, т. е.
представить в виде
причем коэффициенты разложения х, у, z определяются единственным образом.
Слайд 21Коэффициенты х, у и z в разложении вектора a по координатным
векторам называются координатами вектора a в данной системе координат.
Слайд 22Рассмотрим правила, которые позволяют по координатам данных векторов найти координаты их
суммы и разности, а также координаты произведения данного вектора на данное число.
Слайд 2310. Каждая координата суммы двух или более векторов равна сумме соответствующих
координат этих векторов. Другими словами, если
a {х1, у1, z1} и b{х2, у2, z2} — данные векторы, то вектор a+b имеет координаты
{х1+х2, у1 + у2, z1 + z2}.
Слайд 2420. Каждая координата разности двух векторов равна разности соответствующих координат этих
векторов. Другими словами, если
a {х1, y1, z1} и b{х2 у2; z2} — данные векторы, то вектор a— b имеет координаты
{х1- х2, y1 – y2, z1 - z2}.
Слайд 2530. Каждая координата произведения вектора на число равна произведению соответствующей координаты
вектора на это число.
Другими словами, если
а {х; у; х} — данный вектор, α — данное число, то вектор αa имеет координаты {αх; αу; αz).