- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Призма. Пирамида. Решение задач
Содержание
- 1. Презентация по математике на тему Призма. Пирамида. Решение задач
- 2. ОСНОВАНИЕМ ПРЯМОЙ ТРЕУГОЛЬНОЙ ПРИЗМЫ СЛУЖИТ ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК
- 3. 1200А1
- 4. В прямоугольном параллелепипеде стороны основания равны 12
- 5. В правильной треугольной призме ABCA1B1C1, все ребра
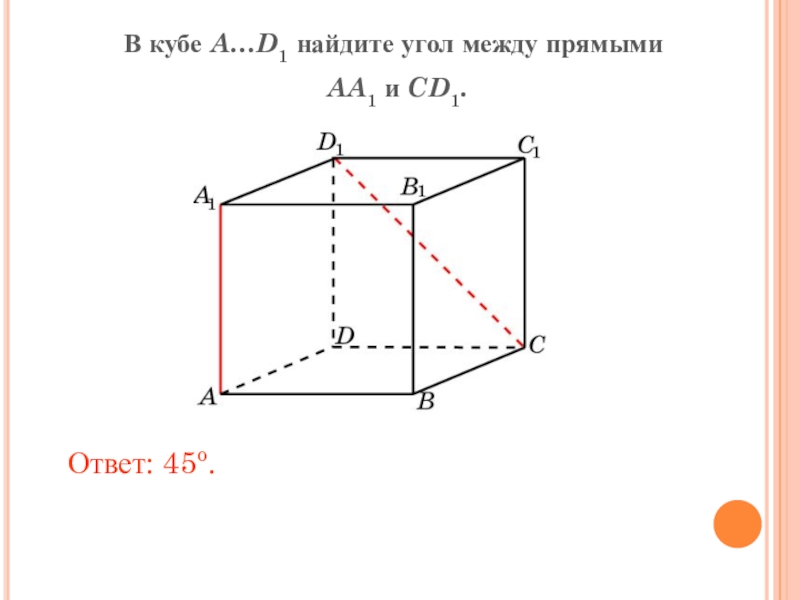
- 6. В кубе A…D1 найдите угол между прямыми AA1 и CD1.Ответ: 45o.
- 7. В правильной треугольной призме ABCA1B1C1, все ребра
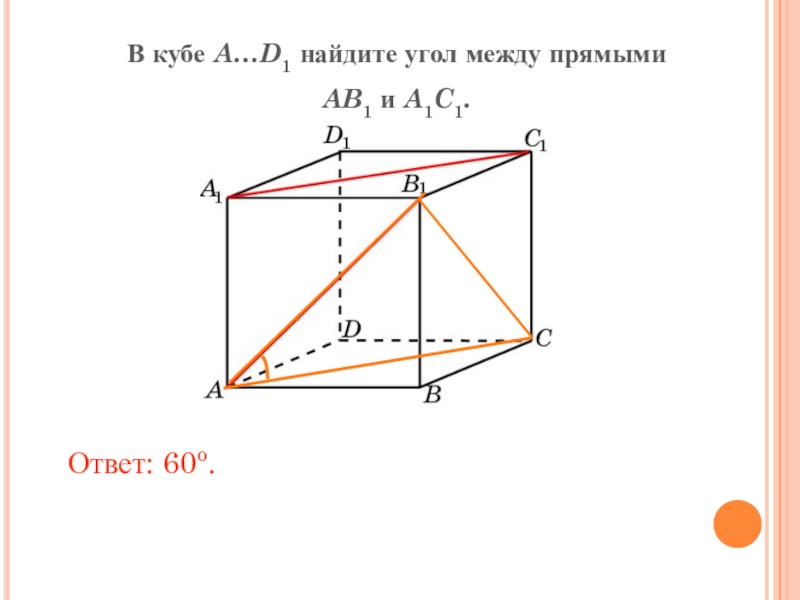
- 8. В кубе A…D1 найдите угол между прямыми AB1 и A1C1.Ответ: 60o.
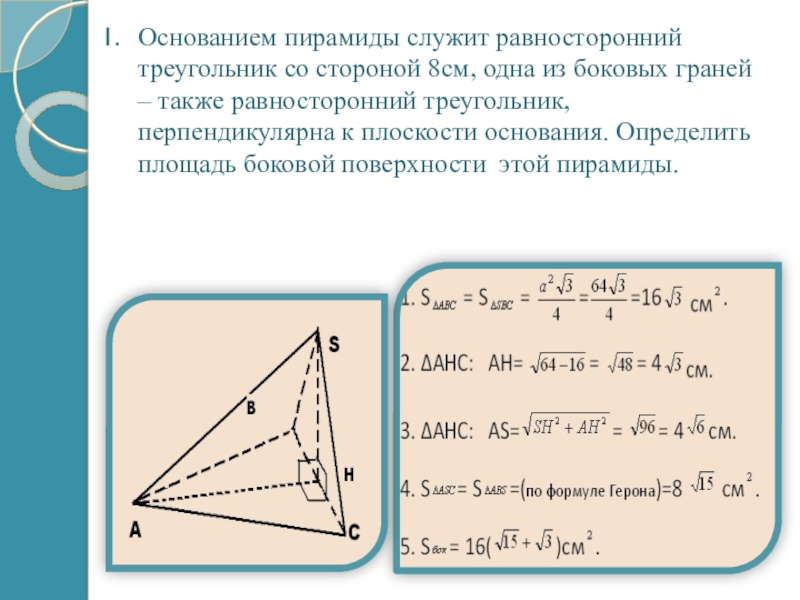
- 9. Основанием пирамиды служит равносторонний треугольник со стороной
- 10. 2. Три смежных ребра треугольной пирамиды попарно
- 11. 3. Основание пирамиды- прямоугольник со сторонами 6см
- 12. 4. Основание пирамиды – прямоугольный треугольник с
- 13. 5. Основанием пирамиды служит треугольник со сторонами
ОСНОВАНИЕМ ПРЯМОЙ ТРЕУГОЛЬНОЙ ПРИЗМЫ СЛУЖИТ ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК С КАТЕТАМИ 3 И 4, ВЫСОТА ПРИЗМЫ РАВНА 6. НАЙДИТЕ:
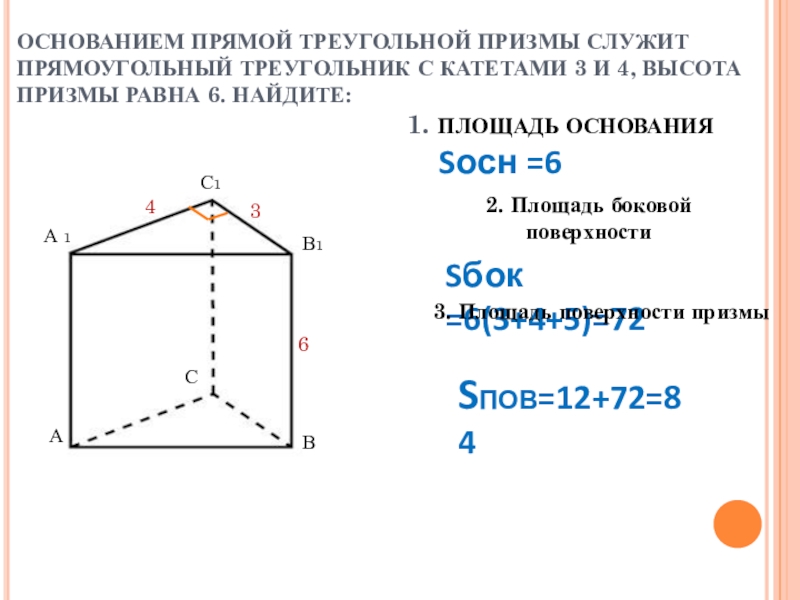
Слайд 2ОСНОВАНИЕМ ПРЯМОЙ ТРЕУГОЛЬНОЙ ПРИЗМЫ СЛУЖИТ ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК С КАТЕТАМИ 3 И
4, ВЫСОТА ПРИЗМЫ РАВНА 6. НАЙДИТЕ:
1. ПЛОЩАДЬ ОСНОВАНИЯ
3
4
6
А
С
В
А 1
С1
В1
Sосн =6
Sбок =6(3+4+5)=72
2. Площадь боковой поверхности
3. Площадь поверхности призмы
SПОВ=12+72=84
Слайд 31200
А1
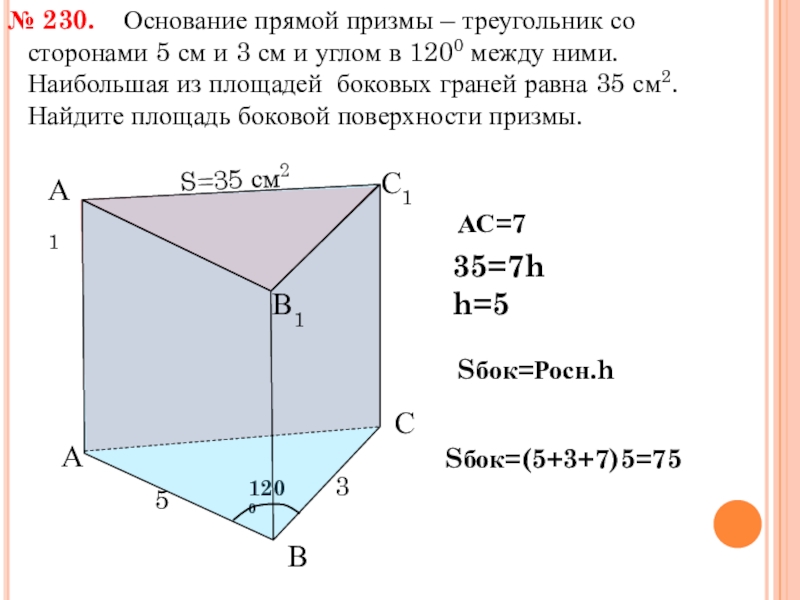
Основание прямой призмы –
треугольник со сторонами 5 см и 3 см и углом в 1200 между ними. Наибольшая из площадей боковых граней равна 35 см2. Найдите площадь боковой поверхности призмы.
№ 230.
А
В
С
С1
В1
3
5
S=35 см2
АС=7
35=7h
h=5
Sбок=Росн.h
Sбок=(5+3+7)5=75
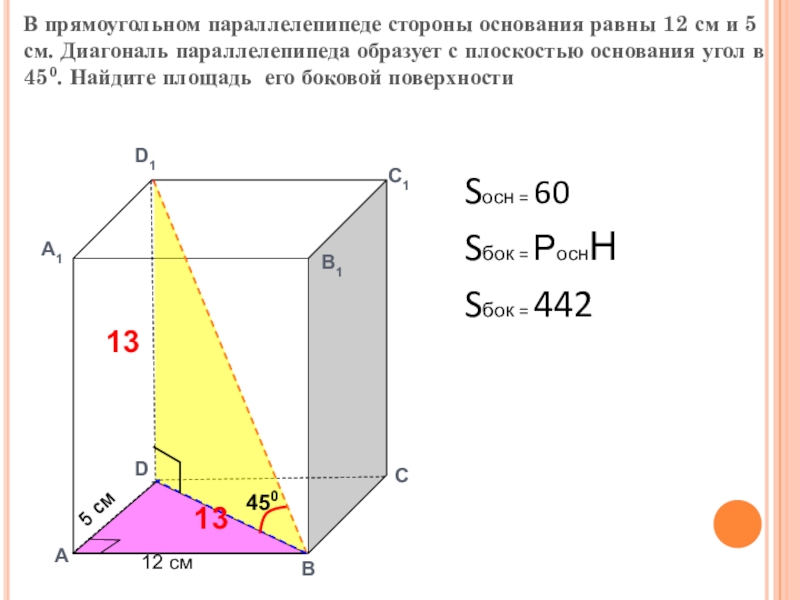
Слайд 4В прямоугольном параллелепипеде стороны основания равны 12 см и 5 см.
Диагональ параллелепипеда образует с плоскостью основания угол в 450. Найдите площадь его боковой поверхности
В
С
А1
D1
С1
В1
13
D
А
12 см
5 см
13
Sосн = 60
Sбок = РоснН
Sбок = 442
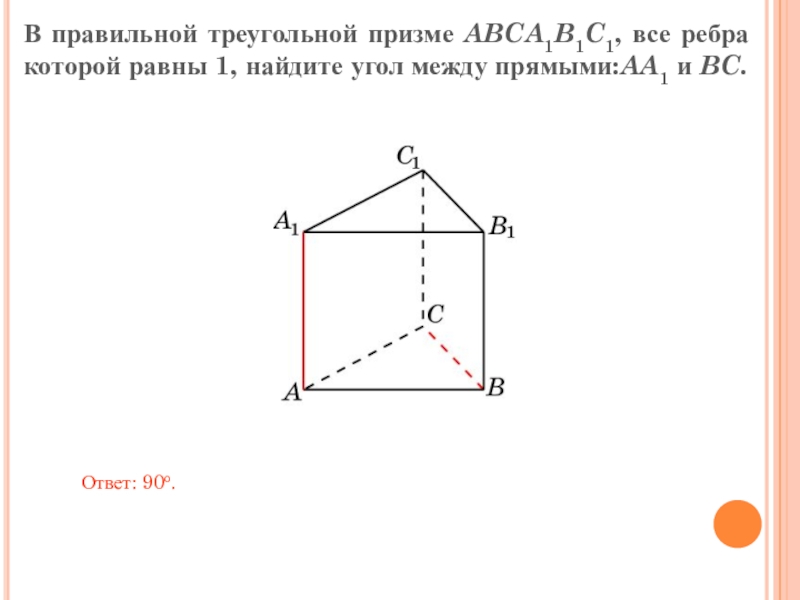
Слайд 5В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, найдите
угол между прямыми:AA1 и BC.
Ответ: 90o.
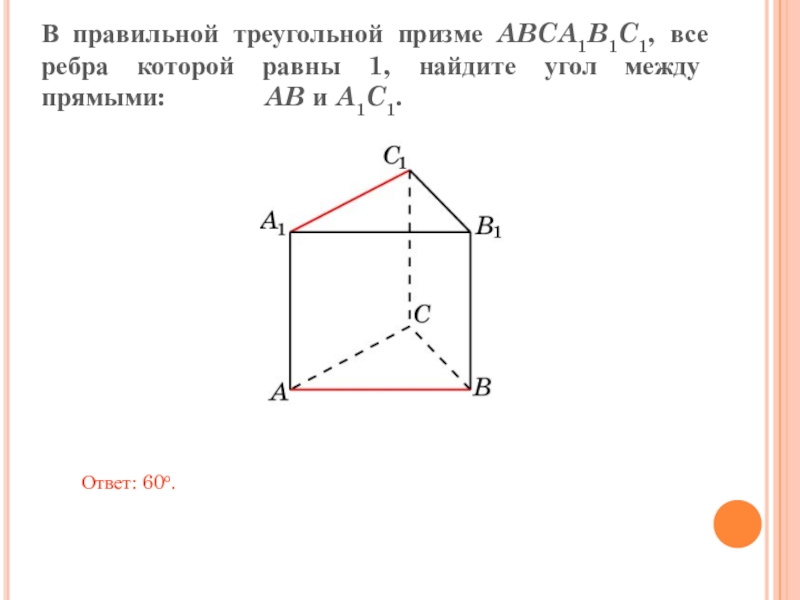
Слайд 7В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, найдите
угол между прямыми: AB и A1C1.
Ответ: 60o.
Слайд 9Основанием пирамиды служит равносторонний треугольник со стороной 8см, одна из боковых
граней – также равносторонний треугольник, перпендикулярна к плоскости основания. Определить площадь боковой поверхности этой пирамиды.
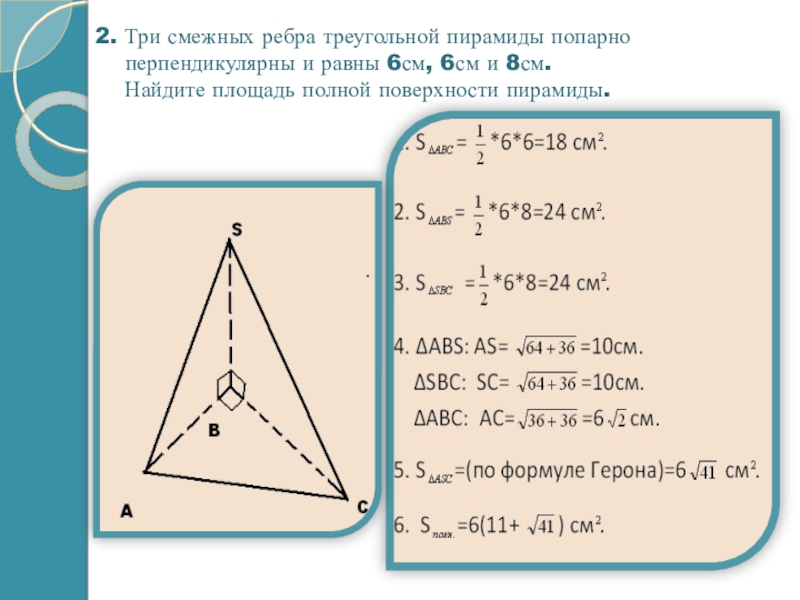
Слайд 102. Три смежных ребра треугольной пирамиды попарно перпендикулярны и равны 6см,
6см и 8см.
Найдите площадь полной поверхности пирамиды.
Найдите площадь полной поверхности пирамиды.
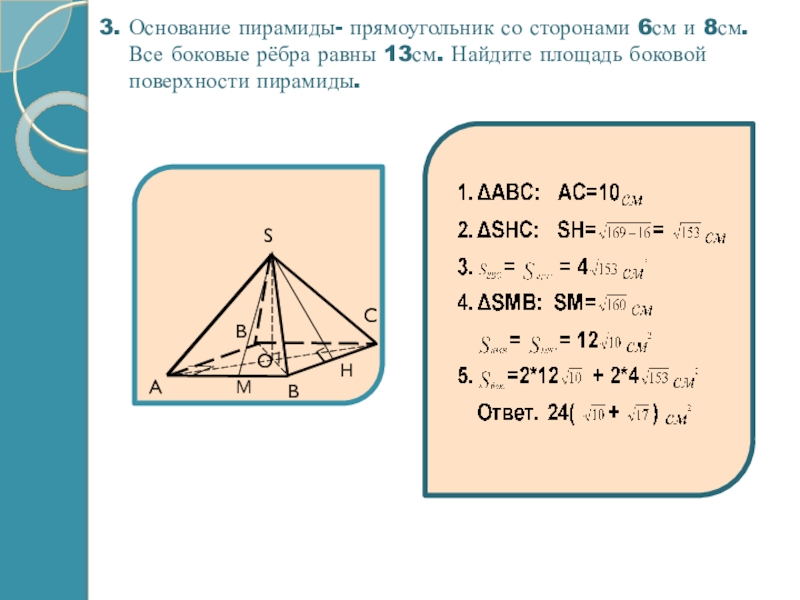
Слайд 113. Основание пирамиды- прямоугольник со сторонами 6см и 8см. Все боковые
рёбра равны 13см. Найдите площадь боковой поверхности пирамиды.
S
A
B
C
B
O
Н
М
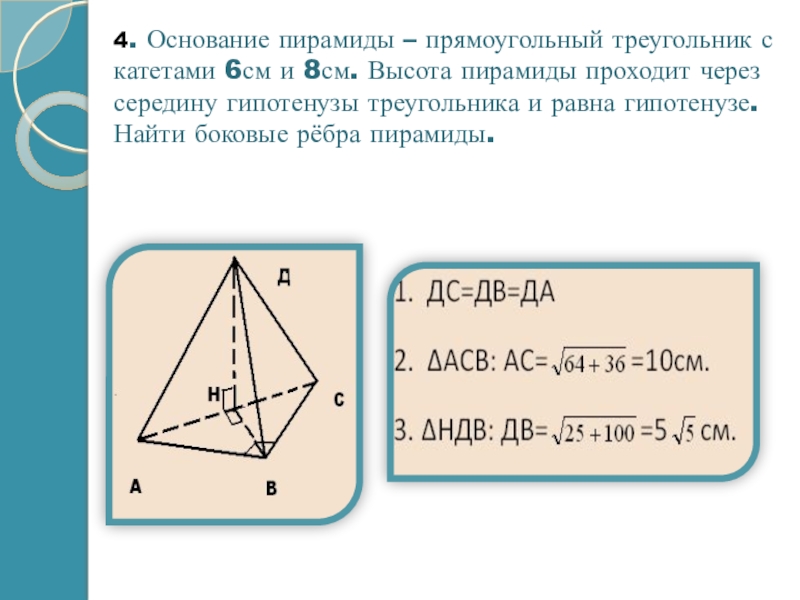
Слайд 124. Основание пирамиды – прямоугольный треугольник с катетами 6см и 8см.
Высота пирамиды проходит через середину гипотенузы треугольника и равна гипотенузе.
Найти боковые рёбра пирамиды.
Найти боковые рёбра пирамиды.
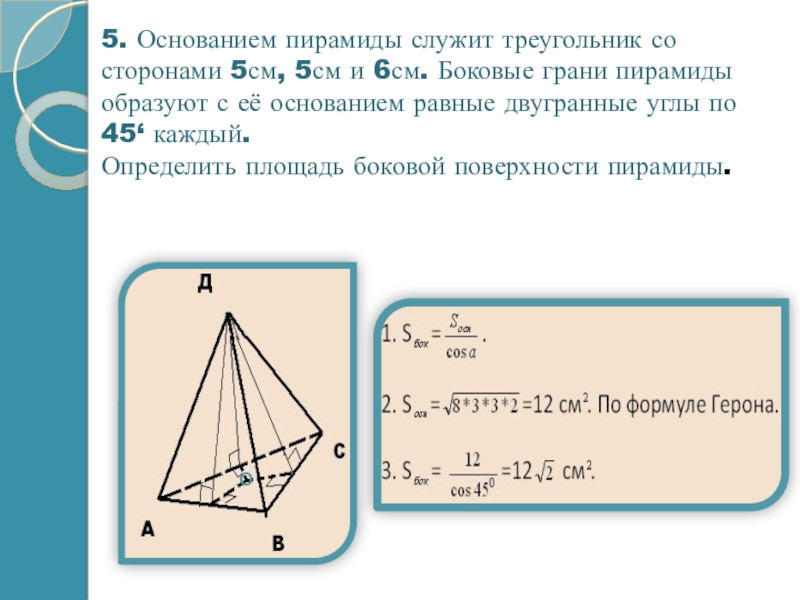
Слайд 135. Основанием пирамиды служит треугольник со сторонами 5см, 5см и 6см.
Боковые грани пирамиды образуют с её основанием равные двугранные углы по 45‘ каждый.
Определить площадь боковой поверхности пирамиды.
Определить площадь боковой поверхности пирамиды.
О
