- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Показательные уравнения и их решения (11 класс)
Содержание
- 1. Презентация по математике на тему Показательные уравнения и их решения (11 класс)
- 2. Обобщающий урок по теме «Показательные уравнения и
- 3. Ход урокаI.Организационный момент.1) Проверка готовности к уроку2)Психологический
- 4. II. Актуализация опорных знаний.Определение: показательными уравнениями называются
- 5. II. Устная работа:Найдите корень уравнения устно:
- 6. II. Устная работа:Ответы к уравнениям: 1. х=32. х=33. х=04. х=-25. х=-26. х=-37. х=-2,58. х=4
- 7. III.Диктант ( да -1, нет - 0)1
- 8. Ответ: 10100 количество верных ответов соответствует полученным баллам
- 9. III. Решение упражнений:(Первое уравнение решаем всем классом
- 10. Основные способы их решенияМетод уравнивания показателей(основан на
- 11. Разложение на множители (Основан на свойствах степеней
- 12. Показательные уравненияПримеры4 х + 1 − 2
- 13. IV.Зарабатываем баллы: 10
- 14. Вопрос 1).Какие из перечисленных функций показательные: ( 1 балл)
- 15. Вопрос 2).Какие из перечисленных функций возрастают, какие убывают ( 1 балл)
- 16. В5: а) 7 х – 2 =
- 17. Задание повышенной сложностиС5: При каком параметре а
- 18. Проверочная работа1. 0,32х + 1 = (3
- 19. VI.Задание на дом Из материалов ЕГЭ 2013
- 20. Показательные уравненияСпасибо всем за урок! УСПЕХОВ НА ЕГЭ!
Слайд 2Обобщающий урок
по теме «Показательные уравнения и их решения» Подготовка к ЕГЭ
Всякое
трудом даётся
Цель:
Повторить и обобщить материал по теме «Показательные уравнения»;
Решение показательных уравнений различных видов;
Подготовка к ЕГЭ.
Слайд 3Ход урока
I.Организационный момент.
1) Проверка готовности к уроку
2)Психологический момент.
Вопросы к классу:
Какие уравнения
Какие способы решения показательных уравнений мы знаем?
а)приведение степеней в левой и правой частях уравнения к одному основанию;
б)разложение частей уравнения на множители;
в)введение новой переменной;
г)графический способ решения;
д)деление на степень;
е)оценивание значения левой и правой частей уравнения с помощью свойств показательной функции, подбор корня.
Слайд 4II. Актуализация опорных знаний.
Определение: показательными уравнениями называются уравнения вида a
Показательное уравнение а f(x) = a g(x) (где а > 0, а 1) равносильно уравнению f(x) = g(x).
Слайд 6II. Устная работа:
Ответы к уравнениям:
1. х=3
2. х=3
3. х=0
4. х=-2
5. х=-2
6.
7. х=-2,5
8. х=4
Слайд 7III.Диктант ( да -1, нет - 0)
1 вопрос
В показательной функции показатель
2 вопрос
Если основание 0 < а < 1 , то показательная функция возрастает на своей области определения.
3 вопрос
Если основание а > 1, то знак неравенства остается без изменения
4 вопрос
При умножении степеней с одинаковыми основаниями показатели степеней умножаются
5 вопрос
Если график показательной функции преобразовали с помощью сдвига вдоль оси ОХ влево на 2 единицы, то ее область значений ( 2; + ∞ )
Слайд 9III. Решение упражнений:
(Первое уравнение решаем всем классом на доске, а второе
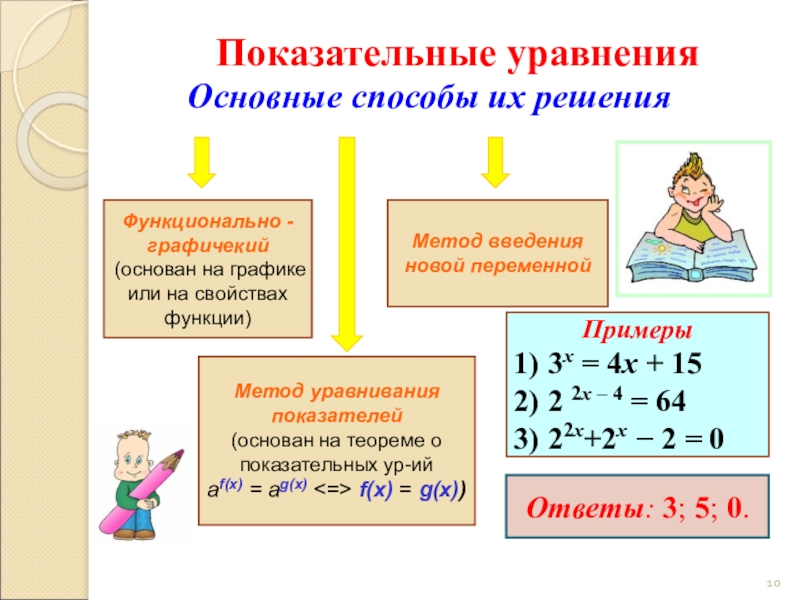
Слайд 10Основные способы их решения
Метод уравнивания показателей
(основан на теореме о показательных ур-ий
аf(x)
Метод введения новой переменной
Примеры
1) 3х = 4х + 15
2) 2 2х – 4 = 64
3) 22х+2х − 2 = 0
Функционально - графичекий (основан на графике или на свойствах функции)
Показательные уравнения
Ответы: 3; 5; 0.
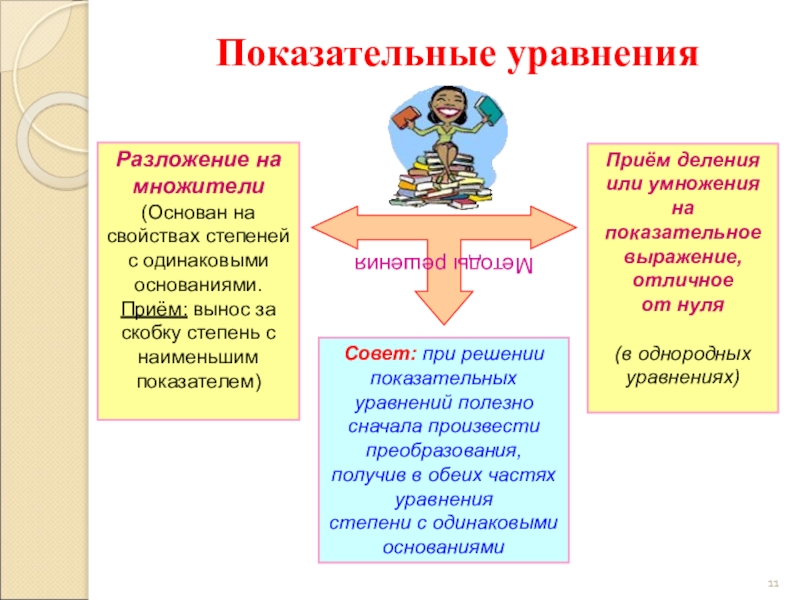
Слайд 11Разложение на множители (Основан на свойствах степеней с одинаковыми основаниями. Приём:
Приём деления или умножения
на показательное выражение, отличное
от нуля
(в однородных уравнениях)
Показательные уравнения
Совет: при решении показательных уравнений полезно сначала произвести преобразования, получив в обеих частях уравнения
степени с одинаковыми основаниями
Методы решения
Слайд 12Показательные уравнения
Примеры
4 х + 1 − 2 ∙ 4 х –
4 х – 2 ∙ (43 − 2) = 124, 4 х – 2 ∙ 62 = 124,
4 х – 2 = 2, 4 х - 2 = 40,5,…
2 ∙ 22х − 3 ∙ 2х ∙ 5х − 5 ∙ 52х = 0│
: 52х ≠ 0,
2 ∙ (2/5)2х − 3 ∙ (2/5) х − 5 = 0,
t = (2/5) х (t > 0), 2t 2 − 3 t − 5 = 0,
t = − 1, t = 5/2 (?...).
5/2 = (2/5)х,
х = 2,5
х = −1
МОЛОДЦЫ!
Слайд 13IV.Зарабатываем
баллы:
10 баллов и выше –«5»
7-9 баллов -
4-6 баллов –«3»
меньше 4 баллов –«2»
Слайд 16В5: а) 7 х – 2 = 49, б) (1/6) 12
Ответ: а) х = 4, б) х = 2.
С3: 4 х2 + 3х – 2 − 0,5 2х2 + 2х – 1= 0. (Можно 0,5 = 4– 0,5)
Решение. 4 х2 + 3х – 2 = 4 −х2 − х + 0,5
х2 + 3х – 2 = −х2 − х + 0,5, …
Ответ: х = −5/2, х = ½.
С3: 5 ∙ 5 tgy + 4 = 5 −tgy, при сosy < 0.
Указание к решению.
5 ∙ 5 tgy + 4 = 5−tgy │∙ 5 tgy ≠ 0,
5 ∙ 5 2gy + 4 ∙ 5 tgy – 1 = 0. Пусть х = 5 tgy , …
5 tgy = − 1 (?...), 5 tgy = 1/5, tgy = − 1.
Так как tgy = − 1 и сosy < 0, то у ∈ … к.ч.
у ∈ II к.ч., значит,
V.Решение заданий ЕГЭ – 2014 года
у = 3π/4 + 2πk, k ∈ N.
Слайд 17Задание повышенной сложности
С5: При каком параметре а уравнение
Решение.
Пусть t = 2х, t > 0, t 2 – 3t + (а2 – 4а) = 0 .
1) Т. к. уравнение имеет два корня, то D =…
2) Т. к. t1, 2 > 0, то t1 ∙ t2 > 0, т. е. а2 – 4а > 0 (?...).
Значит,
D > 0, −4а2 + 16а + 9 > 0,
а2 – 4а > 0; а (а − 4) > 0; …
Ответ: а ∈ (-0,5; 0) или (4; 4,5).
D > 0.
Слайд 18Проверочная работа
1. 0,32х + 1 = (3 )2
2.
у =
3. 5∙2х + 3 − 4∙2х – 1 = 19
4*. 3∙9х = 2∙15х + 5∙25х
Слайд 19VI.Задание на дом
Из материалов ЕГЭ 2013 – 2014 годов
Решить уравнения и систему уравнений:
1. (2 )х + 7 = 9/49
2. у = 3х + 2
у =
3. 2 ∙ 3х + 1 − 4 ∙ 3х – 1 = 42
4* 2 ∙ 4х − 3 ∙ 10х = 5 ∙ 25х