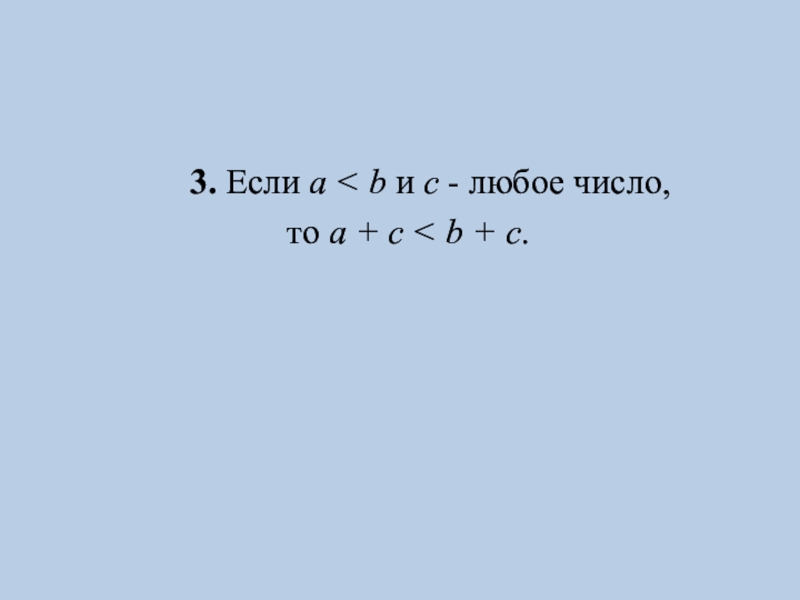Ярославль
2011
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Показательные неравенства (11 класс)
Содержание
- 1. Презентация по математике на тему Показательные неравенства (11 класс)
- 2. ПОВТОРЕНИЕ
- 3. Слайд 3
- 4. Слайд 4
- 5. 3. Если a <
- 6.
- 7. 5. Если a < b и c <
- 8. 6. Если a < b и
- 9. Решением неравенства с одной переменной
- 10. Неравенства, множества решений которых совпадают, называются равносильными.Областью
- 11. Из данного неравенства получается равносильное ему неравенство,
- 12. Из данного неравенства получается равносильное ему неравенство,
- 13. Из данного неравенства получается равносильное ему неравенство,
- 14. Определение: Показательными неравенствами называют неравенства вида a
- 15. Теорема: Показательное неравенство a f(x) > a
ПОВТОРЕНИЕ
Слайд 1Показательные неравенства
Подготовила
учитель математики МОУ лицея №86 Карпунина Елена Владимировна
Слайд 3
Число a больше числа b, если разность a - b - положительное число;
Число a меньше числа b, если разность a - b - отрицательное число;
Число a равно числу b, если разность a - b равна нулю.
Число a меньше числа b, если разность a - b - отрицательное число;
Число a равно числу b, если разность a - b равна нулю.
Слайд 4 При решении
неравенств необходимо использовать свойства числовых неравенств:
1. Если a < b, то b > a; если a > b, то b < a.
2. Если a < b и b < c, то a < c.
1. Если a < b, то b > a; если a > b, то b < a.
2. Если a < b и b < c, то a < c.
Слайд 6
4. Если a < b
и c - положительное число, то ac < bc;
если a < b и c - отрицательное число,
то ac > bc.
Следствие. Если a и b - положительные числа и a < b, то
если a < b и c - отрицательное число,
то ac > bc.
Следствие. Если a и b - положительные числа и a < b, то
Слайд 8
6. Если a < b и c < d, причем
a, b, c, d - положительные числа, то ac < bd.
Следствие. Если a и b - положительные числа и a < b, то где
Слайд 9 Решением неравенства с одной переменной называется значение переменной, которое
обращает его в верное числовое неравенство.
Решить неравенство - значит найти все его решения или доказать, что их нет.
Решить неравенство - значит найти все его решения или доказать, что их нет.
Слайд 10Неравенства, множества решений которых совпадают, называются равносильными.
Областью определения неравенства с одной
переменной называется множество значений переменной, при которых обе части неравенства имеют смысл.
Слайд 11Из данного неравенства получается равносильное ему неравенство, если:
1. из одной части
неравенства перенести в другую слагаемое с противоположным знаком;
Слайд 12Из данного неравенства получается равносильное ему неравенство, если:
2. обе части неравенства
умножить или разделить на одно и то же положительное число;
обе части неравенства умножить или разделить на одно и то же отрицательное число, изменив знак неравенства на противоположный;
обе части неравенства умножить или разделить на одно и то же отрицательное число, изменив знак неравенства на противоположный;
Слайд 13Из данного неравенства получается равносильное ему неравенство, если:
3. в какой -
либо части неравенства или в обеих его частях выполнить тождественное преобразование, не меняющее области определения неравенства.
Слайд 14Определение:
Показательными неравенствами называют неравенства вида a f(x) > a
g(x), где a > 0 и a ≠ 1, а также неравенства, сводящиеся к этому виду.
Слайд 15Теорема:
Показательное неравенство a f(x) > a g(x) равносильно неравенству того
же смысла f(x) > g(x), если a > 1;
показательное неравенство a f(x) > a g(x) равносильно неравенству противоположного смысла f(x) < g(x), если 0 < a < 1.
показательное неравенство a f(x) > a g(x) равносильно неравенству противоположного смысла f(x) < g(x), если 0 < a < 1.