- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Параллельные плоскости(11 класс)
Содержание
- 1. Презентация по математике на тему Параллельные плоскости(11 класс)
- 2. Если прямая, не лежащая в данной плоскости,
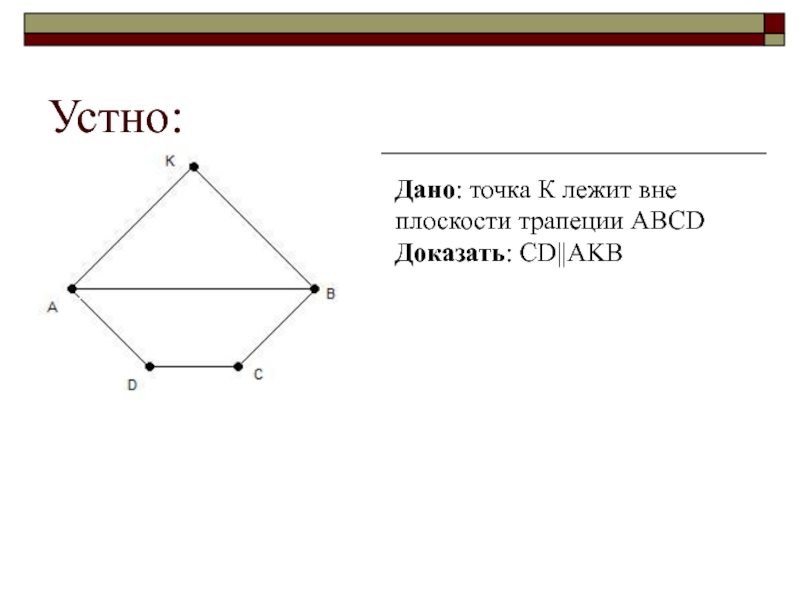
- 3. Устно:Дано: точка К лежит вне плоскости трапеции АВСDДоказать: СD||AKB
- 4. УТВЕРЖДЕНИЕ 1Если плоскость проходит через данную прямую,
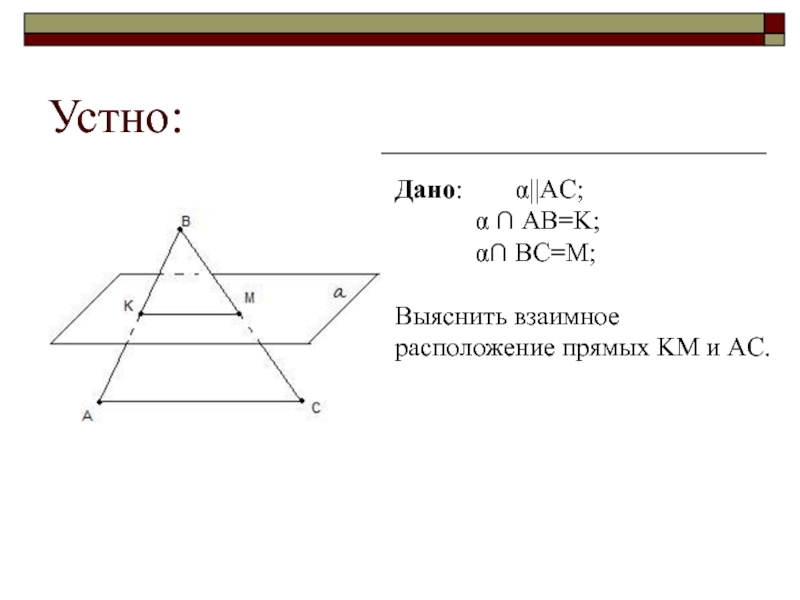
- 5. Устно:Дано: α||AC; α ∩ AB=K; α∩ BC=M;Выяснить взаимное расположение прямых KM и AC.
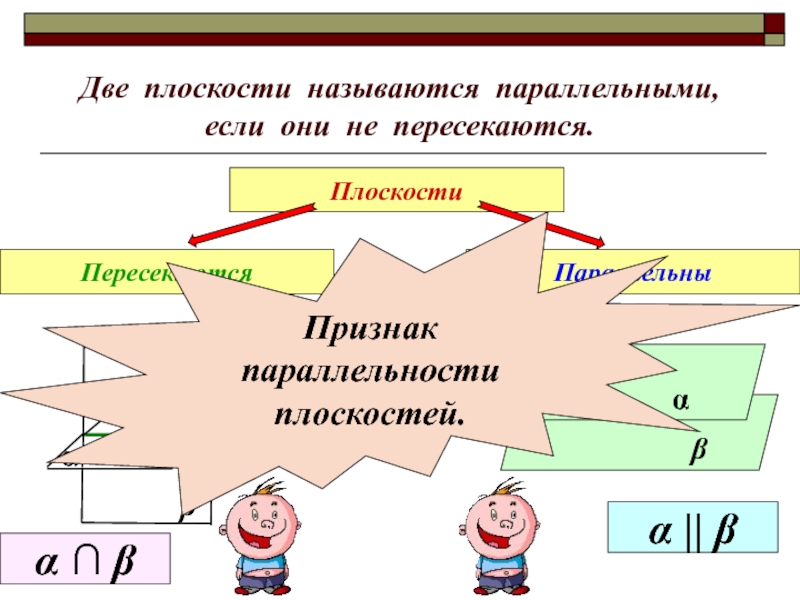
- 6. Две плоскости называются параллельными, если они не пересекаются.ПлоскостиПересекаютсяПараллельныβαα || β α ∩ β Признак параллельностиплоскостей.
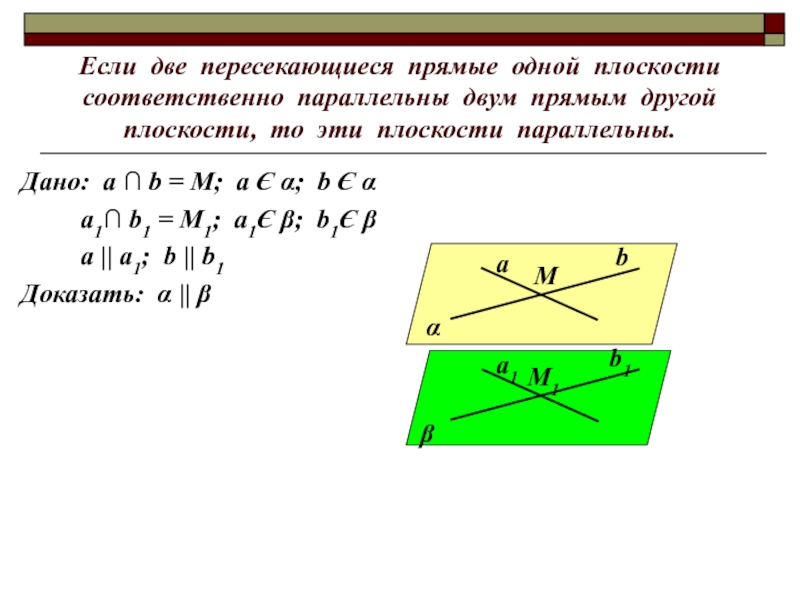
- 7. Если две пересекающиеся прямые одной плоскости соответственно
- 8. Если две пересекающиеся прямые одной плоскости соответственно
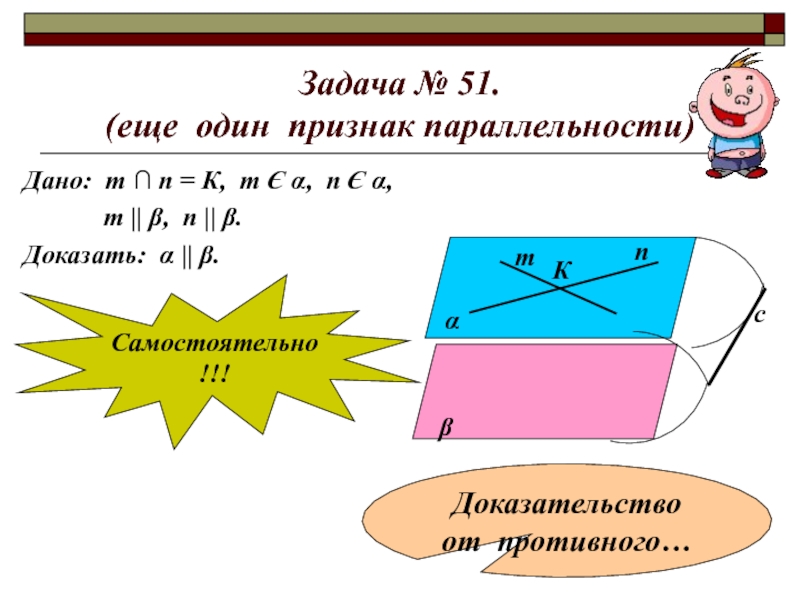
- 9. Задача № 51. (еще один признак параллельности)Дано:
- 10. Задача № 51. (еще один признак параллельности)Дано:
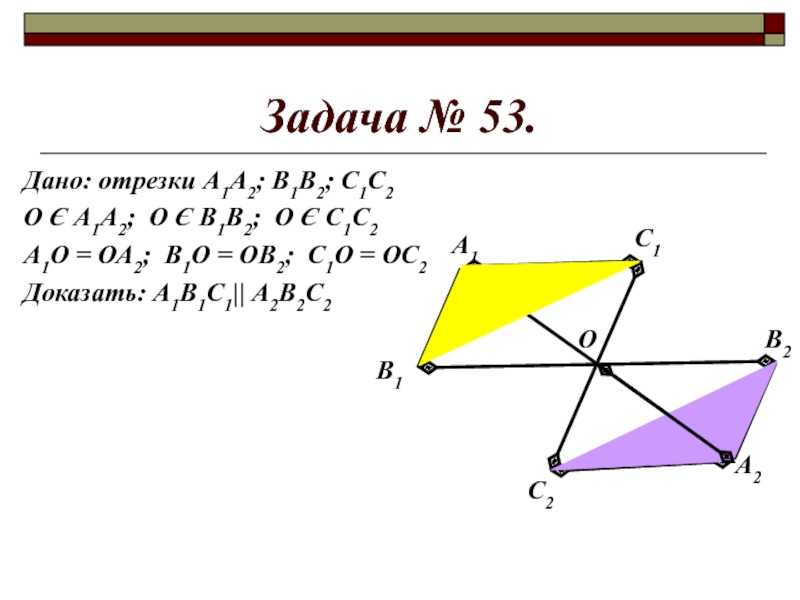
- 11. Задача № 53.Дано: отрезки А1А2; В1В2; С1С2О
- 12. Задача № 53.Дано: отрезки А1А2; В1В2; С1С2О
- 13. Задача № 54.МРNАВ DC
- 14. Задача № 54.МРNА DCВ
- 15. Ответьте на вопросы:Могут ли прямая и плоскость
- 16. Домашнее задание:П. 10, № 55; 56.
- 17. Дополнительное задание:Окружность радиуса 12 вписана в равнобедренную
Слайд 2Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей
ПРИЗНАК ПАРАЛЛЕЛЬНОСТИ ПРЯМОЙ И ПЛОСКОСТИ:
Слайд 4УТВЕРЖДЕНИЕ 1
Если плоскость проходит через данную прямую, параллельную другой плоскости, и
Слайд 6Две плоскости называются параллельными, если они не пересекаются.
Плоскости
Пересекаются
Параллельны
β
α
α || β
α
Признак
параллельности
плоскостей.
Слайд 7Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой
Дано: а ∩ b = М; а Є α; b Є α
а1∩ b1 = М1; а1Є β; b1Є β
a || a1; b || b1
Доказать: α || β
α
β
а
b
М
b1
а1
М1
Слайд 8Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой
Доказательство:
1) По признаку параллельности прямой и плоскости а || β, так как a||a1 и a1 € β.
Аналогично, b || β так как b||b1 и b1 € β.
Пусть α не параллельно β, т.е. α ∩ β = с
2) Т.к. а || β, а лежит в α; α ∩ β = с,
значит а || с.
3)Т.к. b || β, b лежит в α, α ∩ β = с,
значит b || с.
4) a||c, b||c, то есть а || b, следовательно
через точку М проходят
две прямые а и b,
параллельные прямой с.
Получили противоречие. Значит, α || β .
α
β
а
b
М
b1
а1
М1
с
Слайд 9Задача № 51.
(еще один признак параллельности)
Дано: т ∩ п = К,
т || β, п || β.
Доказать: α || β.
Самостоятельно!!!
Доказательство
от противного…
Слайд 10Задача № 51.
(еще один признак параллельности)
Дано: т ∩ п = К,
т || β, п || β.
Доказать: α || β.
1) Допустим, что ___________
2) Так как __________________,
то ______________________.
Получаем, что
______________________________________________________.
Вывод:
α ∩ β = с
п || β, т || β
т || с и п || с
через точку К проходят две прямые параллельные прямой с.
α || β
Слайд 11Задача № 53.
Дано: отрезки А1А2; В1В2; С1С2
О Є А1А2; О Є
А1О = ОА2; В1О = ОВ2; С1О = ОС2
Доказать: А1В1С1|| А2В2С2
А1
В1
А2
В2
С2
С1
О
Слайд 12Задача № 53.
Дано: отрезки А1А2; В1В2; С1С2
О Є А1А2; О Є
А1О = ОА2; В1О = ОВ2; С1О = ОС2
Доказать: А1В1С1 || А2В2С2
В2
С1
А1
В1
А2
С2
О
Слайд 15Ответьте на вопросы:
Могут ли прямая и плоскость не иметь общих точек?
Верно
Плоскости α и β параллельны, прямая т лежит в плоскости α. Верно ли, что прямая т параллельна плоскости β?
Верно ли, что если прямая а параллельна одной из двух параллельных плоскостей, с другой плоскостью прямая а имеет одну общую точку?
Верно ли, что плоскости параллельны, если прямая, лежащая в одной плоскости, параллельна другой плоскости?
Да
Нет
Да
Нет
Нет