- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Обучение решению текстовых задач
Содержание
- 1. Презентация по математике на тему Обучение решению текстовых задач
- 2. Текстовые задачи являются одним из сложных разделов
- 3. Цели: 1. Научить переводить реальные предметные ситуации
- 4. Этапы решения текстовых задачАнализ содержания задачи.Поиск пути
- 5. Задача «Движение навстречу друг другу» От пристани
- 6. Задача «Движение по воде» Рыболов отправляется в
- 7. «Задачи с известным объемом работы» Одна тракторная
Слайд 1Обучение решению текстовых задач в курсе алгебры 9 класса
(варианты ОГЭ)
Выполнила
Слайд 2
Текстовые задачи являются одним из сложных разделов в курсе обучения математике.
Текстовые задачи являются богатым материалом для ознакомления учащихся с новыми понятиями, для развития логического мышления, формирования межпредметных связей. Этапы решения задач формируют умение проводить исследования, развивают активность, наблюдательность, сообразительность, смекалку.
Представленные задачи взяты из сборников ОГЭ – 2016.
Слайд 3Цели:
1. Научить переводить реальные предметные ситуации в различные математические модели.
2.
Задачи:
1. Определение сложностей, которые испытывают учащиеся при решении текстовых задач и пути их решения.
2. Обобщение различных методов и приемов решения текстовых задач.
Слайд 4Этапы решения текстовых задач
Анализ содержания задачи.
Поиск пути решения и составление плана.
Краткая
Изображение условия задачи с помощью рисунка.
Алгоритм решения текстовых задач
Обозначить неизвестную величину через Х.
Выразить через нее другие величины.
Найти зависимость между величинами и составить уравнение
Решение уравнения.
Найти ответ на вопрос задачи, выполнить отбор решений по смыслу задачи.
Проверить правильность решения задачи. Записать ответ.
Слайд 5Задача «Движение навстречу друг другу»
От пристани А отошел теплоход
Через
со скоростью 45 км/ч.
45 км/ч
Через 45 минут
х(ч) – время до встречи первого теплохода;
162 км
A
В
(х-3/4)(ч) – время до встречи второго теплохода;
Итак, через
от пристани В навстречу ему отошел второй теплоход
со скоростью 36 км/ч.
если расстояние между пристанями А и В равно 162 км?
36 км/ч
Находим: (45х)(км) - расстояние до встречи первого теплохода;
(х -3/4 )▪ 36 (км) - расстояние до встречи второго теплохода.
По условию задачи расстояние между пристанями 162 км, составляем уравнение:
45х
(х - 3/4 )▪ 36
после отправления первого теплохода они встретились.
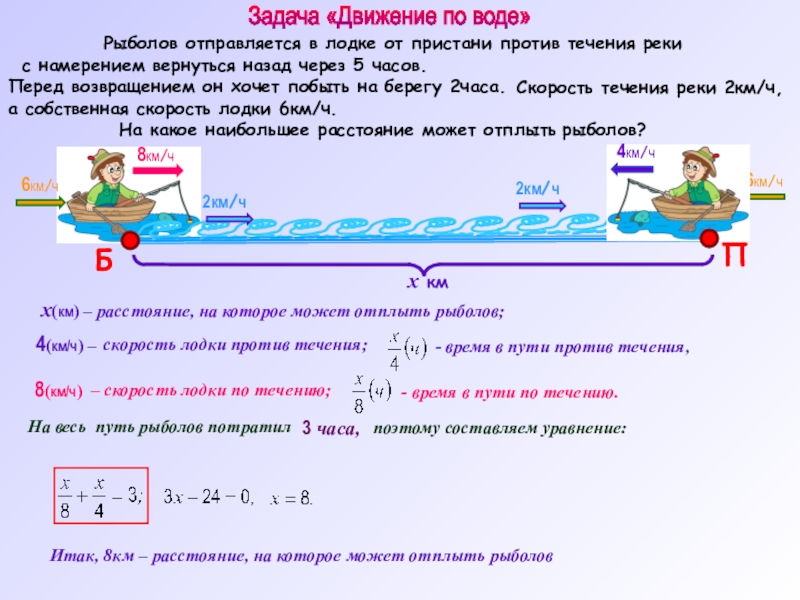
Слайд 6Задача «Движение по воде»
Рыболов отправляется в лодке от пристани против
х(км) – расстояние, на которое может отплыть рыболов;
х км
Б
П
с намерением вернуться назад через 5 часов.
Перед возвращением он хочет побыть на берегу 2часа.
- время в пути против течения,
На весь путь рыболов потратил
На какое наибольшее расстояние может отплыть рыболов?
поэтому составляем уравнение:
а собственная скорость лодки 6км/ч.
Скорость течения реки 2км/ч,
скорость лодки против течения;
– скорость лодки по течению;
- время в пути по течению.
Итак, 8км – расстояние, на которое может отплыть рыболов
3 часа,
4(км/ч) –
8(км/ч)
Слайд 7«Задачи с известным объемом работы»
Одна тракторная бригада должна была вспахать
х(га/день) –
Сколько гектаров вспахивала каждая бригада ежедневно?
Решение.
По условию задачи второй бригаде потребовалось на 2 дня больше, чем первой, т.е.
Решаем уравнение:
(дней) – потребуется первой бригаде для вспашки 240га;
Вспахивая ежедневно на 3га меньше второй бригады,
раньше, чем вторая бригада.
а другая - на 35% больше, чем первая.
первая все же закончила работу на 2 дня
(х+3)(га/день) –
(дней) – потребуется второй бригаде для вспашки 324га;
>
на 2
или
.
Итак, 24га или 15га в день вспахивала первая бригада,
производительность второй бригады;
производительность первой бригады;
тогда 27га или 18га в день вспахивала вторая.