приключение
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Наибольшее и наименьшее значение функции
Содержание
- 1. Презентация по математике на тему Наибольшее и наименьшее значение функции
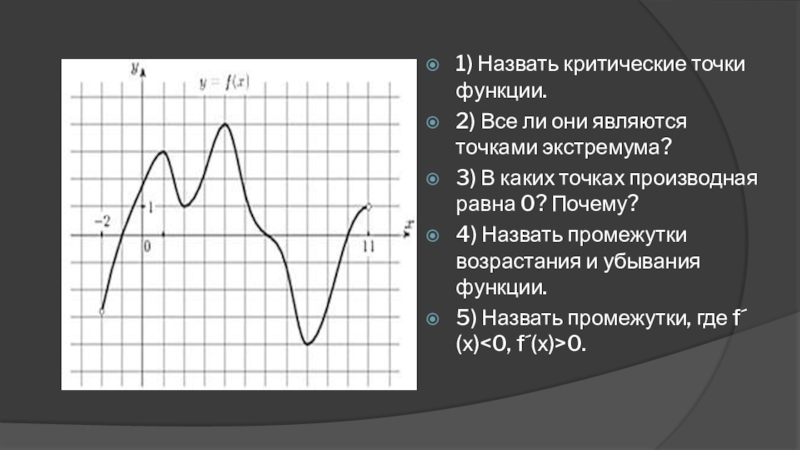
- 2. 1) Назвать критические точки функции.2) Все ли
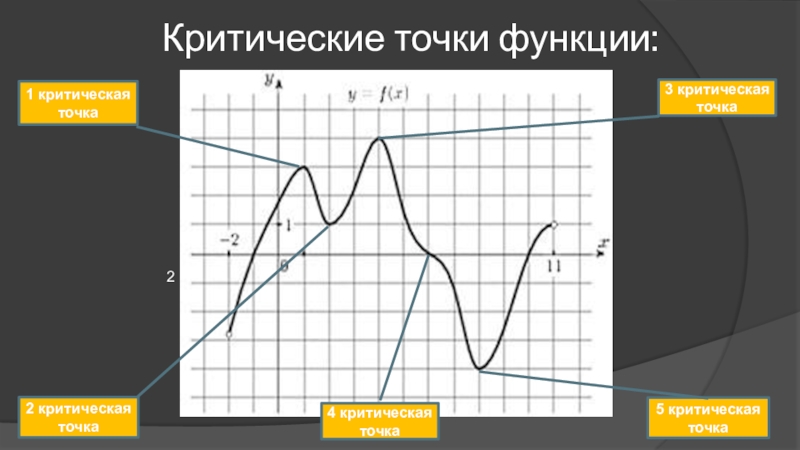
- 3. Критические точки функции:241 критическая точка2 критическая точка3 критическая точка4 критическая точка5 критическая точка
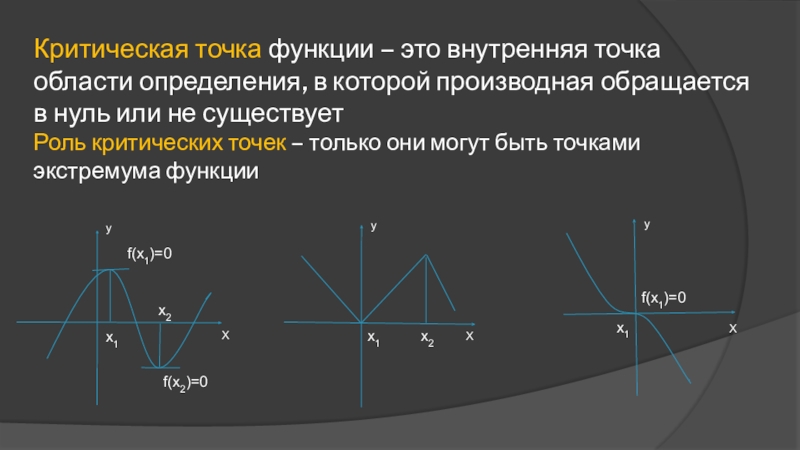
- 4. Критическая точка функции – это внутренняя точка
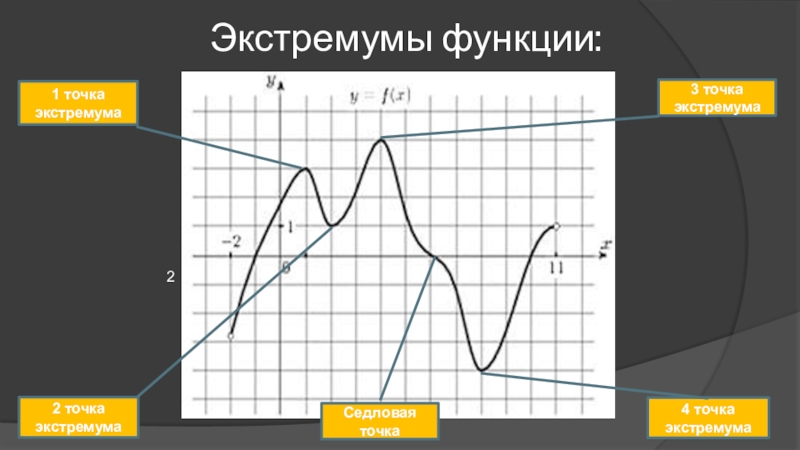
- 5. Экстремумы функции:241 точка экстремума2 точка экстремума3 точка экстремумаСедловая точка 4 точка экстремума
- 6. Точки из области определения функции, в которых
- 7. Производная равна 0 в точках:24В точке
- 8. В стационарной точке скорость изменения функции равна
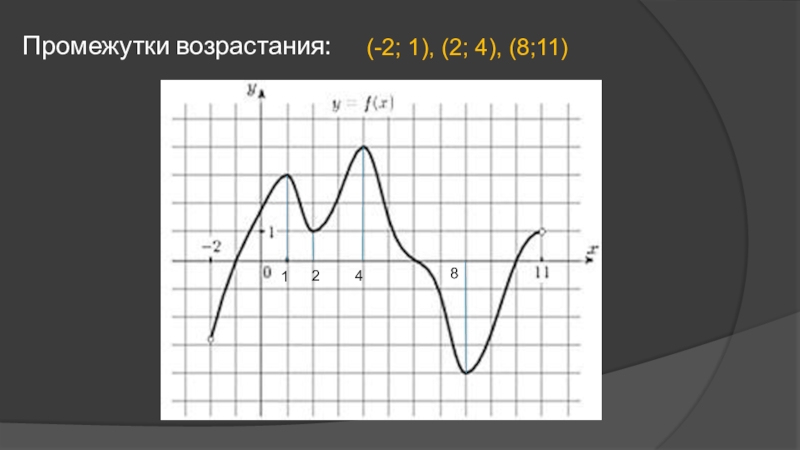
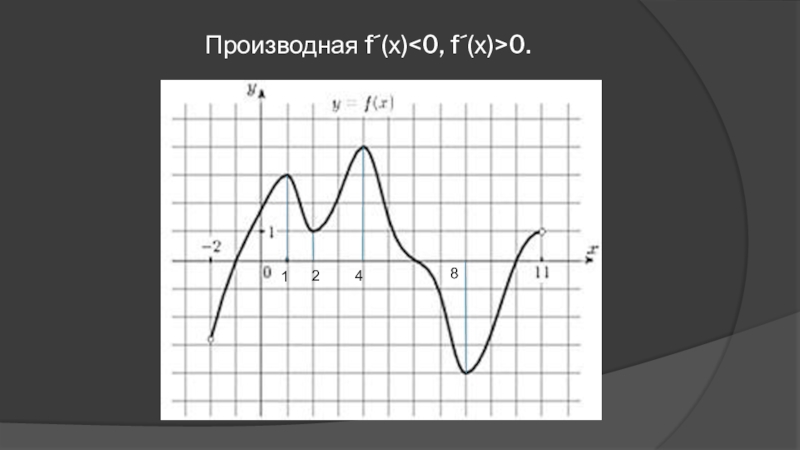
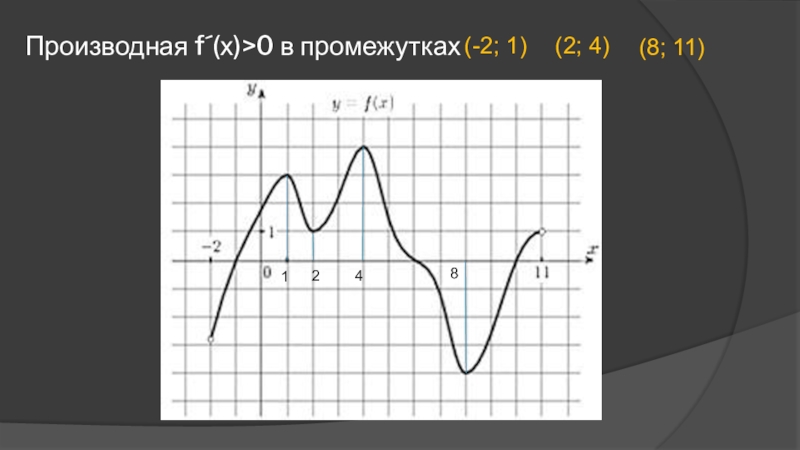
- 9. Промежутки возрастания:1248(-2; 1), (2; 4), (8;11)
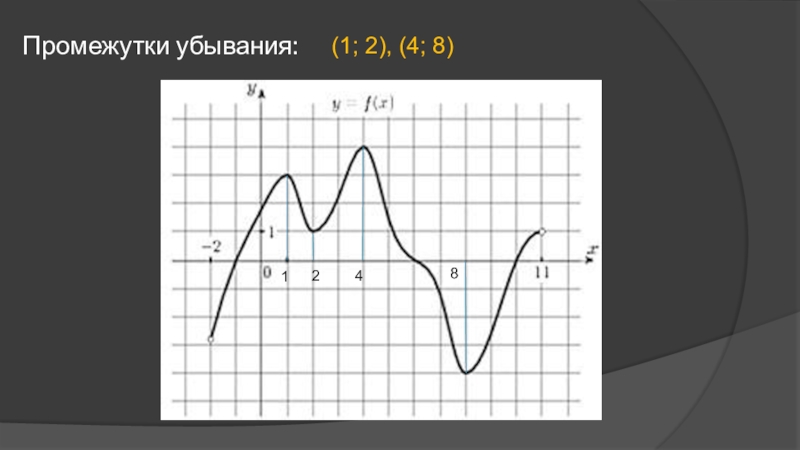
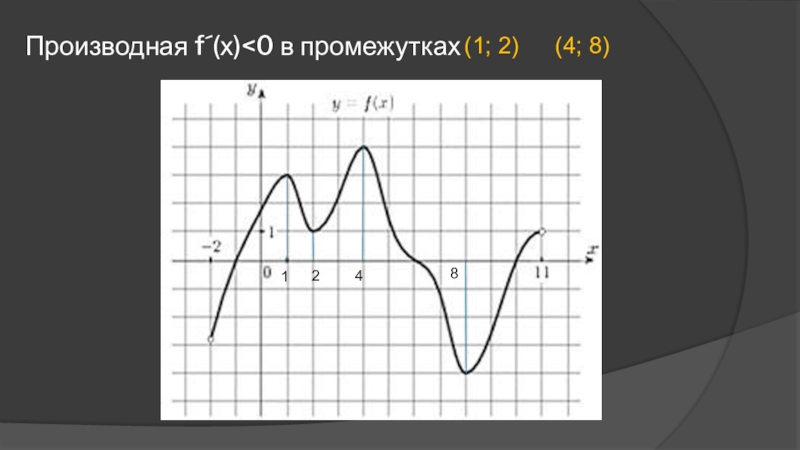
- 10. Промежутки убывания:1248(1; 2), (4; 8)
- 11. 1248Производная f´(х)0.
- 12. 1248Производная f´(х)>0 в промежутках (-2; 1)(2; 4)(8; 11)
- 13. Признак возрастания функции Если производная положительна f´(х)>0 на некотором промежутке, то функция возрастает на этом промежутке
- 14. 1248Производная f´(х)
- 15. Признак убывания функции Если производная отрицательна f´(х)
- 16. Слайд 16
- 17. Блиц – опрос Получи допуск к работе
- 18. Если функция f(x) дифференцируема на интервале (a;
- 19. Если функция у = f(х) непрерывна в
- 20. Если функция f(x) дифференцируема на интервале (a;
- 21. Точки, в которых производная функции равна 0, называются ______________стационарными
- 22. Слайд 22
- 23. Наибольшее и наименьшее значение функцииЦель:Научиться находить наибольшее
- 24. Слайд 24
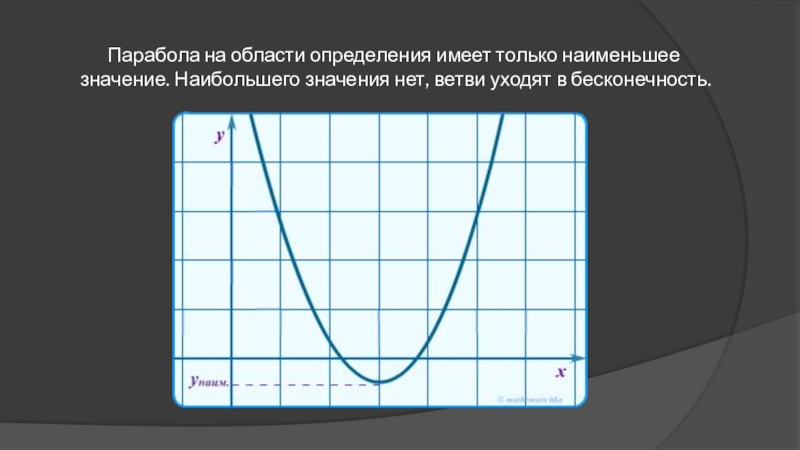
- 25. Парабола на области определения имеет только наименьшее значение. Наибольшего значения нет, ветви уходят в бесконечность.
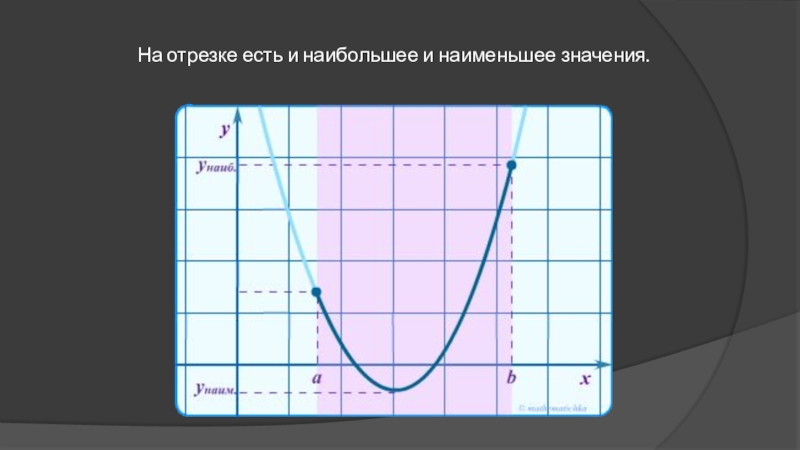
- 26. На отрезке есть и наибольшее и наименьшее значения.
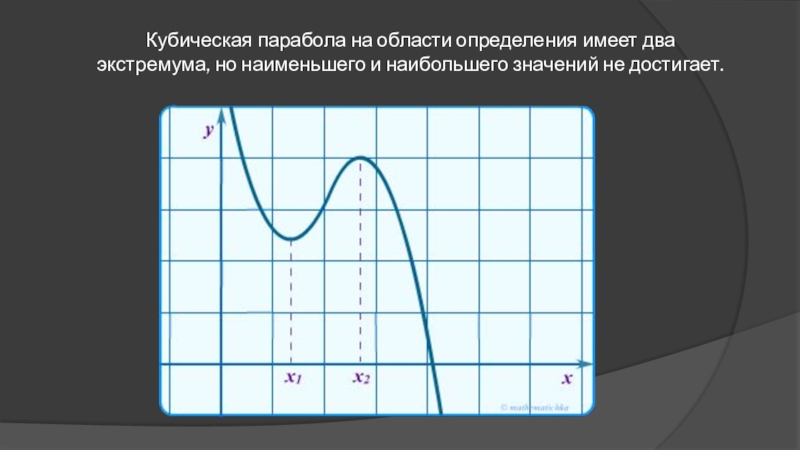
- 27. Кубическая парабола на области определения имеет два экстремума, но наименьшего и наибольшего значений не достигает.
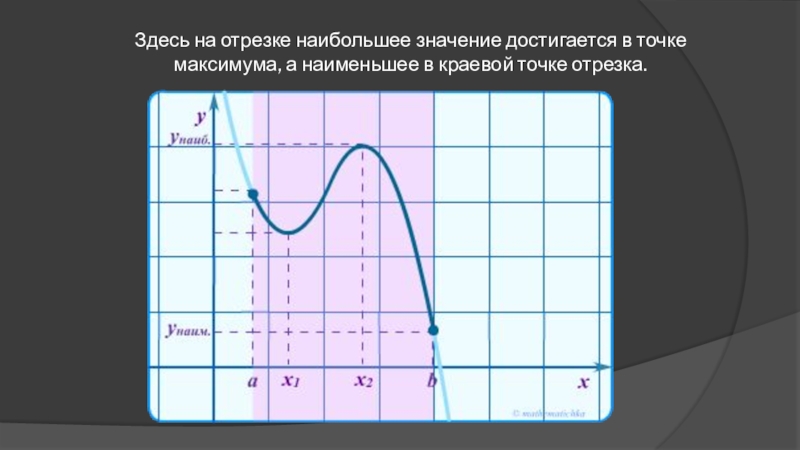
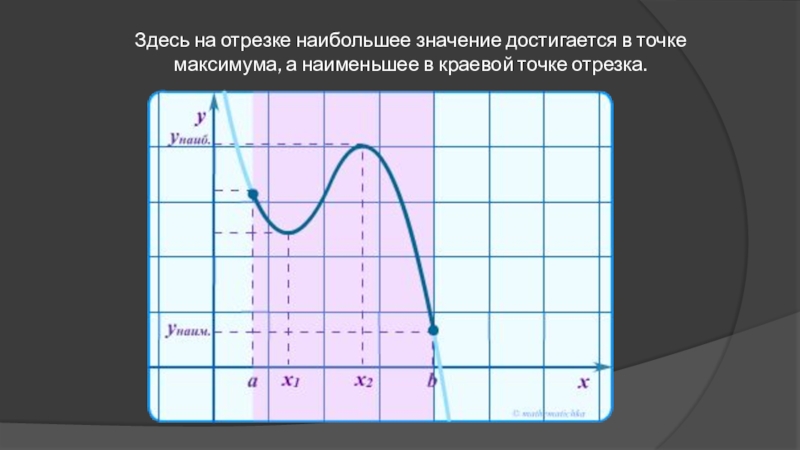
- 28. Здесь на отрезке наибольшее значение достигается в точке максимума, а наименьшее в краевой точке отрезка.
- 29. Здесь на отрезке наибольшее значение достигается в точке максимума, а наименьшее в краевой точке отрезка.
- 30. Функция может достигать своих наибольших и наименьших
- 31. Работаем по учебнику самостоятельно!Упражнение 281, стр. 119
- 32. Слайд 32
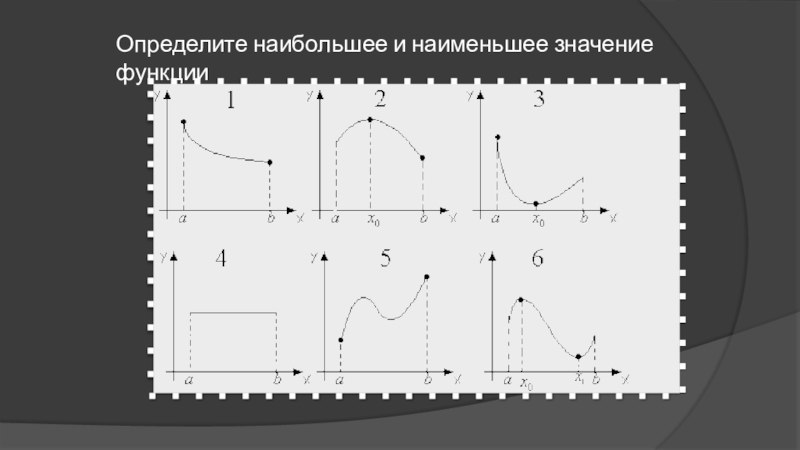
- 33. Определите наибольшее и наименьшее значение функции
- 34. Функция достигает своего наибольшего значения на левой
- 35. Функция постоянна на промежутке, т.е. она достигает
- 36. Давайте обобщим, в каких точках на
- 37. Слайд 37
- 38. Слайд 38
- 39. Самостоятельная работа П л а н
- 40. Слайд 40
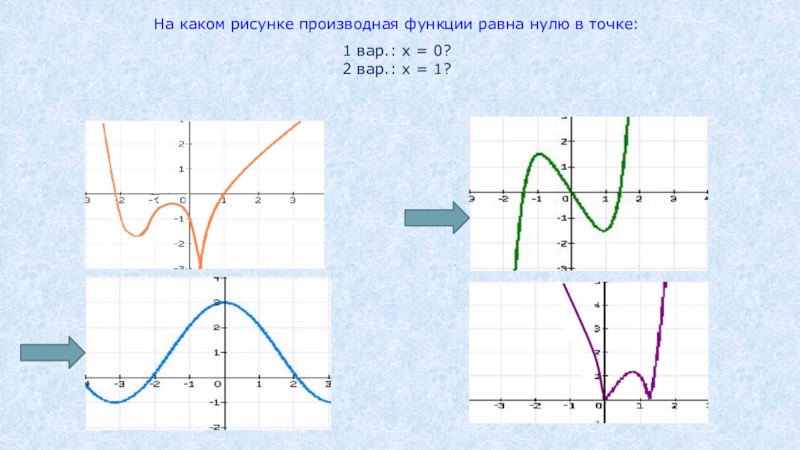
- 41. На каком рисунке производная функции равна нулю
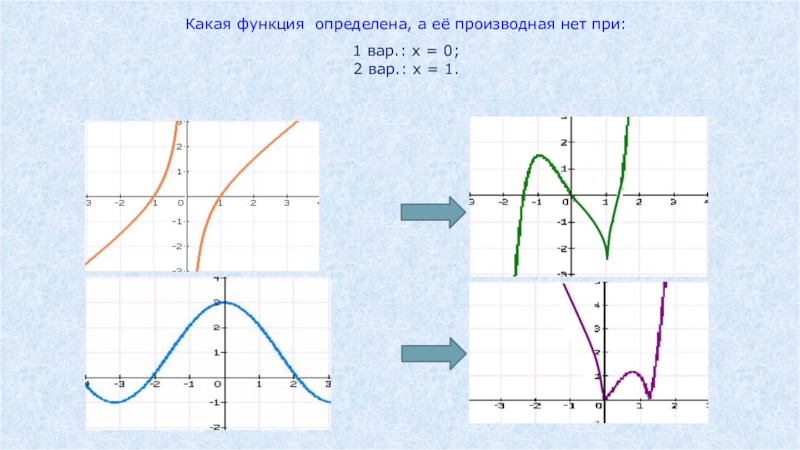
- 42. Какая функция определена, а её производная нет при:1 вар.: х = 0;2 вар.: х = 1.
- 43. На каком рисунке график функции имеет ровно
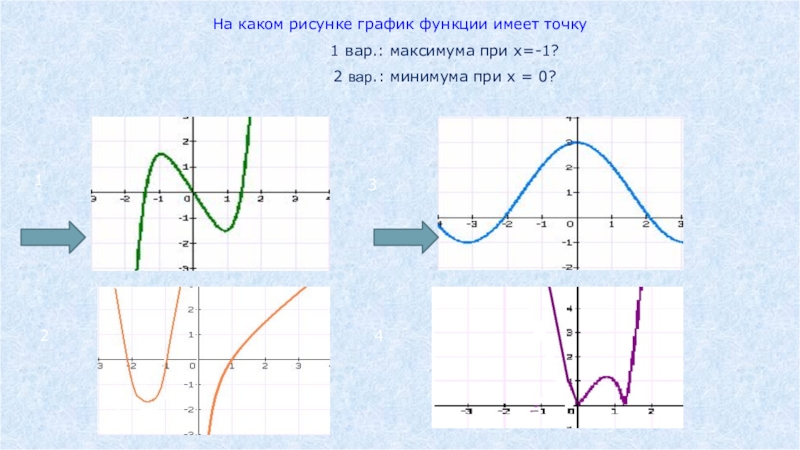
- 44. На каком рисунке график функции имеет точку
- 45. Для какой функции на интервале 1вар.:
- 46. Слайд 46
- 47. 1. Если функция непрерывна на отрезке, то
- 48. Слайд 48
- 49. Задача. Самый тяжелый брус. Из цилиндрического бревна
- 50. Ребята, заполните пожалуйста лист самооценки и передайте мне!
- 51. БЛАГОДАРЮ ЗА УЧАСТИЕ И ВНИМАНИЕ!УСПЕХОВ В УЧЕБЕИ БУДЬТЕ ЗДОРОВЫ!!!
- 52. Слайд 52
1) Назвать критические точки функции.2) Все ли они являются точками экстремума?3) В каких точках производная равна 0? Почему?4) Назвать промежутки возрастания и убывания функции.5) Назвать промежутки, где f´(х)0.
Слайд 21) Назвать критические точки функции.
2) Все ли они являются точками экстремума?
3)
В каких точках производная равна 0? Почему?
4) Назвать промежутки возрастания и убывания функции.
5) Назвать промежутки, где f´(х)<0, f´(х)>0.
4) Назвать промежутки возрастания и убывания функции.
5) Назвать промежутки, где f´(х)<0, f´(х)>0.
Слайд 3 Критические точки функции:
2
4
1 критическая точка
2 критическая точка
3 критическая точка
4 критическая
точка
5 критическая точка
Слайд 4Критическая точка функции – это внутренняя точка области определения, в которой
производная обращается в нуль или не существует
Роль критических точек – только они могут быть точками экстремума функции
Роль критических точек – только они могут быть точками экстремума функции
х2
х1
у
Х
Х
у
х2
х1
у
Х
х1
f(x1)=0
f(x2)=0
f(x1)=0
Слайд 5Экстремумы функции:
2
4
1 точка экстремума
2 точка экстремума
3 точка экстремума
Седловая точка
4 точка
экстремума
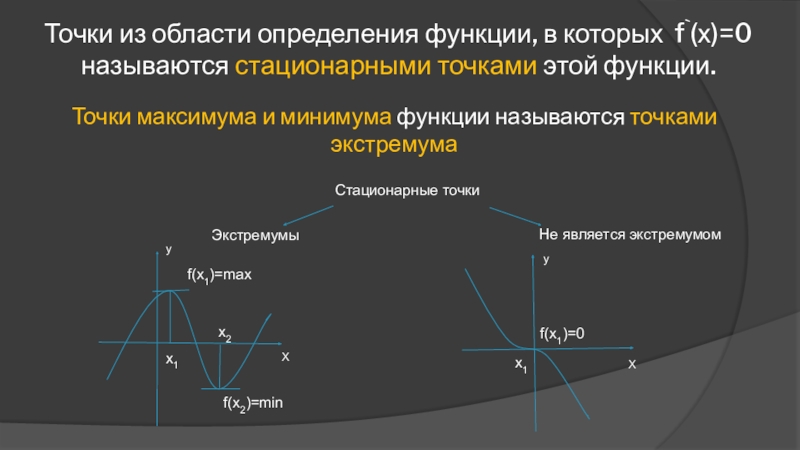
Слайд 6Точки из области определения функции, в которых f`(х)=0 называются стационарными точками
этой функции.
Экстремумы
Не является экстремумом
Стационарные точки
Точки максимума и минимума функции называются точками экстремума
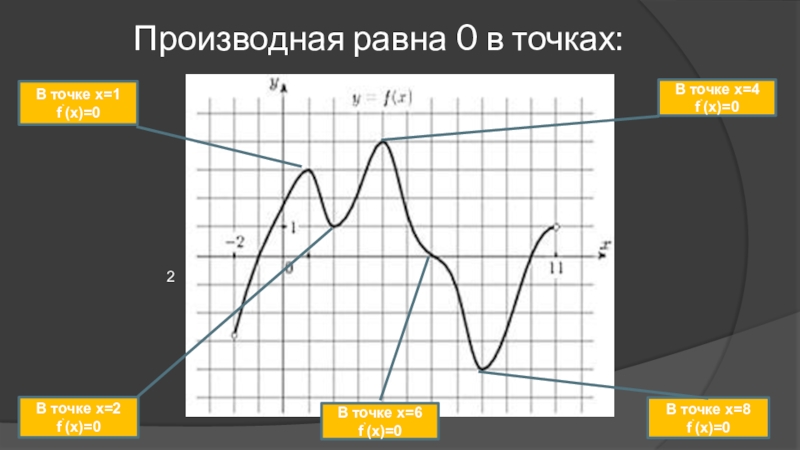
Слайд 7 Производная равна 0 в точках:
2
4
В точке х=1 f`(x)=0
В точке х=2
f`(x)=0
В точке х=4 f`(x)=0
В точке х=6 f`(x)=0
В точке х=8 f`(x)=0
Слайд 8В стационарной точке скорость изменения функции равна нулю, то есть функция
«на мгновение» перестает меняться
Касательная в стационарных точках горизонтальна, то есть образует нулевой угол с осью Х.
Поэтому f` (x)=0
Слайд 13Признак возрастания функции
Если производная положительна f´(х)>0 на некотором промежутке, то
функция возрастает на этом промежутке
Слайд 15Признак убывания функции
Если производная отрицательна f´(х)
функция убывает на этом промежутке
Слайд 18Если функция f(x) дифференцируема на интервале (a; b) и
f '
(х) > 0 для всех х Є (a; b) , то функция __________ на
интервале (a; b)
интервале (a; b)
Если функция f(x) дифференцируема на интервале (a; b) и
f '(х) __ 0 для всех х Є (a; b) , то функция возрастает на интервале (a; b)
Пусть функция f(x) дифференцируема на интервале (a; b) , х0 Є (a; b) , и f '(х0 ) = 0. Тогда если при переходе через стационарную точку х0 функции f(х) ее производная меняет знак с “+” на “–”, то точка х0 – точка _________ функции f(x)
возрастает
>
максимума
Слайд 19Если функция у = f(х) непрерывна в точке х0 и производная
в этой точке меняет знак с “___” на “___”, то х0 - точка минимума
Если х0 - точка экстремума функции у = f(х), то производная в этой точке равна ___.
Если функция f(x) дифференцируема на интервале (a; b) и
f '(х) ___0 для всех х Є (a; b) , то функция убывает на интервале (a; b)
-
0
<
+
Слайд 20Если функция f(x) дифференцируема на интервале (a; b) и
f '(х)
< 0 для всех х Є (a; b) , то функция ___________ на
интервале (a; b)
интервале (a; b)
Пусть функция f(x) дифференцируема на интервале (a; b) ,
х0 Є (a; b) , и f '(х0) = 0. Тогда если при переходе через стационарную точку х0 функции f(х) ее производная меняет знак с “–” на “+”, то точка х0 – точка ____________ функции f(x)
Если функция у = f(х) непрерывна в точке х0 и производная в этой точке меняет знак с “___” на “___”, то х0 - точка максимума.
минимума
+
убывает
-
Слайд 23Наибольшее и наименьшее значение функции
Цель:
Научиться находить наибольшее и наименьшее
значение функции
2.
Составить алгоритм нахождения
наибольшего и наименьшего значения функции
наибольшего и наименьшего значения функции
Тема:
Слайд 25Парабола на области определения имеет только наименьшее значение. Наибольшего значения нет,
ветви уходят в бесконечность.
Слайд 27Кубическая парабола на области определения имеет два экстремума, но наименьшего и
наибольшего значений не достигает.
Слайд 28Здесь на отрезке наибольшее значение достигается в точке максимума, а наименьшее
в краевой точке отрезка.
Слайд 29Здесь на отрезке наибольшее значение достигается в точке максимума, а наименьшее
в краевой точке отрезка.
Слайд 30Функция может достигать своих
наибольших и наименьших значений
либо на внутренних
точках промежутка,
либо на его границах.
либо на его границах.
Вывод:
Слайд 34Функция достигает своего наибольшего значения на левой границе промежутка в точке
х = а , а своего наименьшего значения на правой границе промежутка в точке х = в
Функция достигает своего наибольшего значения в точке х = х0 (это точка максимума) , а своего наименьшего значения на правой границе промежутка в точке х = в .
Функция достигает своего наибольшего значения на левой границе промежутка в точке х = а , а своего наименьшего значения в точке х = х0 (это точка минимума).
Слайд 35Функция постоянна на промежутке, т.е. она достигает своего минимального и максимального
значения в любой точке промежутка, причем минимальное и максимальное значения равны между собой.
Функция достигает своего наибольшего значения в точке х = в , а своего наименьшего значения точке х = а (несмотря на то, что функция имеет на этом промежутке как максимум, так и минимум).
Функция достигает своего наибольшего значения в точке х = х0 (это точка максимума), а своего наименьшего значения в точке х = х1 (это точка минимума).
Слайд 36 Давайте обобщим, в каких точках на отрезке функция может принимать
наибольшее или наименьшее значение?
Функция может принимать наибольшее и наименьшее значение в критических точках или на концах отрезка.
Слайд 39Самостоятельная работа
П л а н р е ш
е н и я:
1) Найдите производную функции .
2) Найдите критические точки функции.
3) Вычислите значения функции на концах отрезка и в критических точках.
4) Среди найденных значений функций выберите наибольшее и наименьшее.
5) Запишите ответ
1) Найдите производную функции .
2) Найдите критические точки функции.
3) Вычислите значения функции на концах отрезка и в критических точках.
4) Среди найденных значений функций выберите наибольшее и наименьшее.
5) Запишите ответ
Вариант 2. Найдите наибольшее и наименьшее значения функции
f(x) = 1-4x+x2 на отрезке [0;4].
Вариант 1. Найдите наибольшее и наименьшее значение функции
f(x) = x3 /3-x2 +1 на отрезке [-1;1].
Слайд 43На каком рисунке график функции имеет ровно две критические точки на
интервале
1 вар.: [-2;2]?
2 вар.: [-2;0]?
1 вар.: [-2;2]?
2 вар.: [-2;0]?
![На каком рисунке график функции имеет ровно две критические точки на интервале 1 вар.: [-2;2]?2 вар.: [-2;0]?](/img/thumbs/b004dc2119205f72768aebd37dd170a9-800x.jpg "Презентация по математике на тему Наибольшее и наименьшее значение функции На каком рисунке график функции имеет ровно две критические точки на")
Слайд 44На каком рисунке график функции имеет точку
1 вар.: максимума при х=-1?
2 вар.: минимума при х = 0?
2 вар.: минимума при х = 0?
1
2
3
4
Слайд 45Для какой функции на интервале 1вар.: [1; 2] производная отрицательна? 2
вар.: [-1; 0] производная отрицательна?
1
2
3
4
![Для какой функции на интервале 1вар.: [1; 2] производная отрицательна? 2 вар.: [-1; 0] производная](/img/thumbs/cc427f8f583b24f156325112e729d844-800x.jpg "Презентация по математике на тему Наибольшее и наименьшее значение функции Для какой функции на интервале 1вар.: [1; 2] производная отрицательна? 2 вар.: [-1; 0] производная отрицательна?1234")
Слайд 471. Если функция непрерывна на отрезке, то она достигает на нем
и своего наибольшего, и своего наименьшего значений.
2. Наибольшего и наименьшего значений непрерывная функция может достигать как на концах отрезка, так и внутри него.
3. Если наибольшее (или наименьшее) значение достигается внутри отрезка, то только в стационарной или критической точке.
2. Наибольшего и наименьшего значений непрерывная функция может достигать как на концах отрезка, так и внутри него.
3. Если наибольшее (или наименьшее) значение достигается внутри отрезка, то только в стационарной или критической точке.
ВЕРНО ЛИ УТВЕРЖДЕНИЕ?
Слайд 49Задача. Самый тяжелый брус.
Из цилиндрического бревна нужно выпилить брус наибольшего
веса. Как это сделать?
§3, стр 115 – 119, упражнение № 282
ДОМАШНЕЕ ЗАДАНИЕ
