математики ,г.Шарыпово
Средняя школа №2
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Медиана,биссектриса, высота (7 класс)
Содержание
- 1. Презентация по математике на тему Медиана,биссектриса, высота (7 класс)
- 2. Цели урока:Проверить знание о треугольникеПознакомиться: с медианой, биссектрисой, высотой треугольника. Равнобедренный треугольник и его свойства.
- 3. ПовторениеСамостоятельная работа: 1. Виды треугольников: по сторонам; по углам.( сделать чертежики)2. Написать о равнобедренном треугольники
- 4. Медианы треугольникаМедиа́на треуго́льника (лат. mediāna — средняя) ― отрезок внутри треугольника,
- 5. А В А Отрезок биссектрисы угла треугольника,
- 6. Высоты треугольникаВысота треугольника — перпендикуляр, проведённый из вершины треугольника к прямой, содержащей
- 7. СВОЙСТВА РАВНОБЕДРЕННОГО ТРЕУГОЛЬНИКА
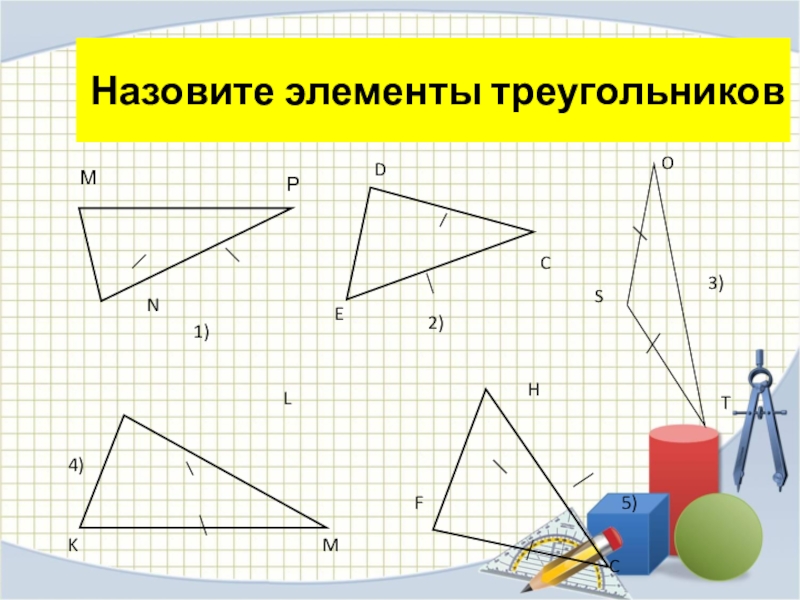
- 8. Назовите элементы треугольников
- 9. Теорема 1В равнобедренном треугольнике углыпри основании равныДано:
- 10. Доказательство:Проведём ВD – биссектрису ΔАВС2. Рассмотрим ΔАВD
- 11. 1ВОтветАСНаводящие вопросы (4) Суммой каких углов являетсяугол
- 12. Как называется отрезок АМ на рисунке?Сформулировать определение
- 13. Как называется отрезок ВК на рисунке?Сформулировать определение
- 14. Как называется отрезок СН на рисунке?Сформулировать определение
Цели урока:Проверить знание о треугольникеПознакомиться: с медианой, биссектрисой, высотой треугольника. Равнобедренный треугольник и его свойства.
Слайд 1Медианы, биссектрисы и высоты треугольника.
Свойства равнобедренного треугольника
Выполнила: Л. В. Демиденко- учитель
Слайд 2Цели урока:
Проверить знание о треугольнике
Познакомиться: с медианой, биссектрисой, высотой треугольника. Равнобедренный
треугольник и его свойства.
Слайд 3Повторение
Самостоятельная работа:
1. Виды треугольников: по сторонам; по углам.( сделать чертежики)
2.
Написать о равнобедренном треугольники
Слайд 4
Медианы треугольника
Медиа́на треуго́льника (лат. mediāna — средняя) ― отрезок внутри треугольника, соединяющий вершину треугольника с
серединой противоположной стороны
На рисунке АА₁ , ВВ₁ и СС₁ – медианы.
Свойства медиан
1. Медианы треугольника точкой их пересечения делятся в отношении 2:1 (считая от вершин треугольника).
2. Медиана делит треугольник на два равновеликих треугольника. (Два треугольника равновелики, если их площади равны.)
3. Три медианы треугольника делят треугольник на шесть равновеликих треугольников
Слайд 5А
В
А
Отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с
точкой противоположной стороны, называется биссектрисой треугольника.
С
1
Биссектриса треугольника
АА1 – биссектриса треугольника
Слайд 6
Высоты треугольника
Высота треугольника — перпендикуляр, проведённый из вершины треугольника к прямой, содержащей противоположную сторону.
В остроугольном треугольнике
все три высоты лежат внутри треугольника.
В тупоугольном треугольнике две высоты пересекают продолжение сторон и лежат вне треугольника; третья высота пересекает сторону треугольника.
В тупоугольном треугольнике две высоты пересекают продолжение сторон и лежат вне треугольника; третья высота пересекает сторону треугольника.
Слайд 9Теорема 1
В равнобедренном треугольнике углы
при основании равны
Дано: ΔАВС – равнобедренный,
АС – основание
Доказать: ∠А =∠С
Доказать: ∠А =∠С
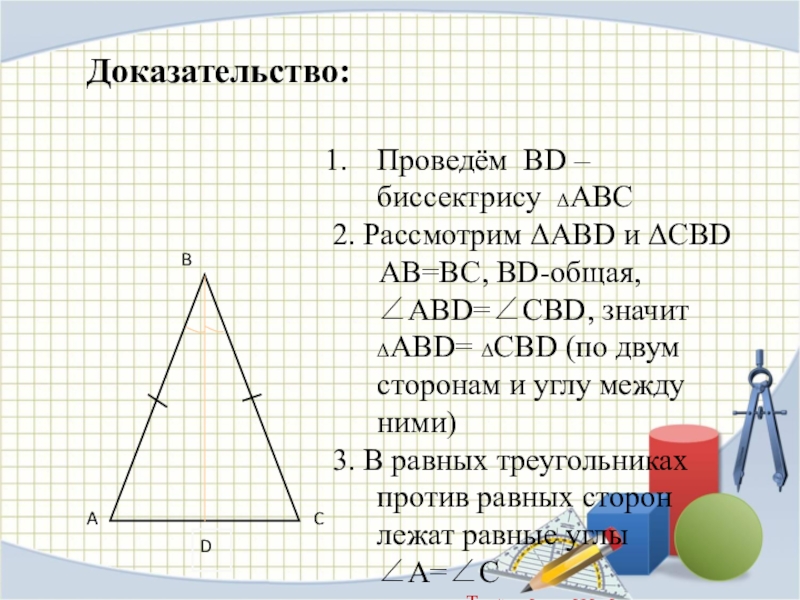
Слайд 10Доказательство:
Проведём ВD – биссектрису ΔАВС
2. Рассмотрим ΔАВD и ΔСВD
АВ=ВС, ВD-общая, ∠АВD=∠СВD, значит ΔАВD= ΔСВD (по двум сторонам и углу между ними)
3. В равных треугольниках против равных сторон лежат равные углы ∠А=∠С
Теорема доказана
3. В равных треугольниках против равных сторон лежат равные углы ∠А=∠С
Теорема доказана
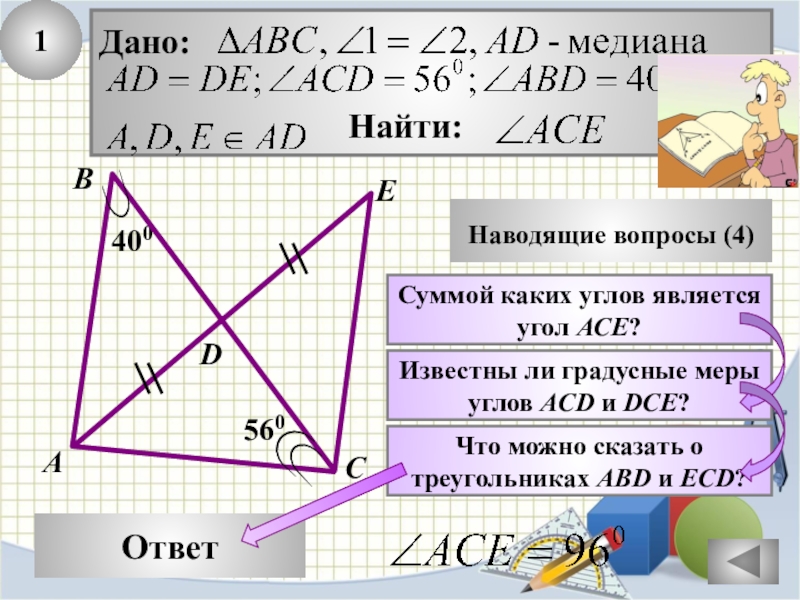
Слайд 111
В
Ответ
А
С
Наводящие вопросы (4)
Суммой каких углов является
угол АСЕ?
D
560
400
E
Известны ли градусные
меры
углов АСD и DCE?
углов АСD и DCE?
Что можно сказать о
треугольниках АBD и ECD?
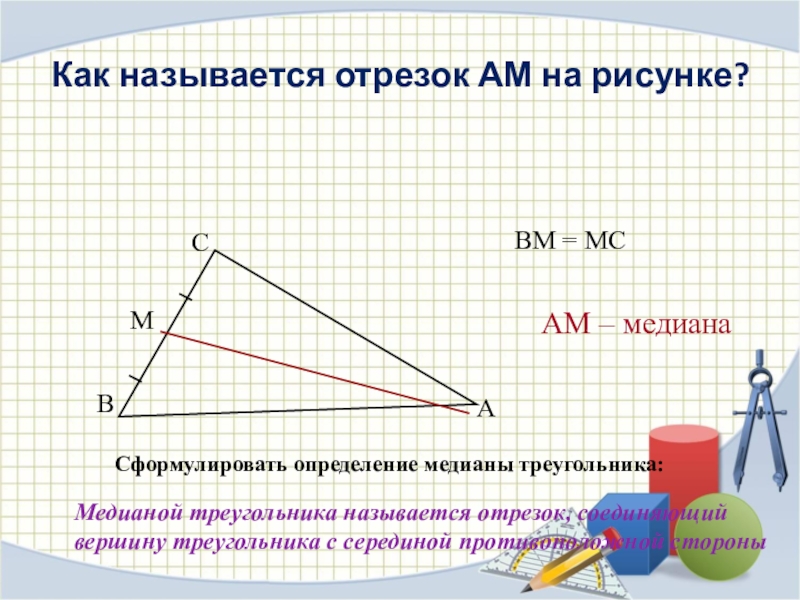
Слайд 12Как называется отрезок АМ на рисунке?
Сформулировать определение медианы треугольника:
Медианой треугольника называется
отрезок, соединяющий вершину треугольника с серединой противоположной стороны
АМ – медиана
ВМ = МС
Слайд 13Как называется отрезок ВК на рисунке?
Сформулировать определение биссектрисы треугольника:
Биссектрисой треугольника называется
отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны.
ВК - биссектриса
∠АВК = ∠СВК
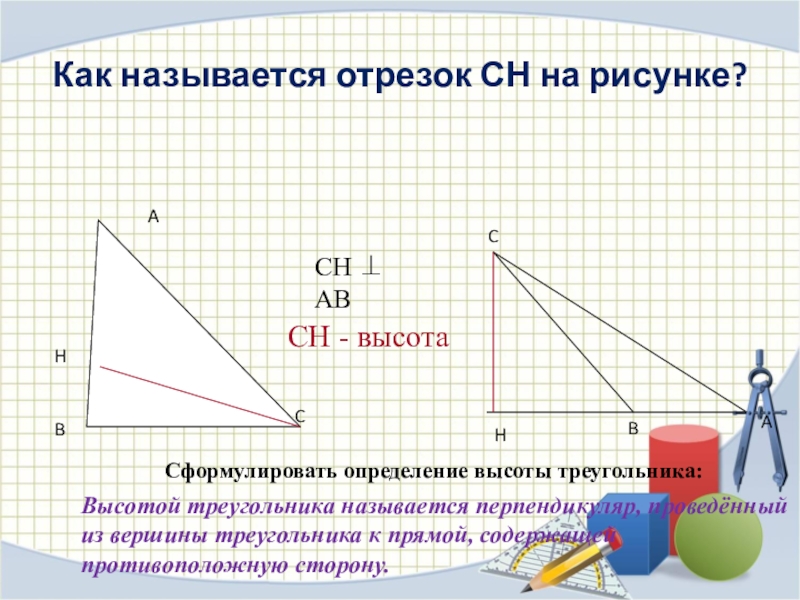
Слайд 14Как называется отрезок СН на рисунке?
Сформулировать определение высоты треугольника:
Высотой треугольника называется
перпендикуляр, проведённый из вершины треугольника к прямой, содержащей противоположную сторону.
СН - высота
СН ⊥ АВ
