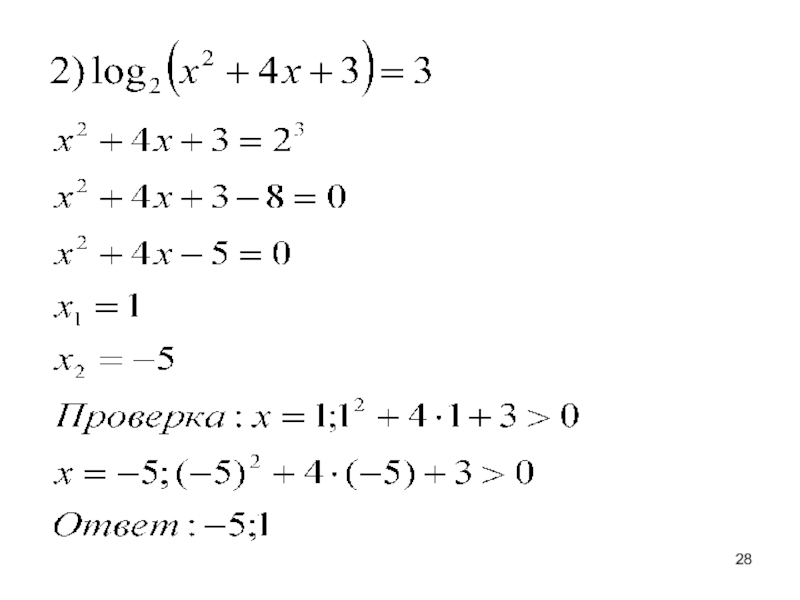- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Логарифмическая функция, логарифмы, уравнения, неравенства
Содержание
- 1. Презентация по математике на тему Логарифмическая функция, логарифмы, уравнения, неравенства
- 2. Из истории логарифмов Немного об изобретателе
- 3. К идее логарифмических
- 4. Определение логарифма: Логарифмом числа b по основанию
- 5. пример1.
- 6. Логарифм с основанием 10 называется десятичным логарифмом и обозначается
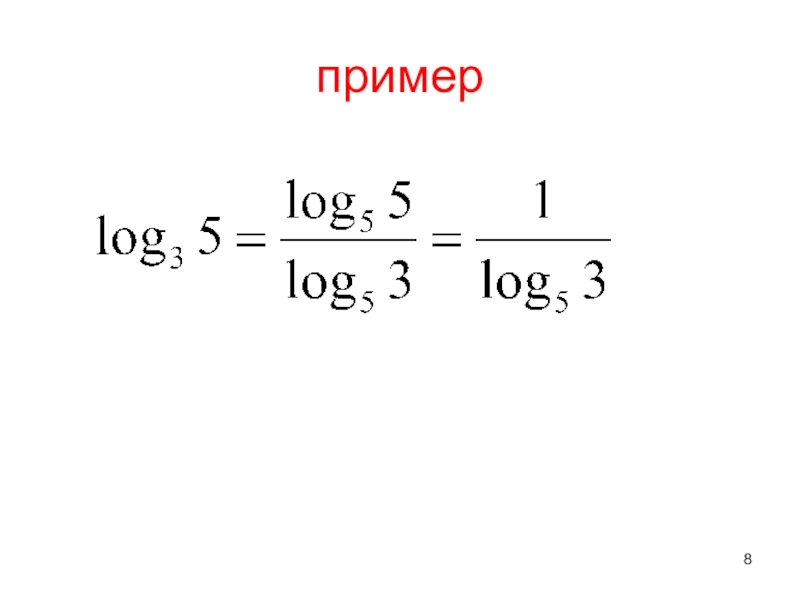
- 7. Формула перехода от одного основания логарифма к
- 8. пример
- 9. Основное логарифмическое тождество:
- 10. Примеры
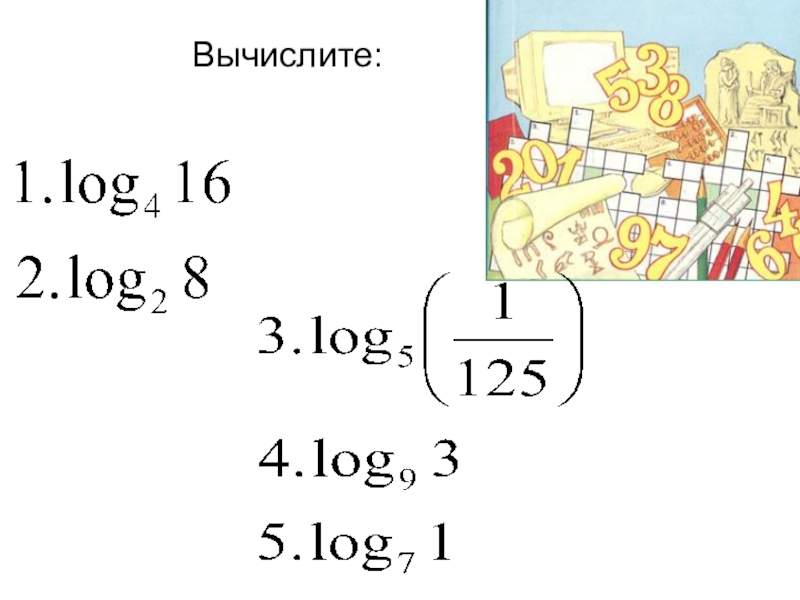
- 11. Вычислите:
- 12. Ответы23-31/20
- 13. Свойства логарифмовПри любых а>0, а ≠ 1
- 14. Примеры1.2.3.4.
- 15. Логарифмическая функция
- 16. Определение: Функцию, заданную формулойу = logaf(x) называют
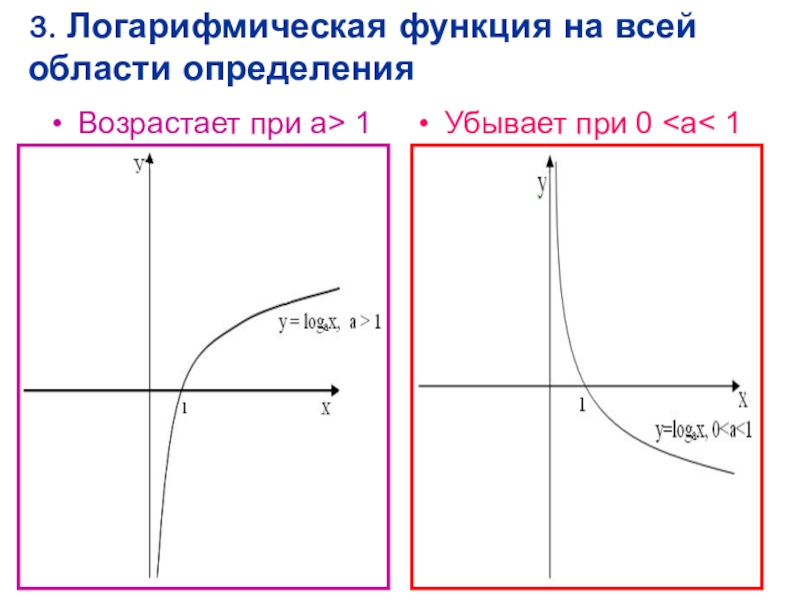
- 17. Возрастает при а> 1Убывает при 0
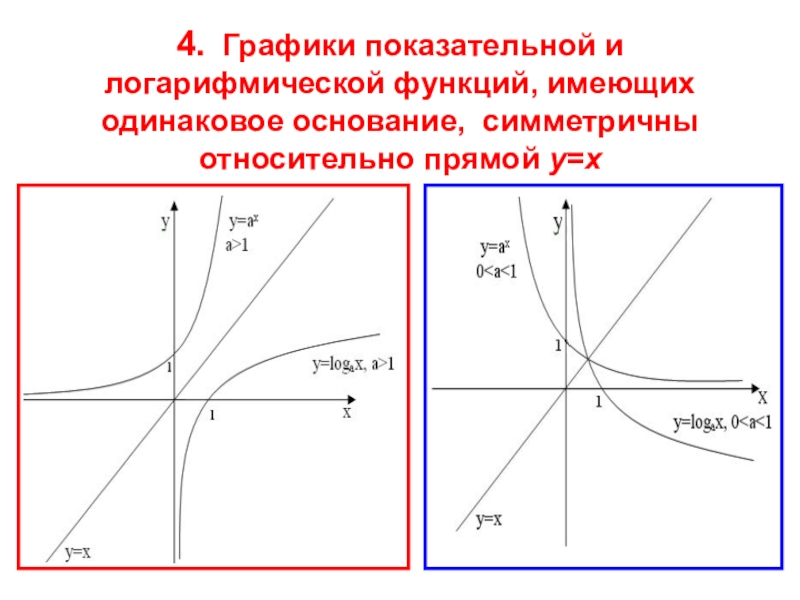
- 18. 4. Графики показательной и логарифмической функций, имеющих одинаковое основание, симметричны относительно прямой у=х
- 19. ПримерыНайти область определения функции:1.Область определения логарифмической функции-
- 20. 2. Корни данного квадратного трехчлена:
- 21. Найти область определения логарифма
- 22. ответы1) (-2;+∞)2) (-∞;1,5)3) (-∞;2) и (5;+∞)4) (-∞;-5) и (5;+∞)5) (0;3)6) (2;5)
- 23. Логарифмические уравнения
- 24. ОпределениеУравнение видаНазывается логарифмическим(а > 0, а ≠ 1; х>0)
- 25. Способы решения логарифмических уравнений: 1) по определению
- 26. При решении логарифмических уравнений помните! Необходимо найти
- 27. Примеры: 1. По определению логарифма
- 28. Слайд 28
- 29. 2. Метод приведения к одному основанию
- 30. 3. Метод введения новой переменной
- 31. 4. Сворачивание в один логарифм по свойствам
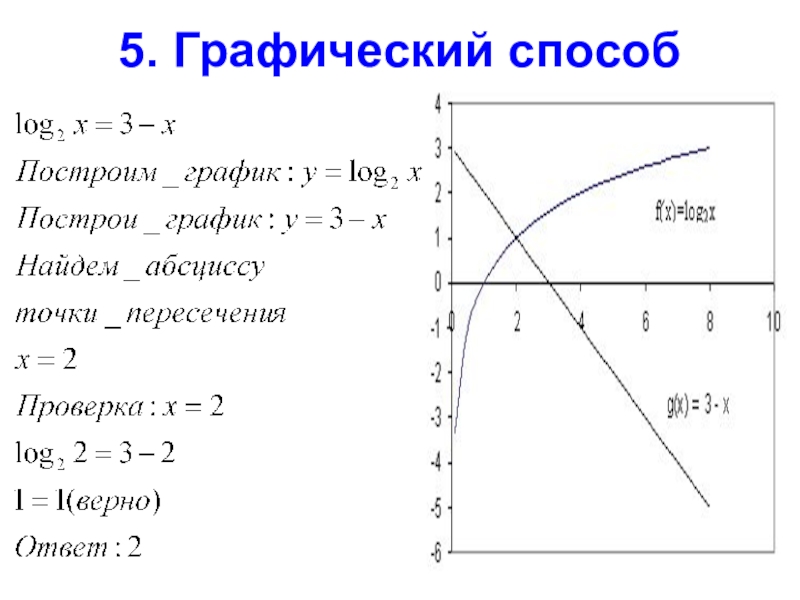
- 32. 5. Графический способ
- 33. Решить уравнение
- 34. Ответы:1) х = 272) х = 103)
- 35. Логарифмические неравенства
- 36. ОпределениеНеравенства вида:
- 37. Решение логарифмических неравенств 1) Если а>1, то
- 38. Примеры:
- 39. 2.т. к. основание
- 40. Решить неравенство
- 41. Ответы
Из истории логарифмов Немного об изобретателе логарифмов и создателе логарифмических таблиц. Джон Непер-шотландец. В 16 лет отправился на континент, где в течение 5 лет учился в различных университетах Европы, изучал математику.
Слайд 2Из истории логарифмов
Немного об изобретателе логарифмов и создателе логарифмических
таблиц.
Джон Непер-шотландец.
В 16 лет отправился на континент, где в течение 5 лет учился в различных университетах Европы, изучал математику.
Джон Непер-шотландец.
В 16 лет отправился на континент, где в течение 5 лет учился в различных университетах Европы, изучал математику.
Слайд 3 К идее логарифмических вычислений Непер пришел ещё
в 80-х годах 16 века, однако опубликовал свои таблицы только в 1614г.,после 25-летних вычислений.
Они вышли под названием "Описание чудесных логарифмических таблиц".
Неперу принадлежит и сам термин логарифм, который он переводит как "искусственное число".
Они вышли под названием "Описание чудесных логарифмических таблиц".
Неперу принадлежит и сам термин логарифм, который он переводит как "искусственное число".
Слайд 4Определение логарифма: Логарифмом числа b по основанию а называется показатель степени, в которую
нужно возвести основание а, чтобы получить число b.
(т.е. logab = c, где ас = b)
где а>0, а≠1,b>0
где а>0, а≠1,b>0
Слайд 13Свойства логарифмов
При любых а>0, а ≠ 1 и любых положительных х
и у выполняются равенства:
1) loga1 = 0
2) logaa = 1
Слайд 16Определение:
Функцию, заданную формулой
у = logaf(x) называют логарифмической
функцией с основанием а,
где а>0, а≠1,
Свойства логарифмической
функции:
D(loga) = R+
f(x) > 0
2. E(loga) = R
Свойства логарифмической
функции:
D(loga) = R+
f(x) > 0
2. E(loga) = R
Слайд 184. Графики показательной и логарифмической функций, имеющих одинаковое основание, симметричны относительно
прямой у=х
Слайд 19Примеры
Найти область определения функции:
1.
Область определения логарифмической функции- множество
Поэтому данная функция определена
для тех х, при которых
4 – 5х>0
-5x > -4
x< -4 :(-5)
x< 0,8
Ответ: ( -∞; 0,8)
4 – 5х>0
-5x > -4
x< -4 :(-5)
x< 0,8
Ответ: ( -∞; 0,8)
Слайд 25Способы решения логарифмических уравнений:
1) по определению логарифма
2) методом приведения к одному
основанию
3) методом введения новой переменной
4) сворачиванием в один логарифм по
свойствам
5) Графический метод
Слайд 26При решении логарифмических уравнений помните!
Необходимо найти ОДЗ уравнения или сделать
проверку соответствия найденных корней ОДЗ данного уравнения.
Слайд 37Решение логарифмических неравенств
1) Если а>1, то
logaf(x) > logag(x) <=>
2) Если 0< а<1, то
logaf(x) > logag(x) <=>