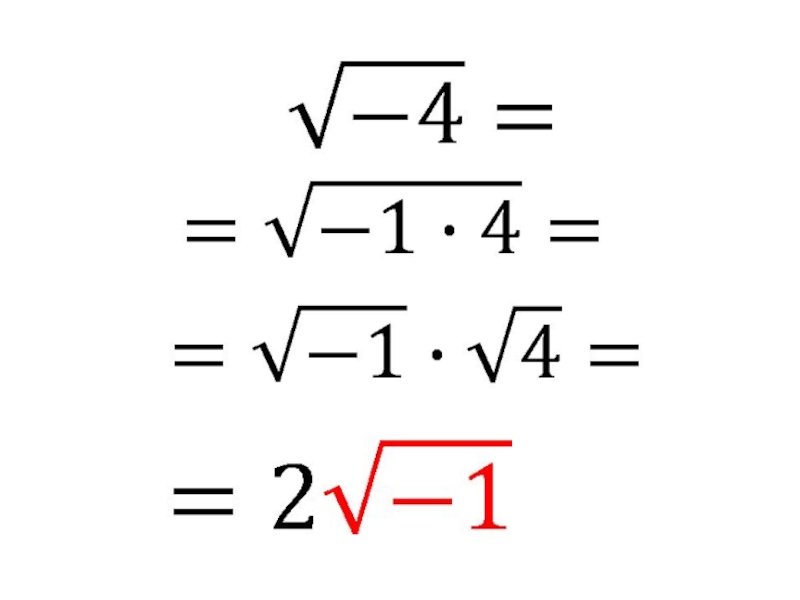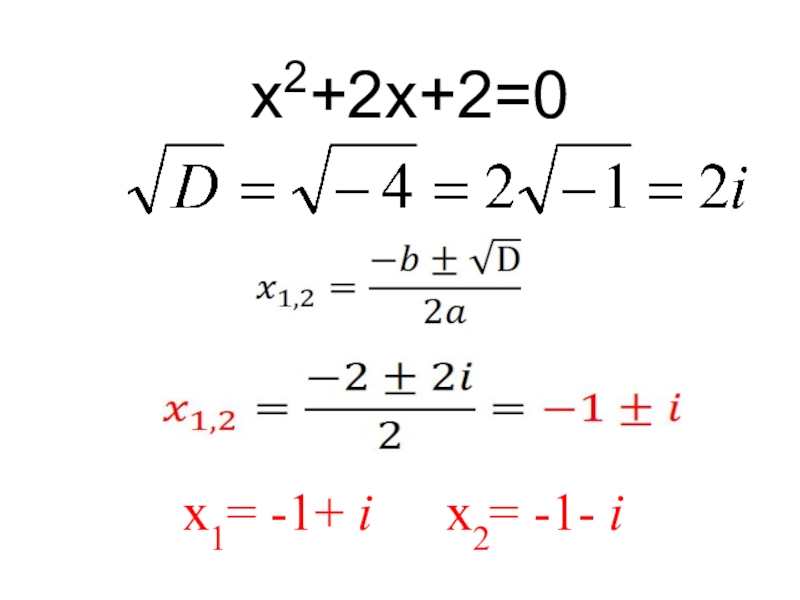- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Комплексные числа
Содержание
- 1. Презентация по математике на тему Комплексные числа
- 2. 1-6+5=0x1=1; x2=5Решите уравнение:х2-6х+5=0
- 3. (2x+1)2=02x+1=0x=-0,5Решите уравнение:4х2+4х+1=0
- 4. D=22-4∙1∙2= - 4 D< 0, корней нетРешите уравнение:х2+2х+2=0
- 5. Слайд 5
- 6. - комплексное число- мнимая единица= i= 2iМнимая
- 7. Мнимая единицаi – начальная буква французского слова imaginaire – «мнимый»
- 8. х2+2х+2=0x2= -1- ix1= -1+ i
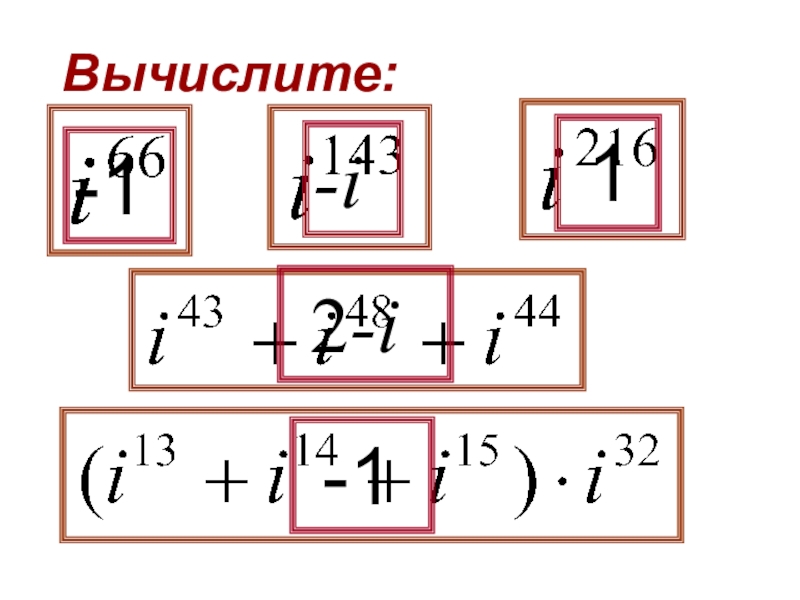
- 9. Например,Вычислите:
- 10. Комплексные числа Определение. Числа вида a +
- 11. VII в.н.э.-квадратный корень из положительного числа имеет
- 12. В XVI векев связи с изучением
- 13. Он предложил
- 14. в 1572 году итальянский учёный Бомбелли выпустил
- 15. Название “мнимые числа” ввёл
- 16. один из крупнейших математиков
- 17. гораздоВ настоящее время в математикешире,комплексные числаиспользуются действительные чем
- 18. Комплексные числа имеют прикладное значение во многих
- 19. Символический метод расчета цепей переменного токаИзменение тока
- 20. Методы операционного исчисления
- 21. Переменный ток и бытовая техника Все электропотребляющие
- 22. Применяются при
- 23. При вычерчивании географических карт
- 24. В исследовании
- 25. ===···1(-i )1 11(-1)·
- 26. Значения степеней числа i повторяются с периодом,
- 27. Решение.
- 28. Вычислите:-1-i 1 2-i -1
- 29. Определение. z1 = a+bi
- 30. Решение. Согласно условию равенства комплексных чисел
- 31. Действия над комплексными числами СложениеВычитаниеУмножениеДеление
- 32. (а+bi)
- 33. Выполните действия: z1 =
- 34. Выполните действияЗадание:z1=2i-3z2=3-4 iz1 - z2=?z1 + z2=?z1+z2=(2i
- 35. Умножение(c+di)= acbсi=+++аdbd(а+bi)i==(ac-bd)+(аd+bc)ii2Произведением комплексных чисел является комплексное число:= acаdbсbd=++-ii
- 36. Выполните действия: (5 + 3i)(5 – 3i)
- 37. Слайд 37
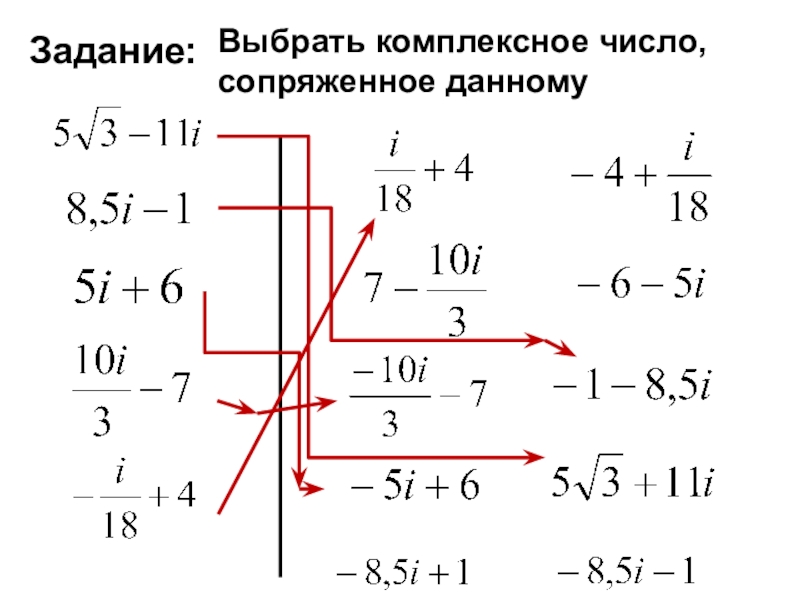
- 38. Выбрать комплексное число, сопряженное данномуЗадание:
- 39. ( 6+5i)(6-5i)=62 - (5i)2 = 62 -
- 40. Для того, чтобы разделить два комплексных числа, нужно делимое и делитель умножить на число, сопряженное делителю,т.е.Деление
- 41. ===Выполните действия:==
- 42. Выполните действиez1=2i-3z2=3-4 iz1 : z2=?==
- 43. Выполните действия:===2
- 44. Решить примеры. 2) Найти x и y
- 45. После изучения темы «Комплексные числа учащиеся должны:Знать:алгебраическую
1-6+5=0x1=1; x2=5Решите уравнение:х2-6х+5=0
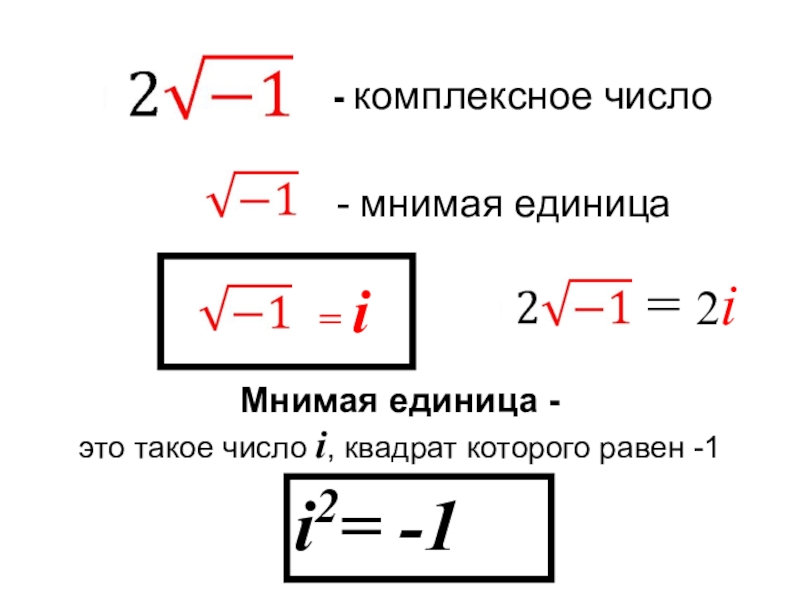
Слайд 6- комплексное число
- мнимая единица
= i
= 2i
Мнимая единица -
это такое число
i, квадрат которого равен -1
i2= -1
Слайд 10Комплексные числа
Определение. Числа вида a + bi,
где a и b – действительные числа,
i – мнимая единица,
называются комплексными.
i – мнимая единица,
называются комплексными.
a - действительная часть ,
bi – мнимая часть,
b – коэффициент при мнимой части.
Слайд 11VII в.н.э.-
квадратный корень из положительного числа имеет два значения –
положительное
и отрицательное,
а из отрицательных чисел квадратные корни извлечь нельзя:
нет такого числа х, чтобы
х2 = -9.
х2 = -9.
Слайд 12В XVI
веке
в связи с изучением
кубических уравнений
оказалось необходимым
извлекать квадратные
корни
из отрицательных чисел.
Первым учёным,
предложившим ввести
числа новой природы,
был Джорж Кордано.
из отрицательных чисел.
Первым учёным,
предложившим ввести
числа новой природы,
был Джорж Кордано.
Слайд 13Он предложил
Кордано назвал такие величины
“чисто отрицательными” или даже “софистически отрицательными”, считая их бесполезными и стремился не применять их.
Слайд 14в 1572
году
итальянский учёный
Бомбелли
выпустил книгу, в
которой были
установлены первые правила
арифметических операций над
комплексными числами,
вплоть до извлечения из них
кубических корней.
установлены первые правила
арифметических операций над
комплексными числами,
вплоть до извлечения из них
кубических корней.
Слайд 16 один из крупнейших математиков XVIII века – Л. Эйлер
предложил использовать
первую букву
французского слова
imaginare (мнимый)
для обозначения
в 1777
году
Слайд 18Комплексные
числа имеют
прикладное значение
во многих областях науки, являются
основным
аппаратом
для расчетов
в электротехнике и связи.
для расчетов
в электротехнике и связи.
Слайд 19Символический метод расчета цепей переменного тока
Изменение тока в емкости по синусоидальному
закону:
i(t) = ImC sin(ωt + ψi)
Изменение тока в индуктивности по синусоидальному закону:
i(t) = ImL sin(ωt + ψi)
Уравнение связи между током и напряжением в индуктивности:
uL = L · di / dt
i(t) = ImC sin(ωt + ψi)
Изменение тока в индуктивности по синусоидальному закону:
i(t) = ImL sin(ωt + ψi)
Уравнение связи между током и напряжением в индуктивности:
uL = L · di / dt
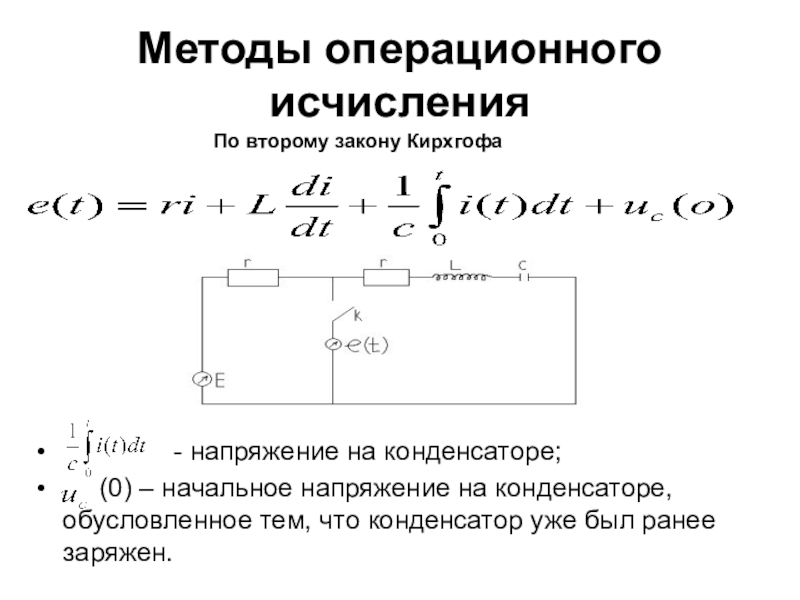
Слайд 20Методы операционного исчисления
- напряжение на конденсаторе;
(0) – начальное напряжение на конденсаторе, обусловленное тем, что конденсатор уже был ранее заряжен.
(0) – начальное напряжение на конденсаторе, обусловленное тем, что конденсатор уже был ранее заряжен.
По второму закону Кирхгофа
Слайд 21Переменный ток и бытовая техника
Все электропотребляющие устройства обладают активной и
реактивной нагрузкой.
Общая нагрузка описывается
как комплексное число:
S – полная мощность, φ - полярный угол.
Показатель cos(φ) является важным показателем работы энергосистемы и в бывшем СССР, а сегодня и в России по ГОСТ cos(φ) равен 0,8
Общая нагрузка описывается
как комплексное число:
S – полная мощность, φ - полярный угол.
Показатель cos(φ) является важным показателем работы энергосистемы и в бывшем СССР, а сегодня и в России по ГОСТ cos(φ) равен 0,8
Слайд 27 Решение.
i ,– 1, – i , 1 ,
ост. 1 2 3 без
Имеем, 28 = 4×7 (нет остатка);
33 = 4×8 + 1 ;
135 = 4×33 + 3 .
Соответственно получим
ост. 1 2 3 без
Имеем, 28 = 4×7 (нет остатка);
33 = 4×8 + 1 ;
135 = 4×33 + 3 .
Соответственно получим
Слайд 29Определение.
z1 = a+bi z2
= c+di
Комплексные числа z1 и z2 называются равными тогда и только тогда, когда равны их действительные и мнимые части
a=c, b=d
Комплексные числа z1 и z2 называются равными тогда и только тогда, когда равны их действительные и мнимые части
a=c, b=d
Слайд 30Решение. Согласно условию равенства комплексных чисел имеем 3y = 15, 5x
= – 7.
Отсюда
Найти x и y из равенства:
3y + 5xi = 15 – 7i;
Пример .
Слайд 32(а+bi)
Вычитание
=(a+c)
+
(c+di)
Сложение
(b+d)
+
i
(а+bi)
-
(c+di)
=(a-c)
+
(b-d)
i
Суммой
(разностью) двух комплексных чисел является комплексное число:
Слайд 33Выполните действия:
z1 = 2 + 3i
z2 = 5 – 7i.
Найти: а) z1 + z2; б) z1 – z2;
Найти: а) z1 + z2; б) z1 – z2;
а) z1 + z2 =(2 + 3i) + (5 – 7i) =
=2 + 5 + 3i – 7i = 7 – 4i
б) z1 – z2 =(2 + 3i) – (5 – 7i) =
=2 + 3i - 5 +7i = – 3 + 10i
Решение.
Слайд 34Выполните действия
Задание:
z1=2i-3
z2=3-4 i
z1 - z2=?
z1 + z2=?
z1+z2=(2i – 3)+(3 - 4i)=
=2i
-3+3- 4i=-2i
z1 - z2=(2i – 3) - (3 - 4i)=
=2i – 3 -3+ 4i=- 6+6i
Слайд 35Умножение
(c+di)
= ac
bс
i
=
+
+
+
аd
bd
(а+bi)
i
=
=
(ac-bd)
+
(аd+bc)
i
i2
Произведением комплексных чисел является комплексное число:
= ac
аd
bс
bd
=
+
+
-
i
i
Слайд 36Выполните действия:
(5 + 3i)(5 – 3i)
(2 + 3i)(5 –
7i)
(2 – 7i)2
=
=
=
=
=
31+i
25-9i2
=
34
4 - 28i + 49i2
=
-45-28i
Слайд 39( 6+5i)(6-5i)=
62 - (5i)2 = 62 - 52i2 = 62 +
52
Произведение сопряженных комплексных чисел равно сумме квадратов действительной части
и коэффициентов при i
Произведение сопряженных комплексных чисел равно сумме квадратов действительной части
и коэффициентов при i
(a+bi)(a-bi) = a2+b2
Слайд 40Для того, чтобы разделить два комплексных числа, нужно делимое и делитель
умножить на число, сопряженное делителю,т.е.
Деление
Слайд 44Решить примеры.
2) Найти x и y из равенства:
(2x +
3y) + (x – y)i = 7 + 6i.
1) (i63+i17+i13+i82)(i72–i34);
3)
Слайд 45После изучения темы «Комплексные числа учащиеся должны:
Знать:
алгебраическую форму комплексного числа.
Уметь:
производить над
комплексными числами операции сложения, умножения, вычитания, деления, возведения в степень, извлечение корня из комплексного числа;
в простейших случаях находить комплексные корни уравнений с действительными коэффициентами.
в простейших случаях находить комплексные корни уравнений с действительными коэффициентами.
