- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Комбинаторные задачи (9 класс)
Содержание
- 1. Презентация по математике на тему Комбинаторные задачи (9 класс)
- 2. При создании этой презентации были использованы следующие
- 3. Комбинаторика.Комбинаторика – это раздел математики, в котором
- 4. 1. Метод перебора вариантов.Пример 2Из цифр 1,
- 5. Методы перебора(дерево возможных вариантов). Пример 3Из цифр
- 6. Дерево возможных вариантов.Пример 4.«Этот вечер свободный можно
- 7. Применение дерева возможных вариантов.Пример 4.В закрытом ящике
- 8. На завтрак можно выбрать булочку, кекс, пряники
- 9. В комнате 3 лампочки. Сколько имеется различных
- 10. Семейный ужин.Пример 1.В семье 6 человек, а
- 11. 3. « Эн факториал»-n!.1•2•3•4•5•6=720Определение. Произведение подряд идущих
- 12. Пример 2.Сколькими способами 4 вора могут по одному разбежаться на все 4 стороны. 2134NOWSБанк43211•2•3•4=4!=24Их разыскивает полиция…
- 13. Расписание уроков.Пример 3.В 9 классе в среду
- 14. Перестановки и их число.Теорема о перестановках элементов
Слайд 2При создании этой презентации были использованы следующие материалы:
А. Г. Мордкович, П.
Материалы презентации «Российская академия образования. Институт педагогических исследований одарённости детей (ИПИО).Программно-методический комплекс "Элементы теории множеств и комбинаторики " для среднего и дополнительного образования. Ю.В. Михеев, А.А. Никитин, Г.А. Сапрыкина, Л.С. Шум»: слайды №23. (Ю.В. Михеев, А.А. Никитин, Г.А. Сапрыкина, Л.С. Шум»: слайды №23. (http://www.openclass.ru/dig-resource/150925Ю.В. Михеев, А.А. Никитин, Г.А. Сапрыкина, Л.С. Шум»: слайды №23. (http://www.openclass.ru/dig-resource/150925).
Картинки и изображения с сайта http://images.yandex.ru/Картинки и изображения с сайта http://images.yandex.ru/.
Слайд 3Комбинаторика.
Комбинаторика – это раздел
математики, в котором изучаются
вопросы выбора или
элементов множества в
соответствии с заданными правилами.
Комбинаторика рассматривает конечные множества.
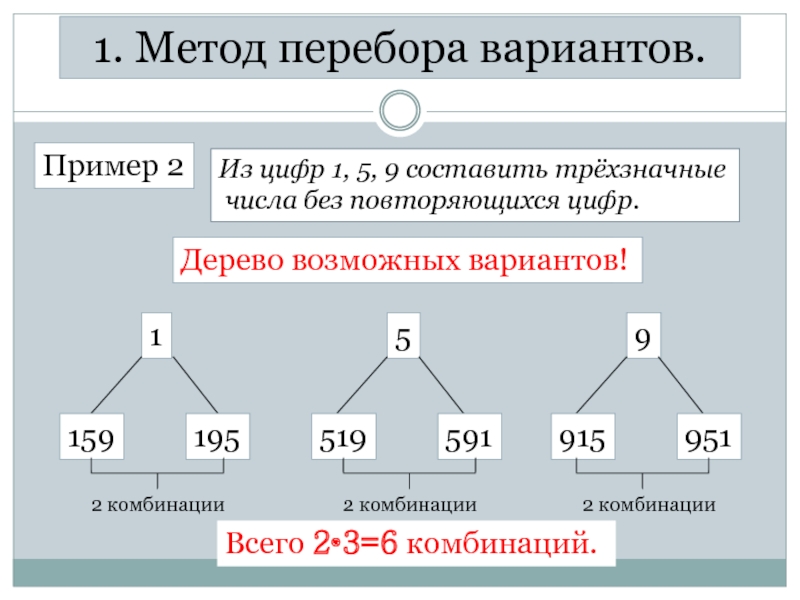
Слайд 41. Метод перебора вариантов.
Пример 2
Из цифр 1, 5, 9 составить трёхзначные
Организованный перебор!
1
159
195
5
9
519
591
915
951
2 комбинации
2 комбинации
2 комбинации
Всего 2•3=6 комбинаций.
Дерево возможных вариантов!
Слайд 5Методы перебора
(дерево возможных вариантов).
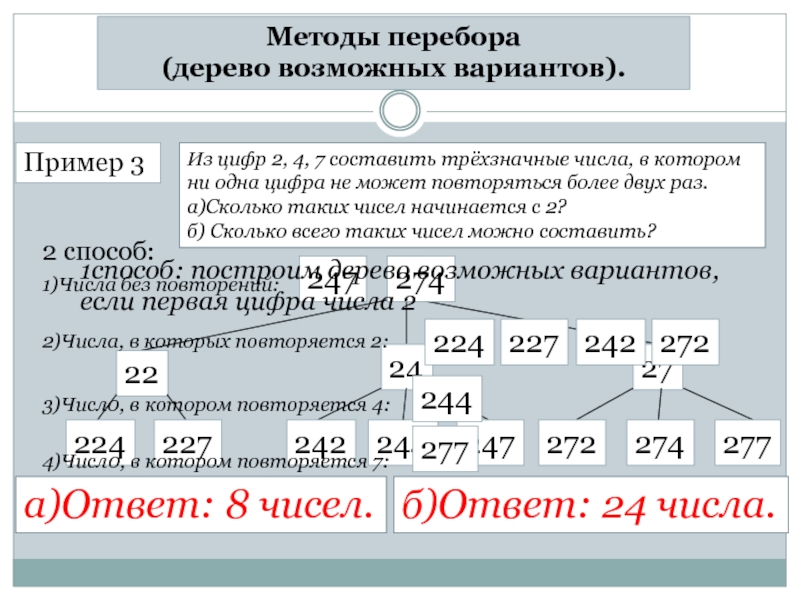
Пример 3
Из цифр 2, 4, 7 составить
ни одна цифра не может повторяться более двух раз.
а)Сколько таких чисел начинается с 2?
б) Сколько всего таких чисел можно составить?
2
24
22
27
224
227
242
247
272
277
274
244
а)Ответ: 8 чисел.
б)Ответ: 24 числа.
1)Числа без повторений:
247
274
2)Числа, в которых повторяется 2:
224
227
242
272
3)Числ0, в котором повторяется 4:
244
4)Числ0, в котором повторяется 7:
277
1способ: построим дерево возможных вариантов,
если первая цифра числа 2
2 способ:
Слайд 6Дерево возможных вариантов.
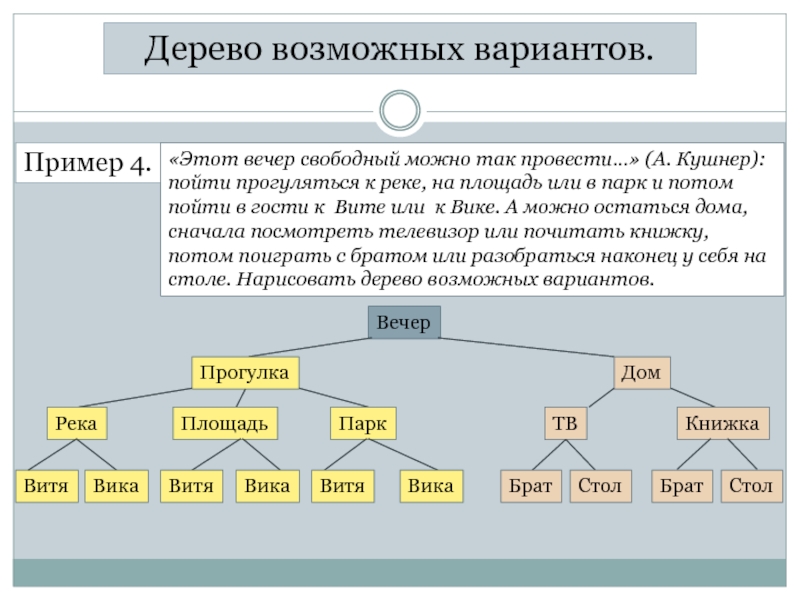
Пример 4.
«Этот вечер свободный можно так провести…» (А. Кушнер):
пойти
сначала посмотреть телевизор или почитать книжку, потом поиграть с братом или разобраться наконец у себя на столе. Нарисовать дерево возможных вариантов.
Вечер
Прогулка
Дом
Парк
Площадь
Река
Витя
Вика
Витя
Витя
Вика
Вика
ТВ
Книжка
Брат
Стол
Брат
Стол
Слайд 7Применение дерева возможных вариантов.
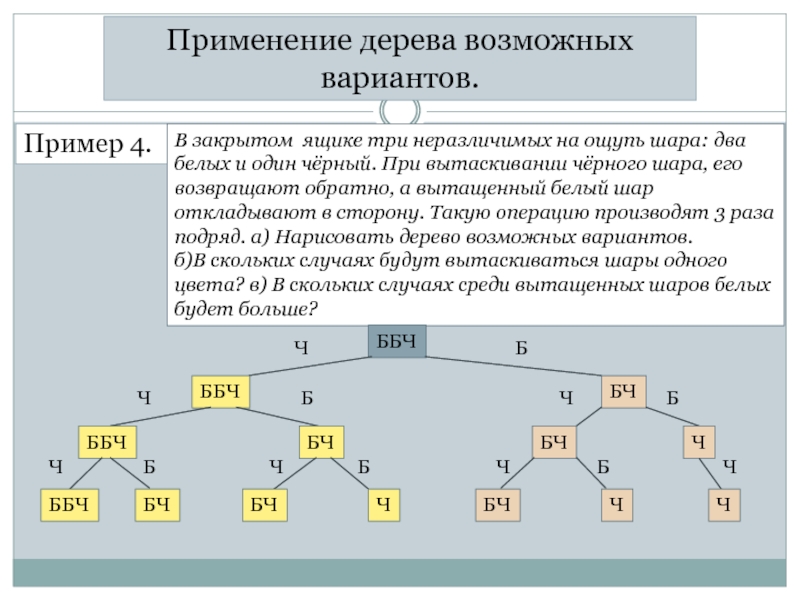
Пример 4.
В закрытом ящике три неразличимых на ощупь
белых и один чёрный. При вытаскивании чёрного шара, его возвращают обратно, а вытащенный белый шар откладывают в сторону. Такую операцию производят 3 раза подряд. а) Нарисовать дерево возможных вариантов.
б)В скольких случаях будут вытаскиваться шары одного цвета? в) В скольких случаях среди вытащенных шаров белых будет больше?
ББЧ
ББЧ
Ч
ББЧ
БЧ
Б
Ч
ББЧ
БЧ
Ч
Б
БЧ
Ч
Ч
Б
БЧ
Б
Ч
БЧ
Б
Ч
БЧ
Ч
Ч
Ч
Б
Ч
Слайд 8На завтрак можно выбрать булочку, кекс, пряники или печенье, запить можно
х/б
изд.
напитки
булочка
кекс
пряники
печенье
чай
сок
кефир
чай
чай
чай
чай
кефир
сок
сок
сок
сок
кефир
кефир
кефир
булочка
булочка
булочка
кекс
кекс
кекс
пряники
пряники
пряники
печенье
печенье
печенье
Выбор напитка- испытание А
Выбор хл./бул. изделия.- испытание В
Испытание А имеет 3 варианта (исхода), а испытание В-4, всего вариантов
независимых испытаний А и В 3•4=12.
Для того, чтобы найти число
всех возможных исходов
(вариантов) независимого
проведения двух испытаний
А и В, надо перемножить число
всех исходов испытания А на
число всех исходов испытания В
2.Правило умножения.
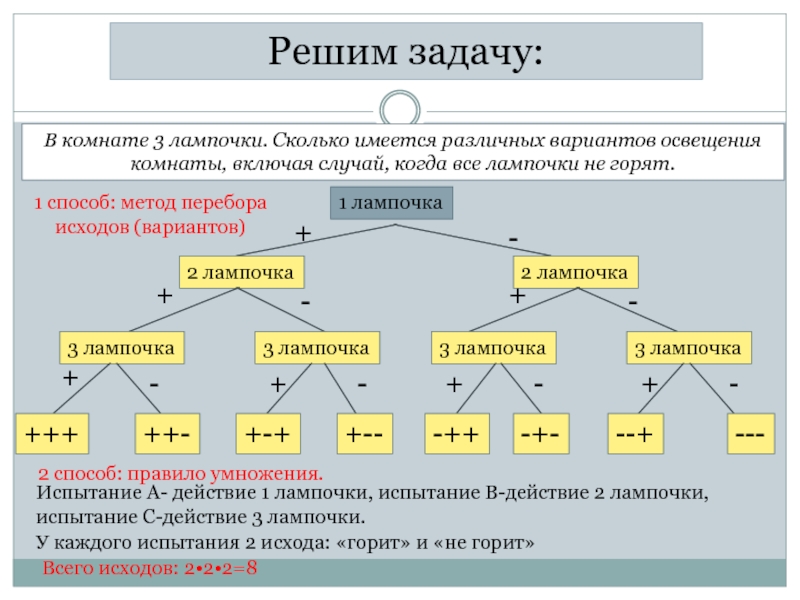
Слайд 9В комнате 3 лампочки. Сколько имеется различных вариантов освещения комнаты, включая
1 лампочка
2 лампочка
2 лампочка
+
-
+
-
3 лампочка
3 лампочка
+
-
3 лампочка
3 лампочка
+
-
+
+
+
-
+++
++-
+-+
+--
-++
-+-
--+
---
-
-
1 способ: метод перебора
исходов (вариантов)
2 способ: правило умножения.
Испытание А- действие 1 лампочки, испытание В-действие 2 лампочки,
испытание С-действие 3 лампочки.
Решим задачу:
У каждого испытания 2 исхода: «горит» и «не горит»
Всего исходов: 2•2•2=8
Слайд 10Семейный ужин.
Пример 1.
В семье 6 человек, а за столом в кухне
это без повторений?
№1
№2
№3
№4
№5
№6
6
5
4
3
2
1
6•5•4•3•2•1=
720дн.
-почти 2 года
Слайд 113. « Эн факториал»-n!.
1•2•3•4•5•6=720
Определение.
Произведение подряд идущих первых n
натуральных чисел обозначают
«эн факториал»: n!=1•2•3•…•(n-1)•n.
2!=
1•2=
2
3!=
1•2•3=
6
4!=
1•2•3•4=
24
5!=
1•2•3•4•5=
6!=
120
1•2•3•4•5•6=
720
7!=
1•2•3•4•5•6•7=
5040
n!=(n-1)!•n
Удобная формула!!!
Слайд 12Пример 2.
Сколькими способами 4 вора могут по одному разбежаться на все
2
1
3
4
N
O
W
S
Банк
4
3
2
1
1•2•3•4=4!=24
Их разыскивает полиция…
Слайд 13Расписание уроков.
Пример 3.
В 9 классе в среду 7 уроков: алгебра, геометрия,
русский язык, английский язык, биология и физкультура.
Сколько вариантов расписания можно составить?
Расставляем предметы по порядку
Алгебра
7
Геометрия
6
Литература
5
Русский язык
4
Английский язык
3
Биология
2
1
Физкультура
Всего вариантов расписания
1•2•3•4•5•6•7=
=5040
7!=
Слайд 14
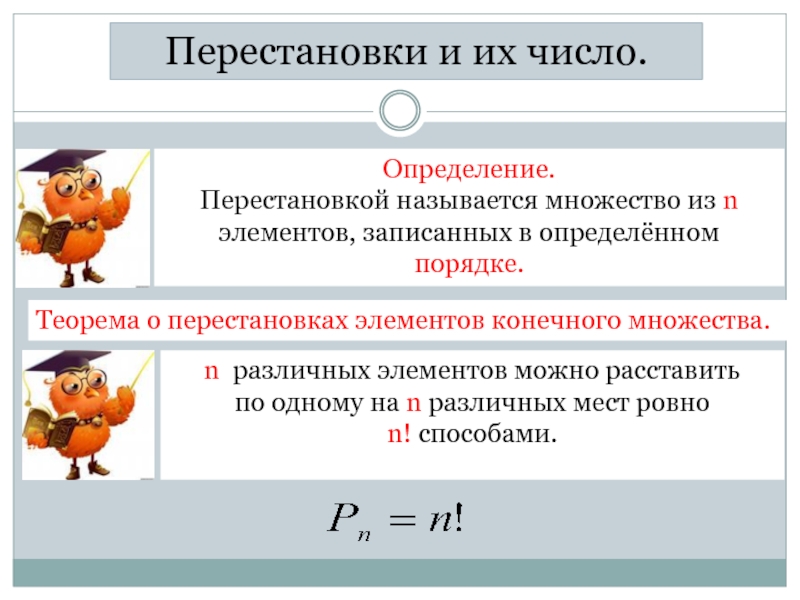
Перестановки и их число.
Теорема о перестановках элементов конечного множества.
n различных элементов
по одному на n различных мест ровно
n! способами.
Определение.
Перестановкой называется множество из n элементов, записанных в определённом порядке.