- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Исследование функций , 10 класс
Содержание
- 1. Презентация по математике на тему Исследование функций , 10 класс
- 2. Основные понятияОбласть определения - множество всех значений,
- 3. Обл.опр. Четной функции – интервал оси x,
- 4. 5.Периодические функции6.Ограниченные функцииy=f(x) – периодич.f(x+T)=f(x)T-периодy=f(x) – Ограниченная на интервале(а;b)|f(x)|0) для всех x Є (a;b)xxyyTxx+TMab-M00
- 5. 7. Точки разрыва функции и их хар-р.Точка
- 6. |||. X0 - точки бесконечного разрываAxyAxyx0x0lim f(x)=+∞,lim f(x)=A x→x0-0x→x0+0lim f(x)=+∞,lim f(x)=-∞x→x0-0x→x0+000
- 7. Прямая b называется асимптотой графика функции y=f(x),
- 8. 9. Возрастание и убывание ф-иxyx1x2abf(x2)f(x1)x1x2abf(x2)f(x1)yxy=f(x)Возрастает на интервале (a;b)x1f(x1)f(x2)Для любого x1,x2 Є(a;b)f’(x)>0 для любого xЄ (a;b) f’(x)
- 9. xyx0xyx0X0 - точка максимумаx1f(x1)f(x)f(x0)
- 10. xyx0Достаточные признаки т.экстремума Первый достаточный признакxyx0xyx0xyx0f’(x)=0 (или не существует)f’(x)>0; f’(x)
- 11. Второй достаточный признакxyx0xyx0f’(x0)=0f’’(x0)0Точка -x0 точка максимума Точка – x0 точка минимумаy00
- 12. 11. Выпуклость и вогнутость кривойxyx0xyx0Кривая выпукла на
- 13. Таблица результатовxyabxyabxyabxyabДля построения графика целесообразно проанализировать, какой
- 14. 12.Точка перегиба графика функцииДля построения точки перегиба
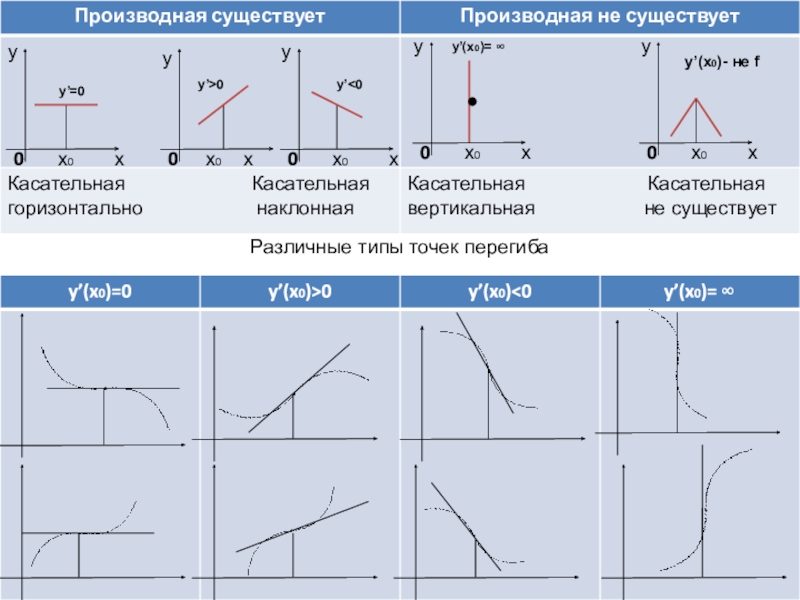
- 15. xyx00xyx00xyx00xyx00xyx00Различные типы точек перегибаy’=0 y’>0 y’
Слайд 2Основные понятия
Область определения - множество всех значений, которые может принимать аргумент,
Область значений функции: или множество значений функции. Обозначение : E(f)
Точки пересечения с осями координат: Ордината точки пересечения с 0У находится из условия y=f(0). Абсциссы точек пересечения с осью ОХ (нули функции) находятся из условия f(x)=0
Слайд 3Обл.опр. Четной функции – интервал оси x, симметричный относительно точке 0
График
Область определения нечетной функции – интервал оси Х, симметричный относительно точке 0.
График нечетной функции симметричный относительно начала координат.
Функция, не являющаяся ни четной, ни нечетной, называется функцией общего положения.
4.Четные, нечетные функции и функции общего положения:
y=f(x) –
Четная
<опр.>
f(-x)=f(x)
y=f(x) –
Нечетная
<опр.>
f(-x)=-f(x)
-х
х
f(-x) f(x)
0
-х
х
f(-x)
f(x)
x
y
y
x
0
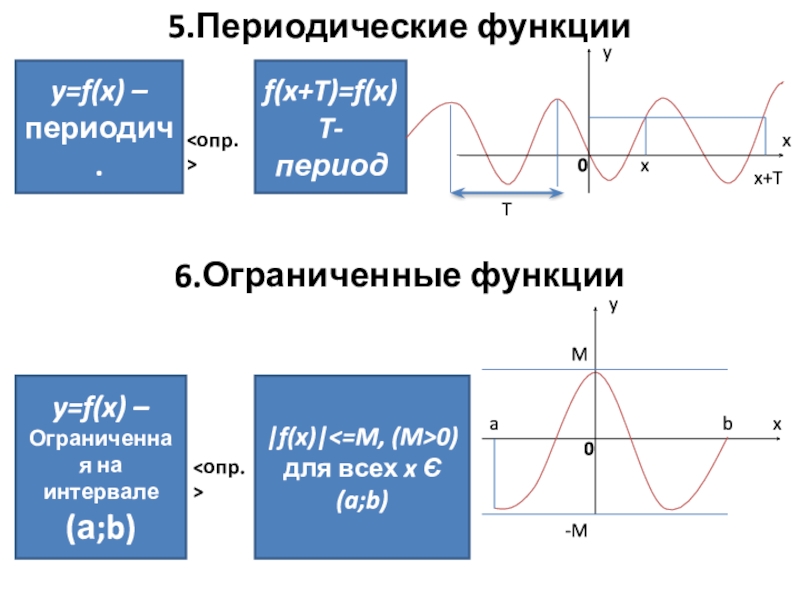
Слайд 45.Периодические функции
6.Ограниченные функции
y=f(x) –
периодич.
f(x+T)=f(x)
T-период
y=f(x) –
Ограниченная на интервале
(а;b)
|f(x)|0) для
x
x
y
y
T
x
x+T
M
a
b
-M
0
0
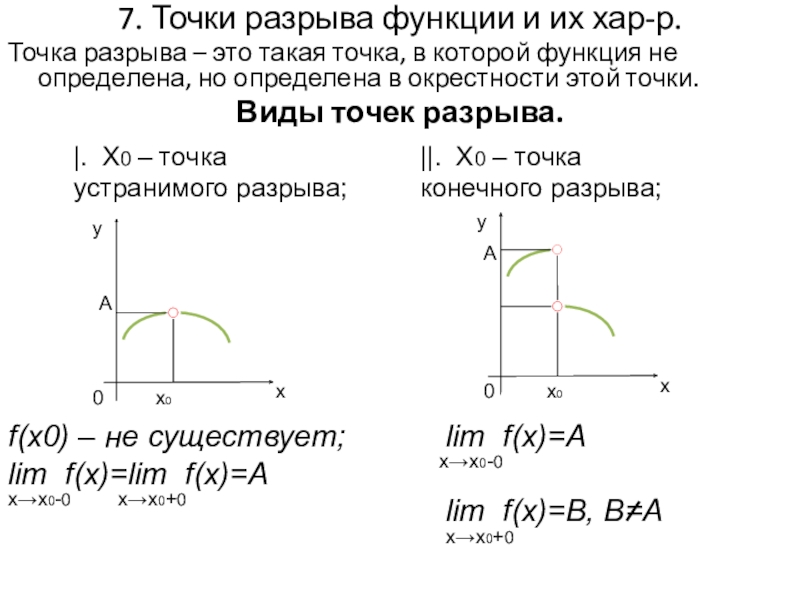
Слайд 57. Точки разрыва функции и их хар-р.
Точка разрыва – это такая
Виды точек разрыва.
x0
A
x
y
0
|. X0 – точка устранимого разрыва;
x0
A
x
y
0
||. X0 – точка конечного разрыва;
f(x0) – не существует;
lim f(x)=lim f(x)=A
x→x0-0
x→x0+0
lim f(x)=A
lim f(x)=B, B=A
x→x0-0
x→x0+0
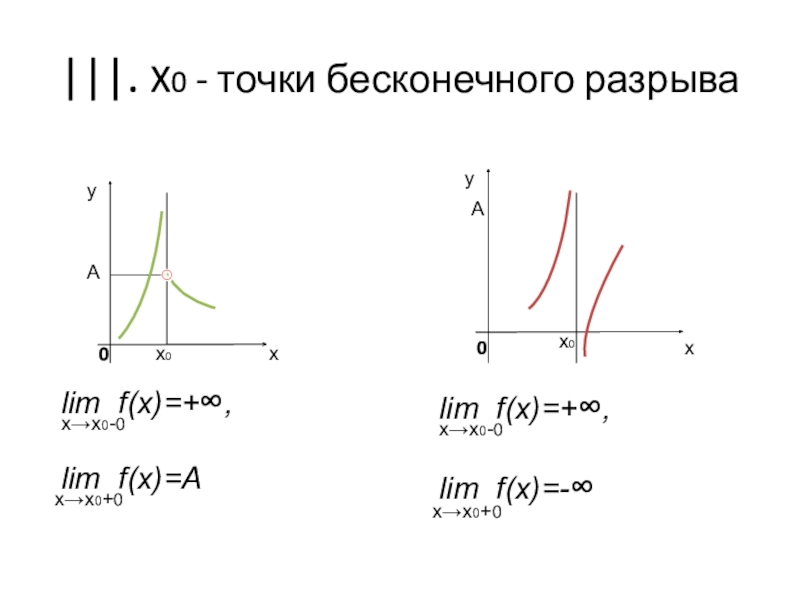
Слайд 6|||. X0 - точки бесконечного разрыва
A
x
y
A
x
y
x0
x0
lim f(x)=+∞,
lim f(x)=A
x→x0-0
x→x0+0
lim f(x)=+∞,
lim f(x)=-∞
x→x0-0
x→x0+0
0
0
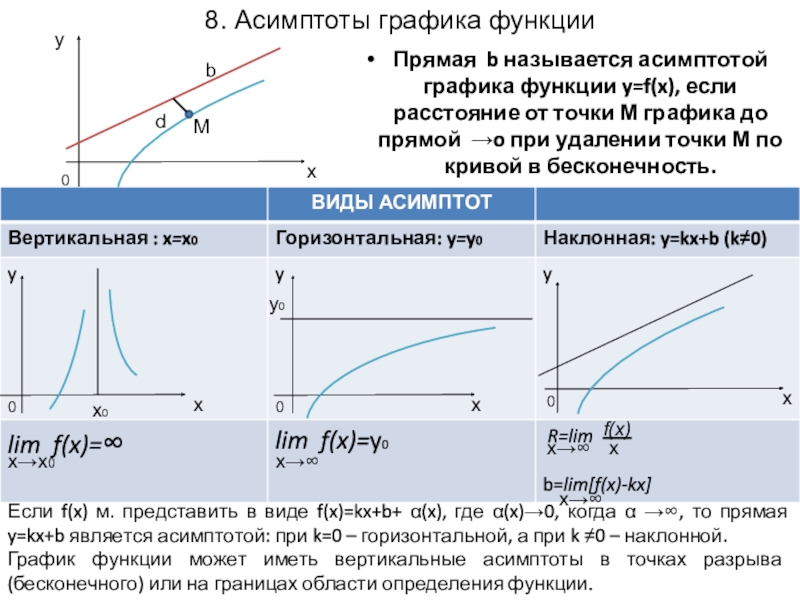
Слайд 7Прямая b называется асимптотой графика функции y=f(x), если расстояние от точки
Если f(x) м. представить в виде f(x)=kx+b+ α(x), где α(x)→0, когда α →∞, то прямая y=kx+b является асимптотой: при k=0 – горизонтальной, а при k ≠0 – наклонной.
График функции может иметь вертикальные асимптоты в точках разрыва (бесконечного) или на границах области определения функции.
8. Асимптоты графика функции
x
y
0
d
b
M
x
0
x
0
x
0
x0
y0
x→x0
x→∞
f(x)
x
x→∞
x→∞
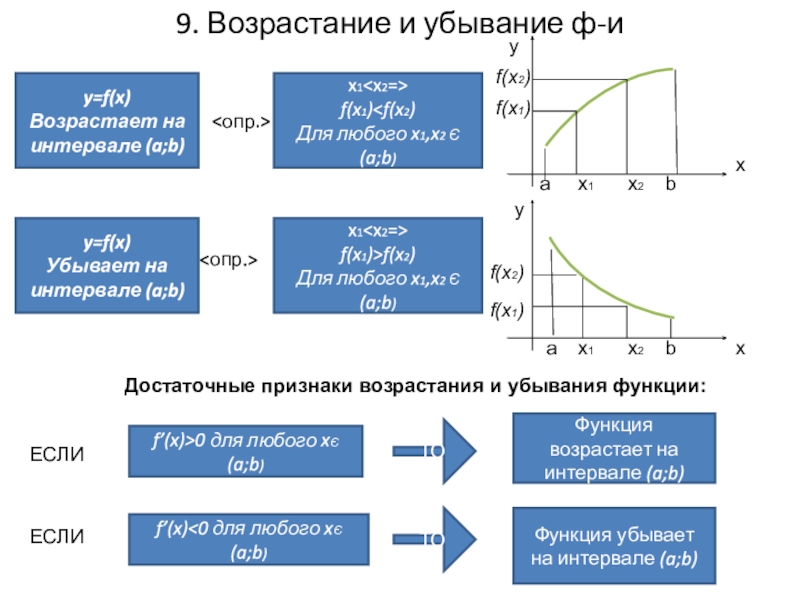
Слайд 89. Возрастание и убывание ф-и
x
y
x1
x2
a
b
f(x2)
f(x1)
x1
x2
a
b
f(x2)
f(x1)
y
x
y=f(x)
Возрастает на интервале (a;b)
x1
f(x1)
x1 f’(x)<0 для любого xЄ (a;b) Функция возрастает на интервале (a;b) Функция убывает на интервале (a;b) <опр.> <опр.> ЕСЛИ ЕСЛИ ТО ТО Достаточные признаки возрастания и убывания функции:
f(x1)>f(x2)
Для любого x1,x2 Є(a;b)
f’(x)>0 для любого xЄ (a;b)
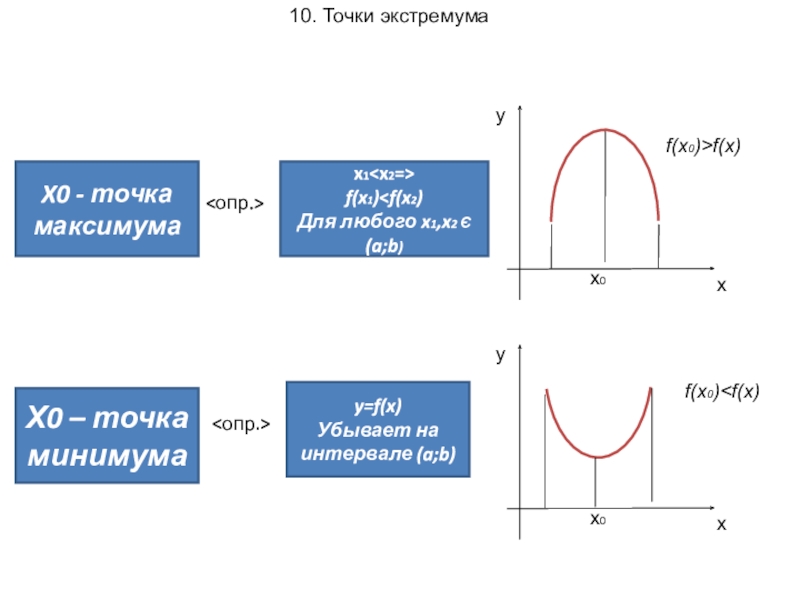
Слайд 10x
y
x0
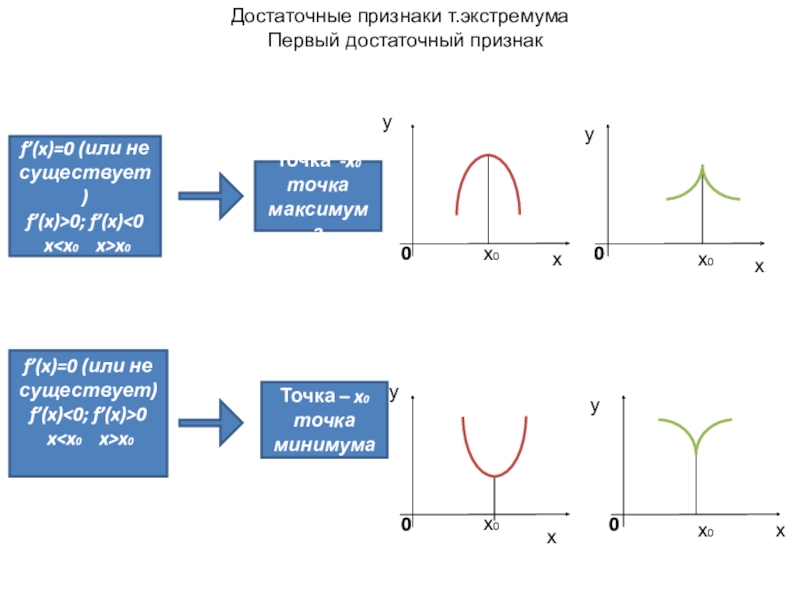
Достаточные признаки т.экстремума
Первый достаточный признак
x
y
x0
x
y
x0
x
y
x0
f’(x)=0 (или не существует)
f’(x)>0; f’(x)
f’(x)=0 (или не существует) Точка -x0 точка максимума Точка – x0 точка минимума y 0 0 0 0
f’(x)<0; f’(x)>0
x
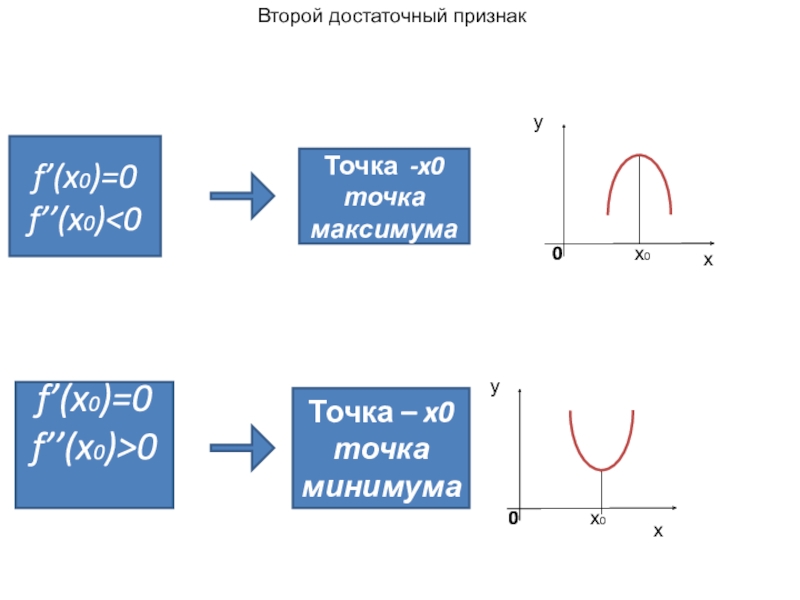
Слайд 11Второй достаточный признак
x
y
x0
x
y
x0
f’(x0)=0
f’’(x0)0
Точка -x0 точка максимума
Точка – x0 точка минимума
y
0
0
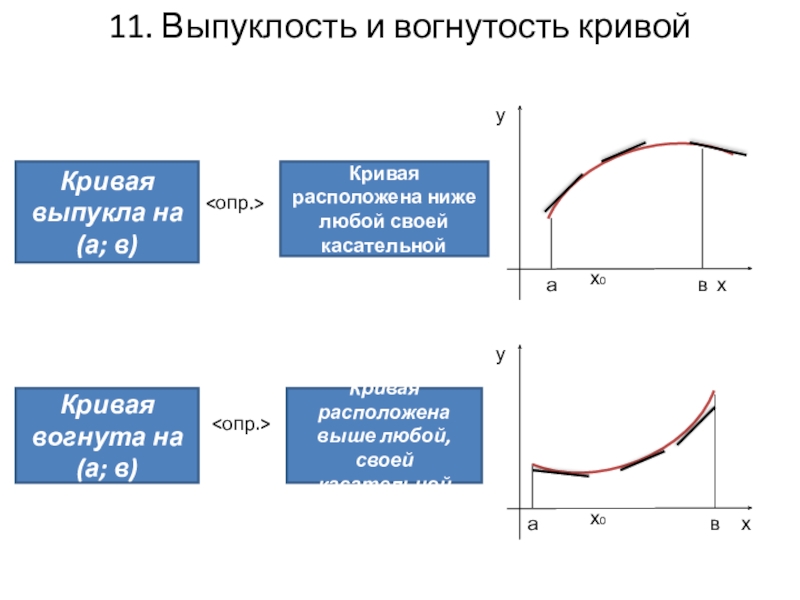
Слайд 1211. Выпуклость и вогнутость кривой
x
y
x0
x
y
x0
Кривая выпукла на (а; в)
Кривая расположена ниже
Кривая вогнута на (а; в)
<опр.>
<опр.>
Кривая расположена выше любой, своей касательной
а
в
а
в
Слайд 13Таблица результатов
x
y
a
b
x
y
a
b
x
y
a
b
x
y
a
b
Для построения графика целесообразно проанализировать, какой вид имеет график функции
Достаточные признаки выпуклости и вогнутости.
f’’(x0)>0 на (a; b)
Кривая вогнута на (a; b)
f’’(x0)<0 на (a; b)
Кривая выпукла на (a; b)
0
0
0
0
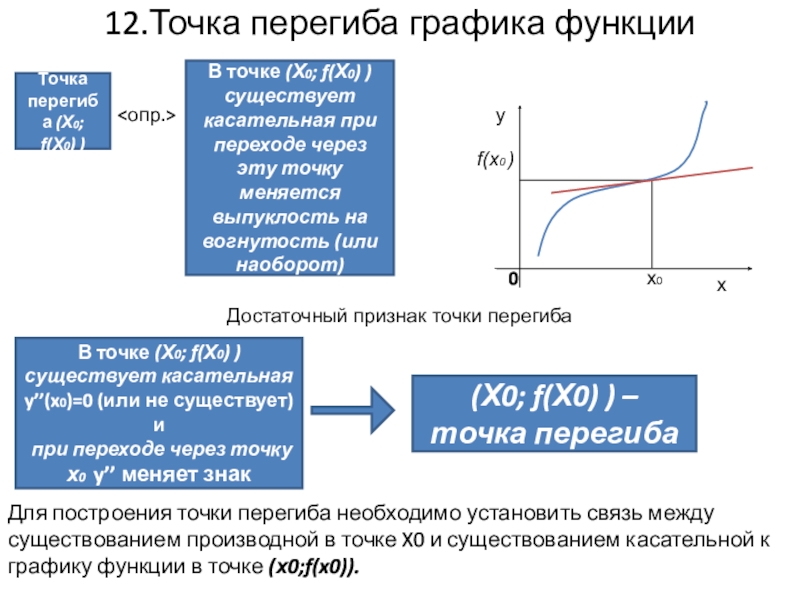
Слайд 1412.Точка перегиба графика функции
Для построения точки перегиба необходимо установить связь между
x
y
x0
Точка перегиба (Х0; f(Х0) )
В точке (Х0; f(Х0) ) существует касательная при переходе через эту точку меняется выпуклость на вогнутость (или наоборот)
<опр.>
f(x0 )
Достаточный признак точки перегиба
В точке (Х0; f(Х0) ) существует касательная y’’(x0)=0 (или не существует) и
при переходе через точку х0 y’’ меняет знак
(Х0; f(Х0) ) – точка перегиба
0