математики ВКК
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Исследование функции с помощью производной и построение графика
Содержание
- 1. Презентация по математике на тему Исследование функции с помощью производной и построение графика
- 2. План исследования функции и построения графика1. Найти
- 3. Нахождение области определения функции Обозначение: D(f)Определение: ООФ
- 4. Какие могут быть препятствия для х?
- 5. Исследование функции на четностьУсловие четности: f(x)=f(-x);
- 6. Исследование функции на периодичность
- 7. Пересечение с осями координатНули функции (пересечение с
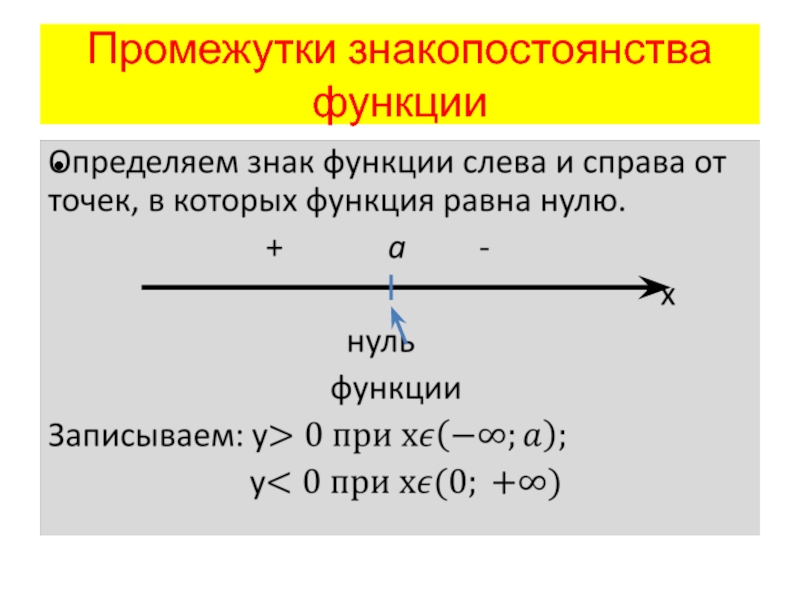
- 8. Промежутки знакопостоянства функции
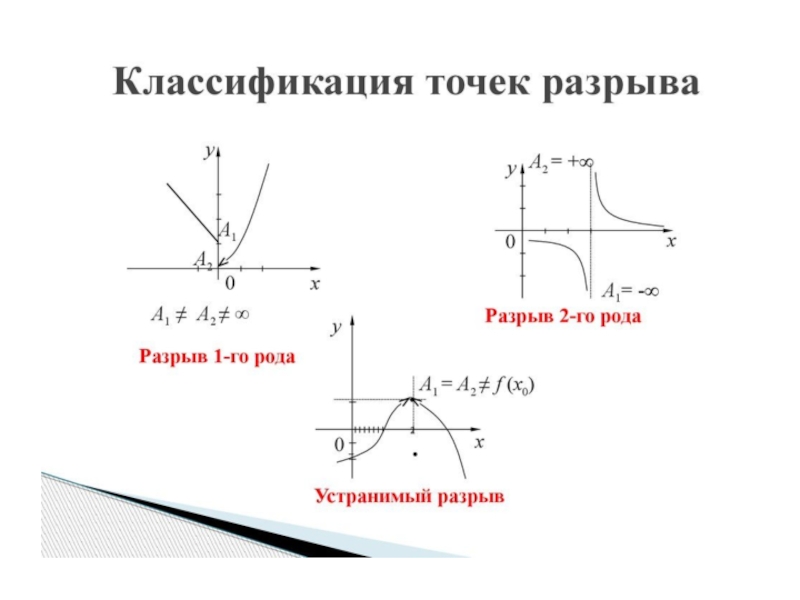
- 9. Исследование функции на непрерывность
- 10. Слайд 10
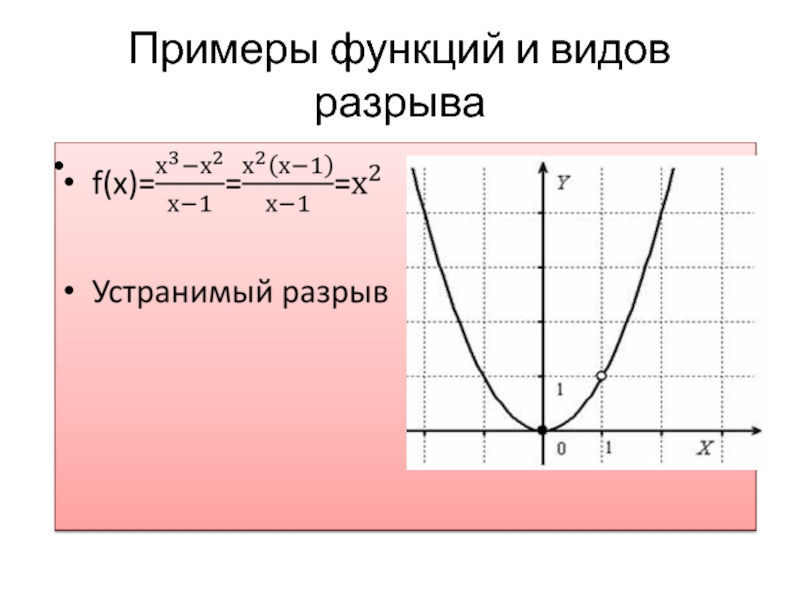
- 11. Примеры функций и видов разрыва
- 12. Функция непрерывна на всей числовой прямой кроме
- 13. Функция непрерывна на всей числовой прямой, кроме
- 14. Функция непрерывна на всей числовой прямой кроме
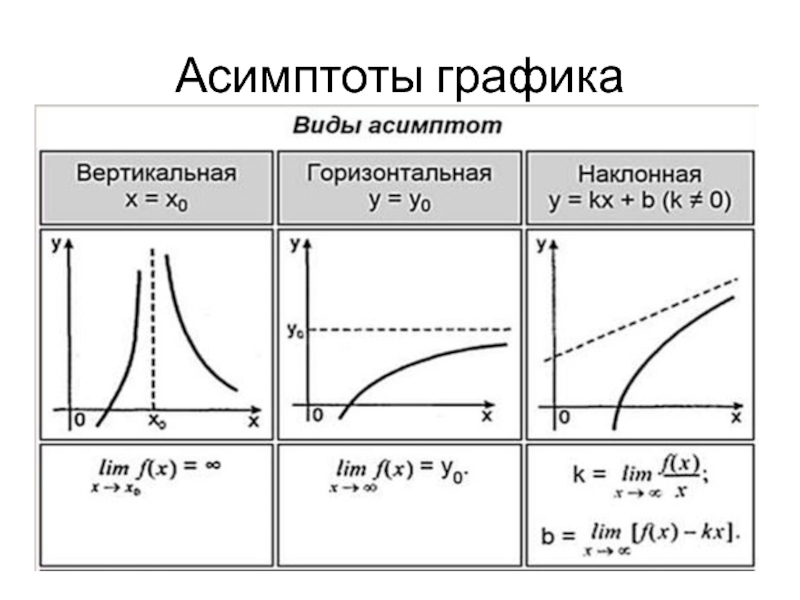
- 15. Асимптоты графика
- 16. Исследование на монотонность и экстремумыНайти производную функции.Приравнять
- 17. Исследование на выпуклость, вогнутость, перегибыНеобходимо найти вторую
- 18. Построение графикаВ процессе исследования функции мы получили
- 19. Мы определили промежутки знакопостоянства, промежутки возрастания и
- 20. Удачи в построении графика
План исследования функции и построения графика1. Найти область определения D(f) функции f(x).2. Найти область значений E(f) (если это возможно вначале, часто E(f) можно указать только по результатам исследования).3. Исследовать функцию на четность.4. Исследовать функцию на периодичность.5.
Слайд 1Исследование функции с помощью производной и построение графика функции Автор Давыдова И.М. преподаватель
Слайд 2План исследования функции и построения графика
1. Найти область определения D(f) функции
f(x).
2. Найти область значений E(f) (если это возможно вначале, часто E(f) можно указать только по результатам исследования).
3. Исследовать функцию на четность.
4. Исследовать функцию на периодичность.
5. Найти точки пересечения с осью Ox (нули функции) и точки пересечения с осью Oy.
6. Найти промежутки знакопостоянства функции.
7. Исследовать функцию на непрерывность, дать классификацию разрывов.
8. Найти асимптоты графика функции (вертикальную, наклонную, горизонтальную).
9. Исследовать функцию на монотонность и экстремум.
10. Исследовать график функции на выпуклость, вогнутость, перегиб.
11. Построить график функции.
2. Найти область значений E(f) (если это возможно вначале, часто E(f) можно указать только по результатам исследования).
3. Исследовать функцию на четность.
4. Исследовать функцию на периодичность.
5. Найти точки пересечения с осью Ox (нули функции) и точки пересечения с осью Oy.
6. Найти промежутки знакопостоянства функции.
7. Исследовать функцию на непрерывность, дать классификацию разрывов.
8. Найти асимптоты графика функции (вертикальную, наклонную, горизонтальную).
9. Исследовать функцию на монотонность и экстремум.
10. Исследовать график функции на выпуклость, вогнутость, перегиб.
11. Построить график функции.
Слайд 3Нахождение области определения функции
Обозначение: D(f)
Определение: ООФ – это множество чисел,
на котором задается функция. Если ООФ не указана, то считается, что ООФ состоит из всех значений х, при которых функция определена.
Слайд 5Исследование функции на четность
Условие четности:
f(x)=f(-x); график симметричен относительно ОY.
Условие
нечетности:
f(-x)= - f(x); график симметричен относительно начала координат.
Если эти условия не выполняются, то функция общего вида.
f(-x)= - f(x); график симметричен относительно начала координат.
Если эти условия не выполняются, то функция общего вида.
Слайд 7Пересечение с осями координат
Нули функции (пересечение с ОХ)
Решаем
уравнение f(х)=0
Пересечение с ОУ
Находим f(0)
Пересечение с ОУ
Находим f(0)
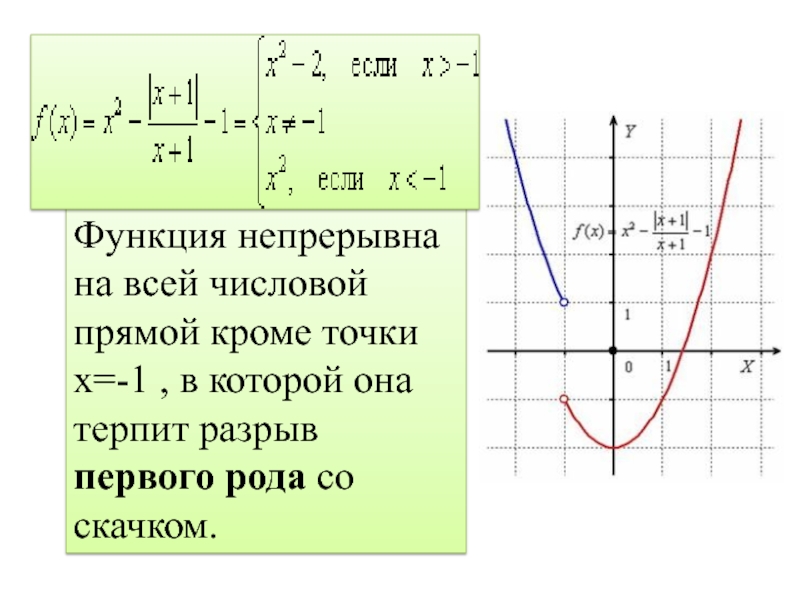
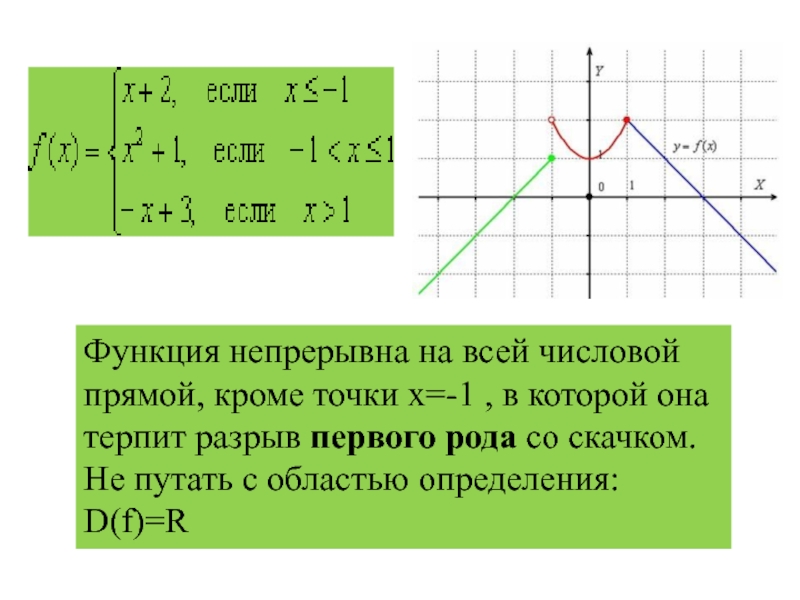
Слайд 12Функция непрерывна на всей числовой прямой кроме точки х=-1 , в
которой она терпит разрыв первого рода со скачком.
Слайд 13Функция непрерывна на всей числовой прямой, кроме точки х=-1 , в
которой она терпит разрыв первого рода со скачком.
Не путать с областью определения: D(f)=R
Не путать с областью определения: D(f)=R
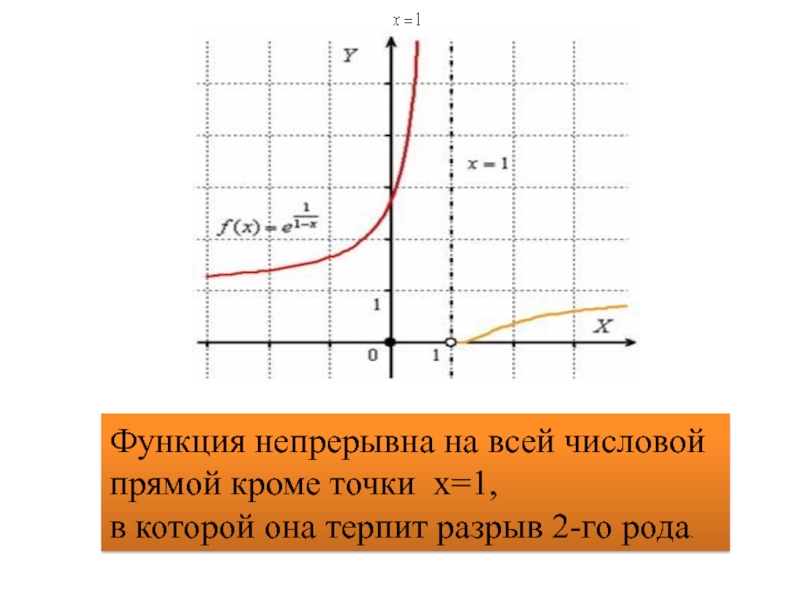
Слайд 14Функция непрерывна на всей числовой
прямой кроме точки х=1,
в которой
она терпит разрыв 2-го рода.
Слайд 16Исследование на монотонность и экстремумы
Найти производную функции.
Приравнять ее к 0.
Справа и
слева от точек, в которых производная равна нулю, определить знак производной.
Найти промежутки возрастания и убывания функции. Если производная положительна, то функция возрастает; если отрицательна, то убывает.
Найти точки экстремума (или точки перегиба)
Найти значение функции в точках экстремума или точках перегиба (для построения графика).
Найти промежутки возрастания и убывания функции. Если производная положительна, то функция возрастает; если отрицательна, то убывает.
Найти точки экстремума (или точки перегиба)
Найти значение функции в точках экстремума или точках перегиба (для построения графика).
Слайд 17Исследование на выпуклость, вогнутость, перегибы
Необходимо найти вторую производную функции и приравнять
ее к нулю. Если вторая производная больше нуля, то на этом промежутке выпуклость вниз, если меньше – выпуклость вверх. Точка, в которой вторая производная равна нулю, является точкой перегиба. В ней меняется направление выпуклости.
Слайд 18Построение графика
В процессе исследования функции мы получили следующие точки графика:
Точки пересечения
с осями
Точки максимума и минимума
Точки перегиба
Точки разрыва
Точки максимума и минимума
Точки перегиба
Точки разрыва
Слайд 19Мы определили промежутки знакопостоянства, промежутки возрастания и убывания, промежутки выпуклости и
вогнутости.
Наконец, у нас есть информация о наличии или отсутствии асимптот.
Если этих точек недостаточно, задаем нужное значение х и считаем значение функции в этой точке.
СТРОИМ ГРАФИК.
Наконец, у нас есть информация о наличии или отсутствии асимптот.
Если этих точек недостаточно, задаем нужное значение х и считаем значение функции в этой точке.
СТРОИМ ГРАФИК.