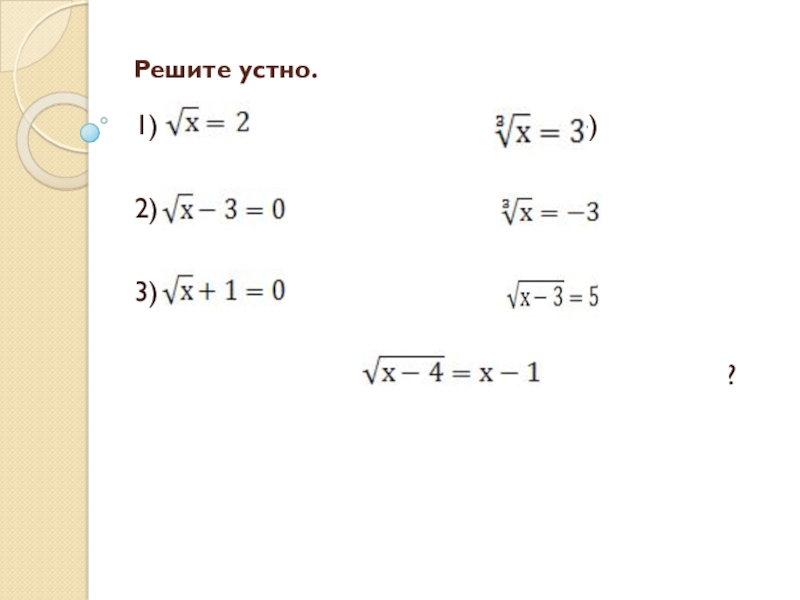Республики
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Иррациональные уравнения (10 класс)
Содержание
- 1. Презентация по математике на тему Иррациональные уравнения (10 класс)
- 2. Решите устно.1)
- 3. Иррациональные уравнения
- 4. Иррациональным уравнением называется уравнение, содержащее неизвестное под знаком корня.К простейшим иррациональным уравнениям относятся уравнения вида:
- 5. Способы решения иррациональных уравненийГлавный способ освободится от
- 6. Решите уравнение.
- 7. Решите уравнение.Ответ: х=2, х=3
- 8. Пример 1 . Решите уравнение
- 9. Пример 1 . Решите уравнение .Решение. Возведем
- 10. Классная работа№154 2) с комментарием у доски№152 1), №153 1)
- 11. Способ возведения обеих частей уравнения в одну
- 12. Метод равносильных преобразований
- 13. Пример . Решить уравнение
- 14. Пример . Решить уравнение Решение. Это уравнение
- 15. Классная работа№155 3) с комментарием№155 1)
- 16. Метод равносильных преобразованийВывод: При решении иррациональных уравнений
- 17. Самостоятельная работаВариант 1. Решите уравнение :1) с
- 18. Домашняя работа№№ 152 -155
- 19. Спасибо!Спасибо за внимание !
Решите устно.1) 4)
Слайд 1Муниципальное бюджетное общеобразовательное учреждение «Средняя общеобразовательная школа №12» города Чебоксары Чувашской
Слайд 4Иррациональным уравнением называется уравнение, содержащее неизвестное под знаком корня.
К простейшим иррациональным
уравнениям относятся уравнения вида:
Слайд 5Способы решения иррациональных уравнений
Главный способ освободится от корня и получить рациональное
уравнение - возведение обеих частей уравнения в одну и ту же степень, которую имеет корень, содержащий неизвестное, и последующее "освобождение" от корня по формуле
Если обе части иррационального уравнения возвести в одну и ту же нечетную степень и освободиться от корня, то получится уравнение, равносильное исходному
При возведении уравнения в четную степень получится уравнение, являющееся следствием исходного.
Если обе части иррационального уравнения возвести в одну и ту же нечетную степень и освободиться от корня, то получится уравнение, равносильное исходному
При возведении уравнения в четную степень получится уравнение, являющееся следствием исходного.
Слайд 9Пример 1 . Решите уравнение .
Решение. Возведем обе части этого уравнения
в квадрат и получим ,
,
откуда следует, что или .
Проверка. : .
Это неверное числовое равенство, значит, число -5 не является корнем данного уравнения.
, .
Это верное числовое равенство, значит, число -1 является корнем данного уравнения.
Ответ: Х=-1 .
,
откуда следует, что или .
Проверка. : .
Это неверное числовое равенство, значит, число -5 не является корнем данного уравнения.
, .
Это верное числовое равенство, значит, число -1 является корнем данного уравнения.
Ответ: Х=-1 .
Слайд 11Способ возведения обеих частей уравнения в одну и ту же степень
Вывод:
При
решении иррациональных уравнений методом возведения обеих частей уравнения в одну и туже степень необходимо вести словесную запись, что делает решение понятным и доступным. Однако обязательная проверка иногда бывает громоздкой и занимает много времени. Этот метод можно использовать для несложных иррациональных уравнений, содержащих 1-2 радикала.
Слайд 14Пример . Решить уравнение
Решение. Это уравнение равносильно системе
Решая первое уравнение
этой системы, равносильное уравнению
получим корни х=1, х=-2.
Второй корень х=-2 не удовлетворяет неравенству системы и, следовательно, является посторонним корнем исходного уравнения.
Ответ: х=1
получим корни х=1, х=-2.
Второй корень х=-2 не удовлетворяет неравенству системы и, следовательно, является посторонним корнем исходного уравнения.
Ответ: х=1
Слайд 16Метод равносильных преобразований
Вывод: При решении иррациональных уравнений методом равносильных преобразований не
нужно опасаться потеря корней и приобретения посторонних корней. Не нужно проверять полученные решения с помощью подстановки в исходное уравнение.
Слайд 17Самостоятельная работа
Вариант 1. Решите уравнение :
1) с помощью возведения в квадрат
2)
Методом равносильного преобразования
Допол. задание №152 3)
Вариант 2. Решите уравнение :
1) с помощью возведения в квадрат
2)Методом равносильного преобразования
Допол. задание №153 3)
Ответ: В1. 1) 2; 2) 6. В2. 1) 4; 2) -2
Допол. задание №152 3)
Вариант 2. Решите уравнение :
1) с помощью возведения в квадрат
2)Методом равносильного преобразования
Допол. задание №153 3)
Ответ: В1. 1) 2; 2) 6. В2. 1) 4; 2) -2