- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Иррациональные неравенства и способы их решения (11 класс)
Содержание
- 1. Презентация по математике на тему Иррациональные неравенства и способы их решения (11 класс)
- 2. .Иррациональные неравенства и способы их решения
- 3. Занятие №2.Занятие №1.Занятие №3.Занятие №4.
- 4. Повторение.Занятие №5.Повторение.Контрольный тест.
- 5. Занятие №1.
- 6. Поэтому данное неравенство равносильно следующей системе неравенств.1.Рассмотрим
- 7. Слайд 7
- 8. Пример 1.Решить неравенство
- 9. Тогда, решением заданного неравенства будет пересечение множеств решений системы
- 10. 2.Рассмотрим неравенство вида: Решение. ОДЗ неизвестного будет
- 11. В случае же
- 12. Слайд 12
- 13. Пример 2. Решить неравенство: Рассмотрим два случая:
- 14. Занятие №2Цель: Рассмотреть неравенства вида:При решении иррациональных
- 15. 1.Неравенство вида равносильно системе неравенств: 2.Неравенство видаравносильно неравенству f(x)
- 16. Слайд 16
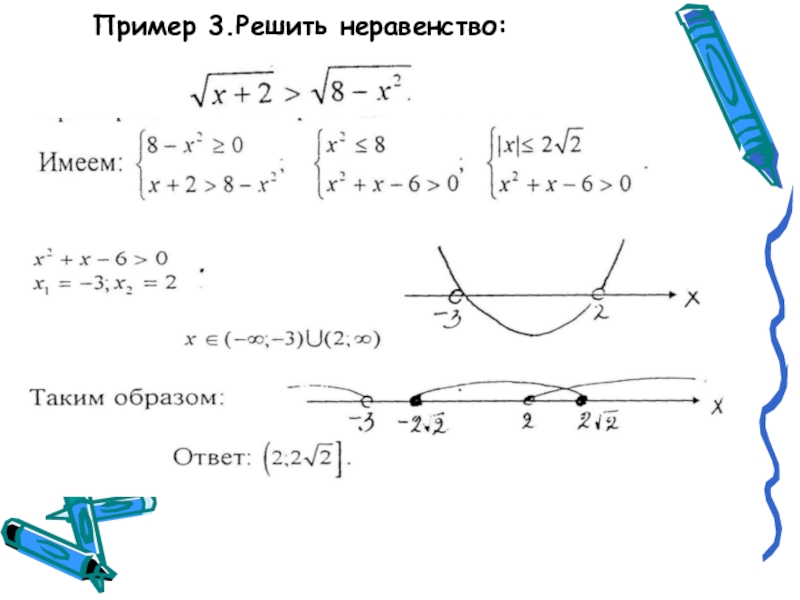
- 17. Пример 3.Решить неравенство:
- 18. Слайд 18
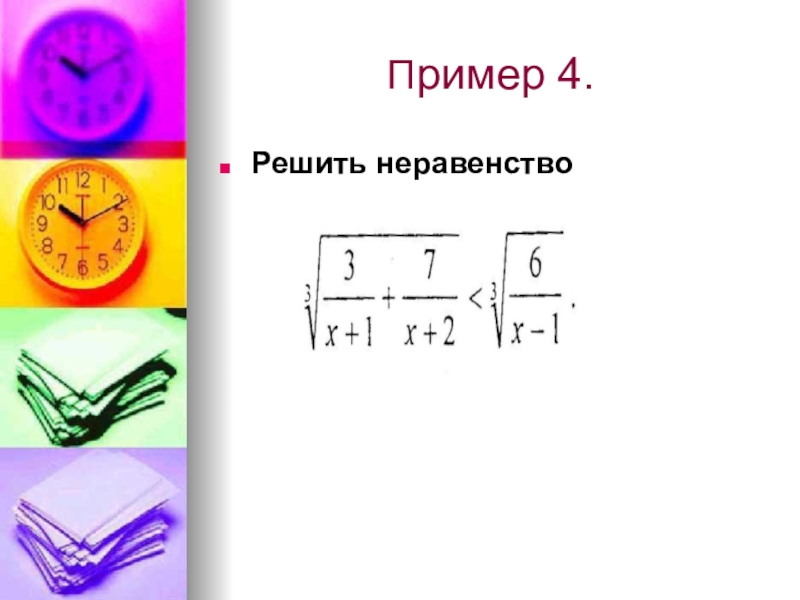
- 19. Пример4.Решить неравенство:
- 20. Занятие №3.Цель: Рассмотреть решения неравенств методом интервалов.
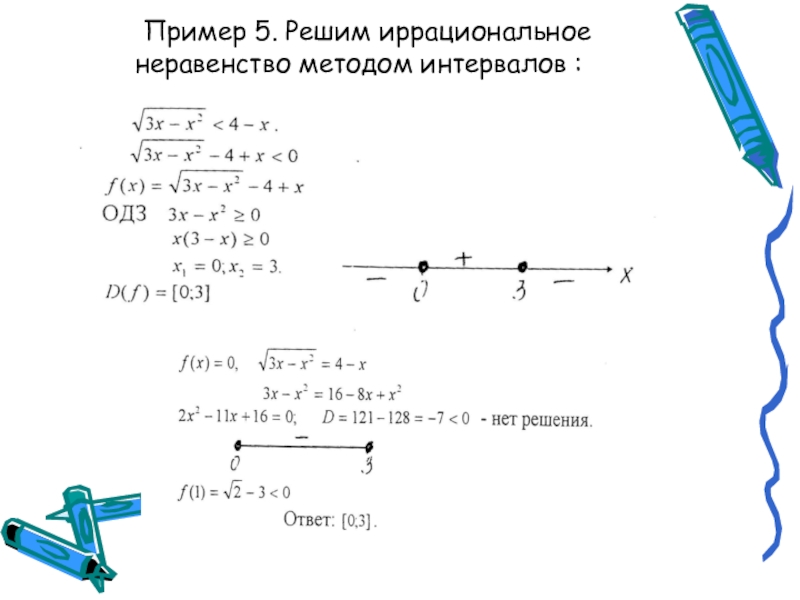
- 21. Пример 5. Решим иррациональное
- 22. Занятие №4.Цель: Рассмотреть решения иррациональных неравенств введением новой переменной
- 23. Пример 6. Решим неравенство введением новой переменной
- 24. ешим неравенствопеременно
- 25. Занятие №5.Цель: Рассмотреть решения иррациональных неравенств методом замены множителя .
- 26. Пример №7. Решим неравенство методом замены множителя
- 27. ТЕСТЗАДАНИЕ 1:Решите неравенствоЗАДАНИЕ 2:Решите неравенствоЗАДАНИЕ 3:Решите неравенство
- 28. ТЕСТЗАДАНИЕ 1:Решите неравенствоВарианты ответов:А) [-18;А) [-18;-А) [-18;-2)А)
- 29. Молодцы!!!
- 30. Слайд 30
- 31. Молодцы!!!
- 32. Слайд 32
- 33. Молодцы!!!
- 34. Домашнее задание. Решить неравенство:Пример 1. Пример 3.Пример 2.Пример 4.Пример 5.
- 35. .Иррациональные неравенства и способы их решения
- 36. Слайд 36
- 37. ОТМЕТКИ ЗА
- 38. СПАСИБО ЗА УРОК!
Слайд 5Занятие №1.
Основным
Чтобы избежать ошибок при решении иррациональных неравенств, следует рассматривать только те значения переменной, при которых все входящие в неравенство функции определены, т.е. найти ОДЗ этого неравенства, а затем обоснованно осуществлять равносильный переход на всей ОДЗ или ее частях.
Цель: Рассмотреть неравенства вида:
Слайд 6
Поэтому данное неравенство равносильно следующей системе неравенств.
1.Рассмотрим иррациональное неравенство вида
Решение. ОДЗ
К тому же, (x)>0, т.к
Слайд 102.Рассмотрим неравенство вида:
Решение. ОДЗ неизвестного будет определяться из условия
Но, в отличие от предыдущего, (x) может принимать как положительные, так и отрицательные значения. Поэтому в процессе решения должны рассматривать два случая: (x) <0 и (x) . В первом случае данное неравенство равносильно следующей системе неравенств:
Но в этой системе можно опустить последнее неравенство, т.к.
при (x)<0 оно выполняется всегда. Т.о. имеем
Слайд 11
В случае же
Заданное неравенство равносильно следующей системе неравенств:
Тогда, из
Решением неравенства будет объединение множеств решений обоих случаев.
Слайд 14Занятие №2
Цель: Рассмотреть неравенства вида:
При решении иррациональных неравенств используются те же
Слайд 151.Неравенство вида
равносильно системе неравенств:
2.Неравенство вида
равносильно неравенству f(x)
Слайд 20Занятие №3.
Цель: Рассмотреть решения неравенств методом интервалов.
При решении иррациональных неравенств
Слайд 28ТЕСТ
ЗАДАНИЕ 1:Решите неравенство
Варианты ответов:
А) [-18;А) [-18;-А) [-18;-2)А) [-18;-2) Б) (-2А) [-18;-2)
Слайд 30
Задание 2: Решите неравенство
Варианты ответов:
А) [-7;2)А) [-7;2) Б) (А) [-7;2) Б) (7;2)А) [-7;2) Б) (7;2) В) [7;А) [-7;2) Б) (7;2) В) [7;4А) [-7;2) Б) (7;2) В) [7;4]А) [-7;2) Б) (7;2) В) [7;4] Г) [-7;-2]
Слайд 32
Задание 3: Решите неравенство
Варианты ответов:
А) RА) R Б) (1А) R Б) (1;3]А) R Б) (1;3] В) (1А) R Б) (1;3] В) (1;А) R Б) (1;3] В) (1;4А) R Б) (1;3] В) (1;4]А) R Б) (1;3] В) (1;4] Г) (1;3)
Слайд 36 ВЫВОДЫ:
возведение обеих частей неравенства в одну и ту же натуральную степень
Рассмотрели иррациональные неравенства и
способы их решения.
введение новой переменной , метод интервалов ,
метод замены множителя .