- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Функции и их свойства
Содержание
- 1. Презентация по математике на тему Функции и их свойства
- 2. При изучении явлений окружающего мира и
- 3. Функция-зависимость одной величины от другой, выраженная некоторой
- 4. Линейная функцияФункция вида y = kx +
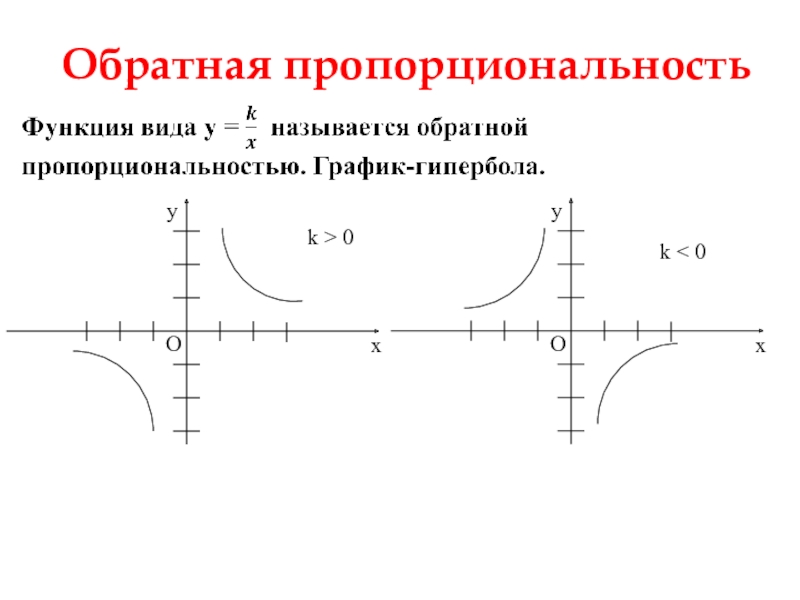
- 5. Обратная пропорциональностьk > 0k < 0
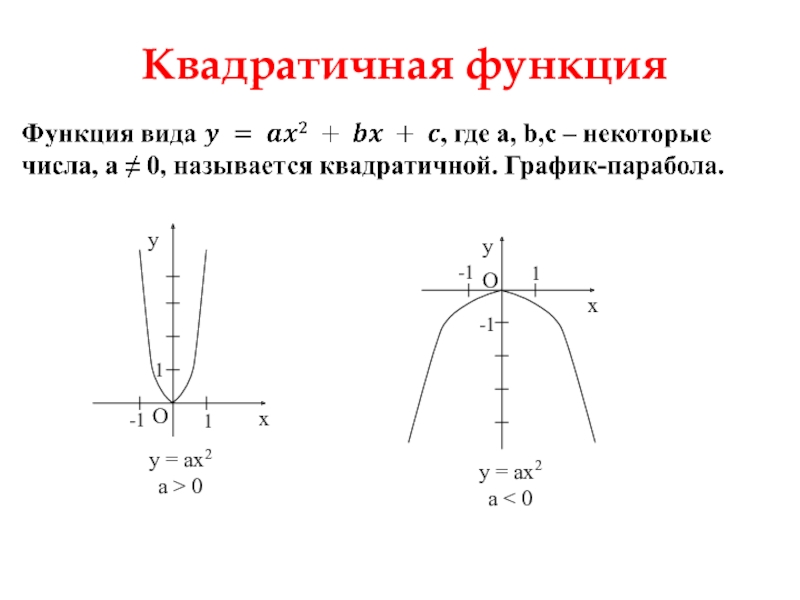
- 6. Квадратичная функция
- 7. аналитический (с помощью формулы);
- 8. График функцииГрафиком функции называется множество всех точек
- 9. Общая схема
- 10. ху0ху0
- 11. y = x³ y = x²-1
- 12. Слайд 12
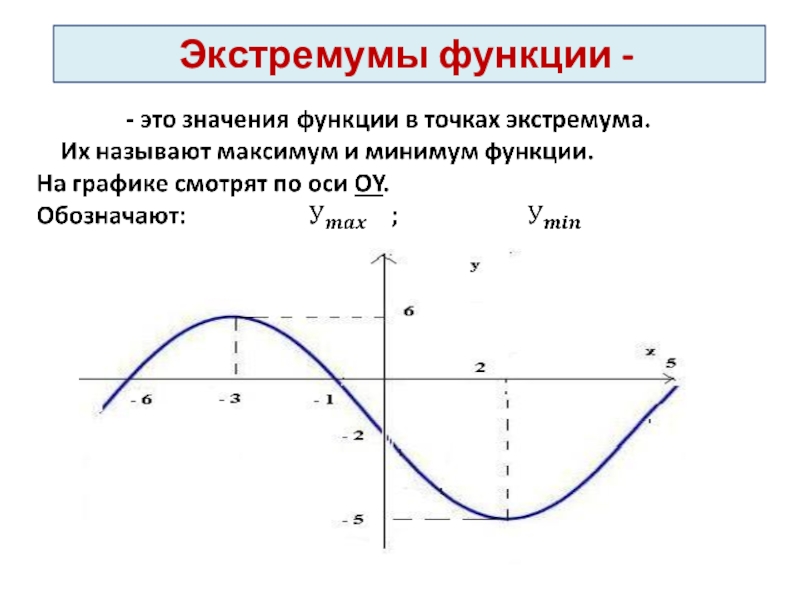
- 13. уmaxуminyx
- 14. Слайд 14
- 15. Слайд 15
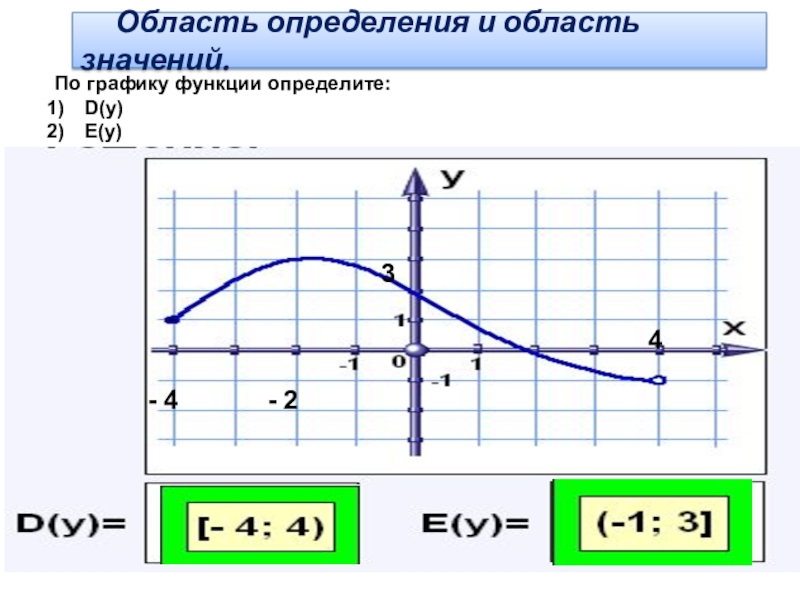
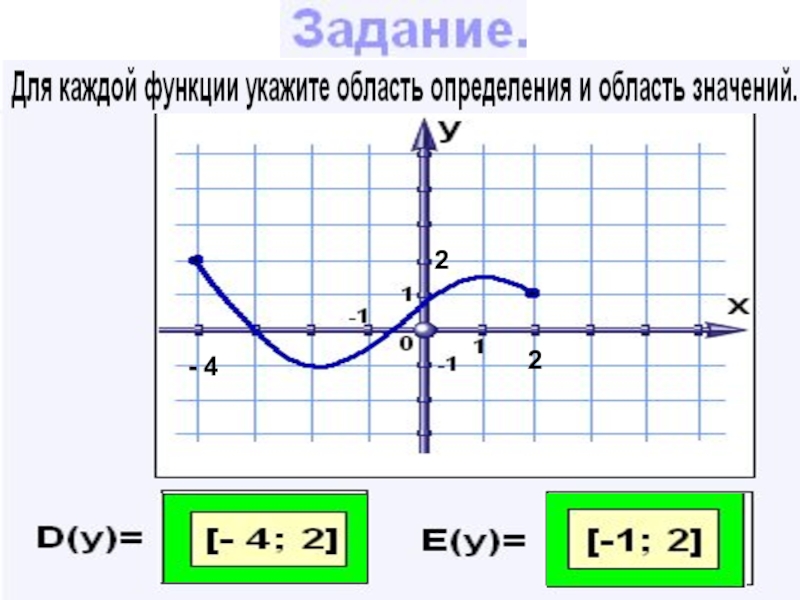
- 16. - 4 4 3По графику функции определите:D(у) Е(у) - 2 Область определения и область значений.
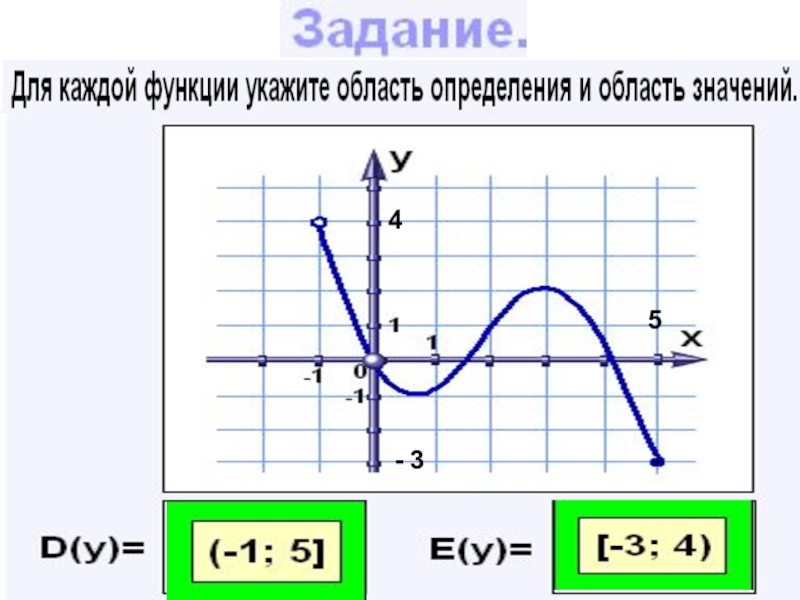
- 17. - 3 5 4
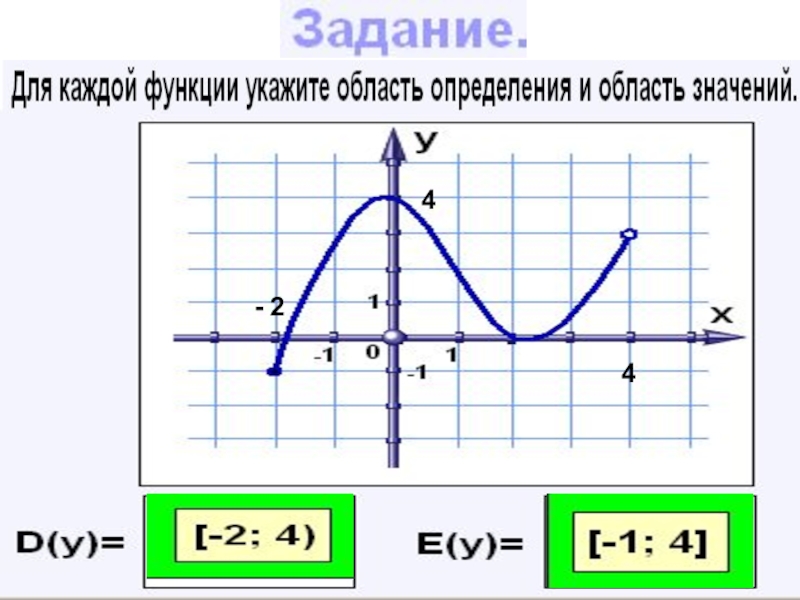
- 18. - 2 4 4
- 19. - 4 2 2
- 20. Задание. Найдите
- 21. Найдите область значений функции:Задание.в) у
- 22. Чётность и нечётностьПримеры
- 23. Примеры нечётных функций: y = x3; y
- 24. При построении графиков чётной и нечётной
- 25. Нули функции-
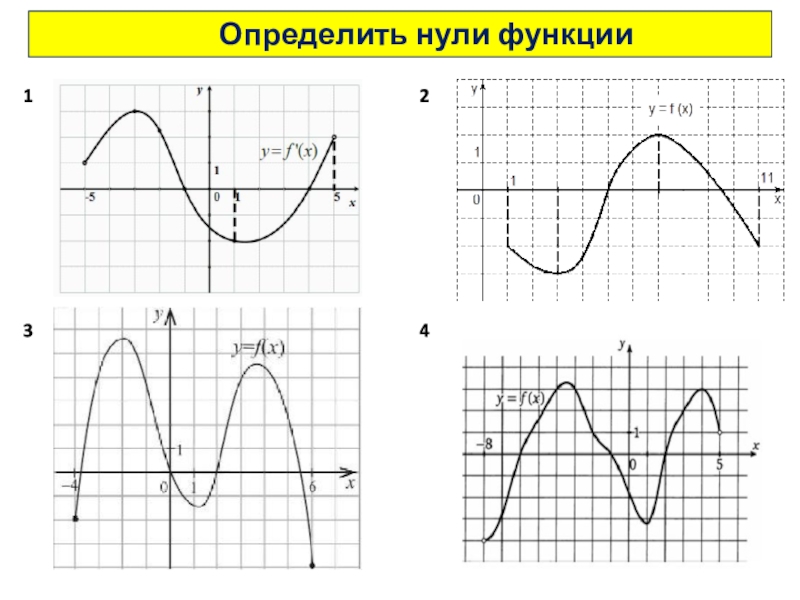
- 26. 1234 Определить нули функции
- 27. Промежутки монотонности--это
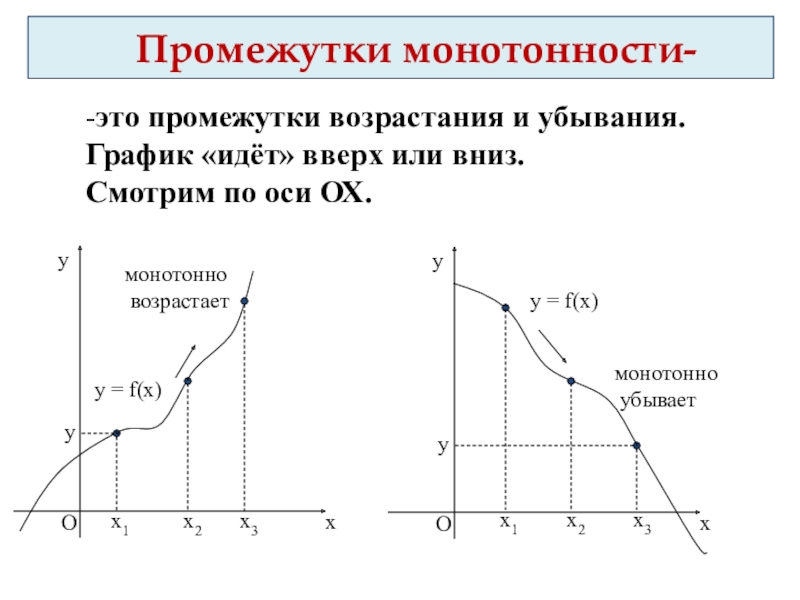
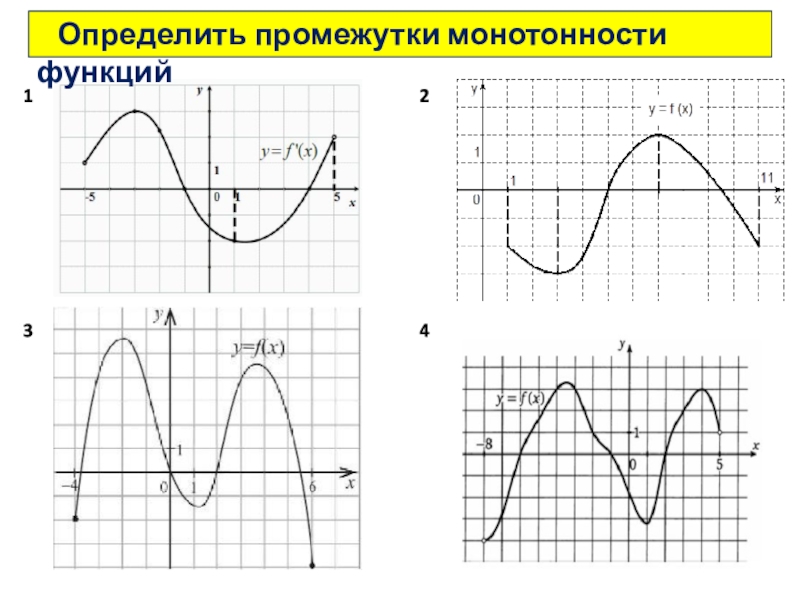
- 28. 1234 Определить промежутки монотонности функций
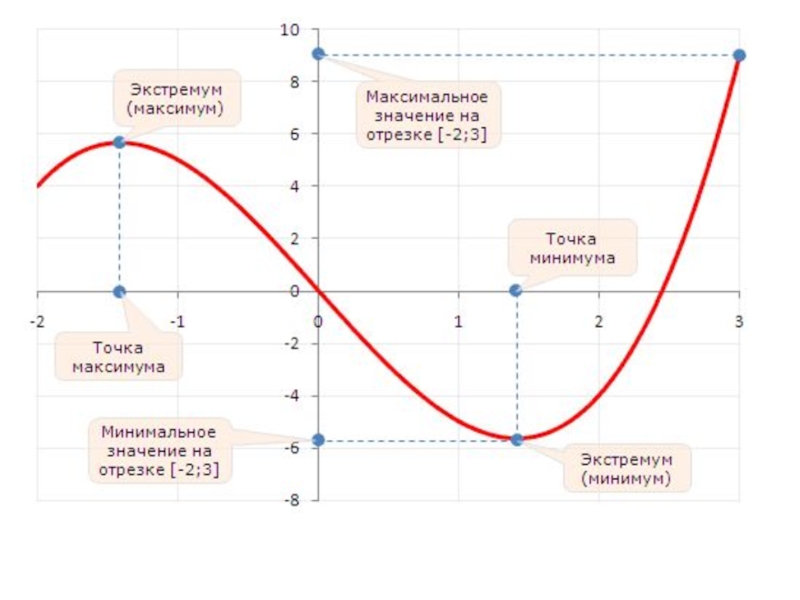
- 29. Точки экстремума функции -
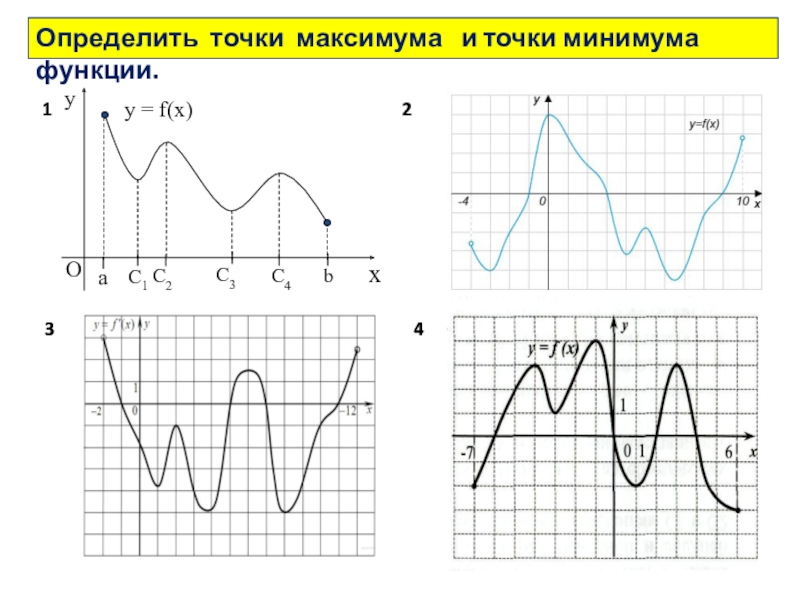
- 30. Определить точки максимума и точки минимума функции. 1234
- 31. Экстремумы функции -
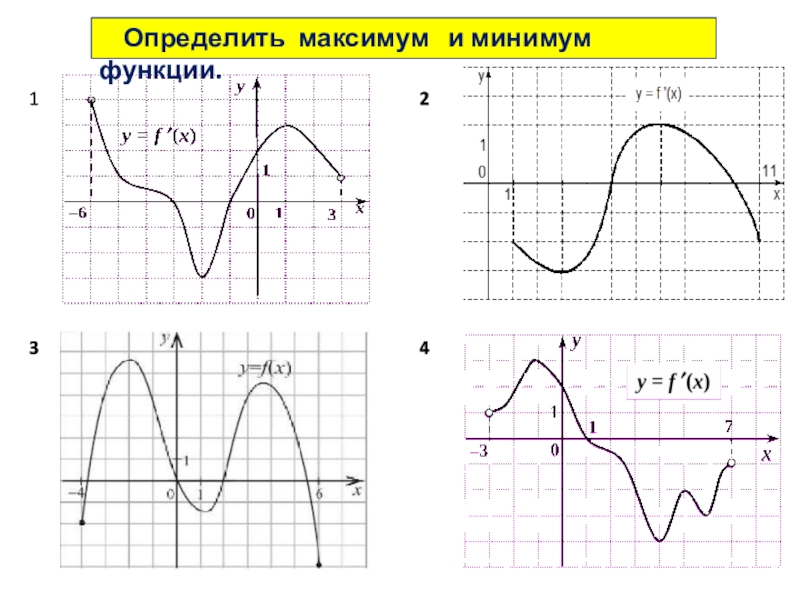
- 32. Определить максимум и минимум функции. 1324
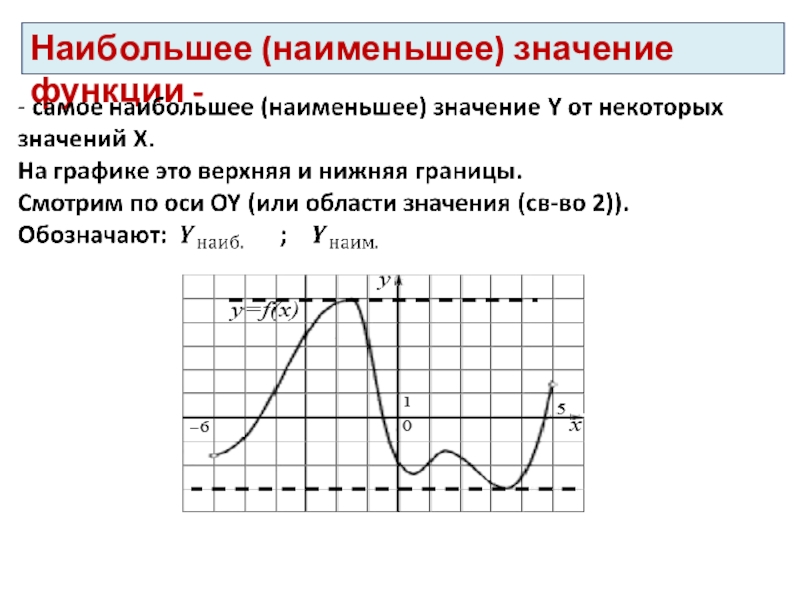
- 33. Наибольшее (наименьшее) значение функции -
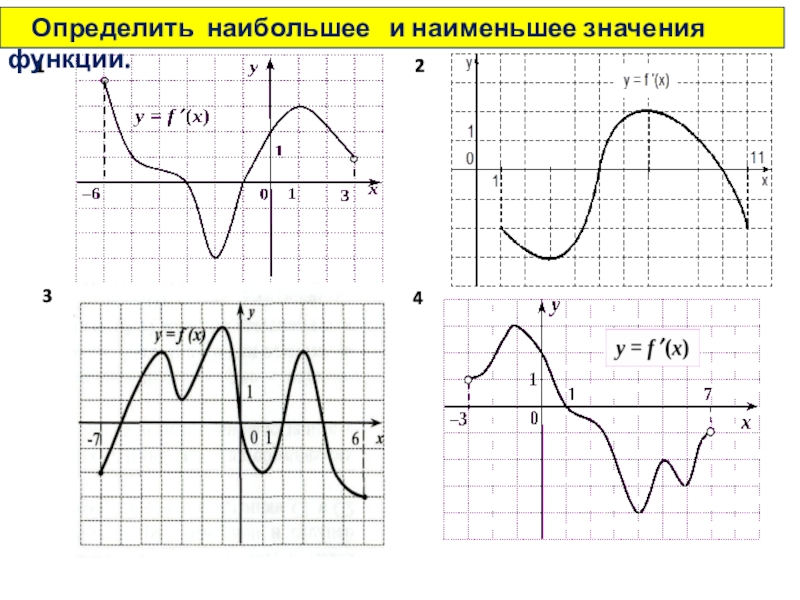
- 34. 1423 Определить наибольшее и наименьшее значения функции.
- 35. Слайд 35
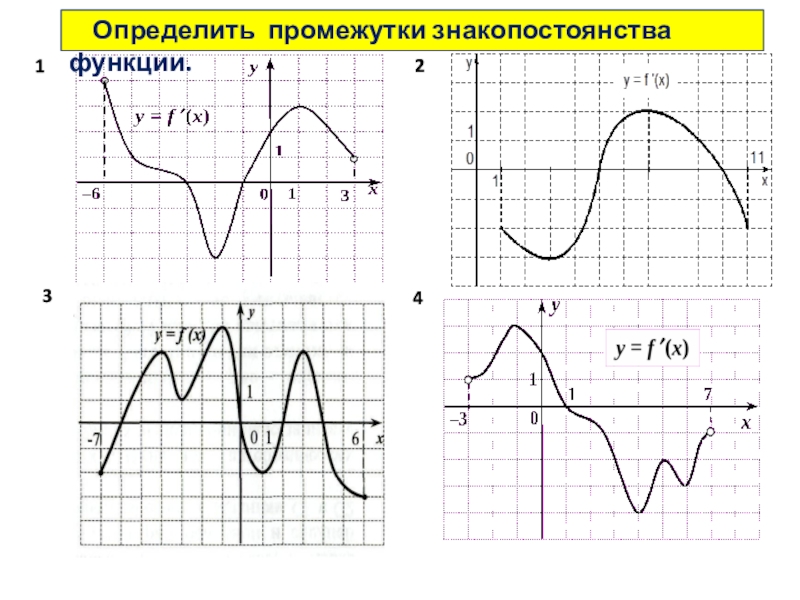
- 36. Промежутки знакопостоянства --это значения аргумента, при которых
- 37. 1423 Определить промежутки знакопостоянства функции.
- 38. Период (от греч. Periodos) – обход, круговращение,
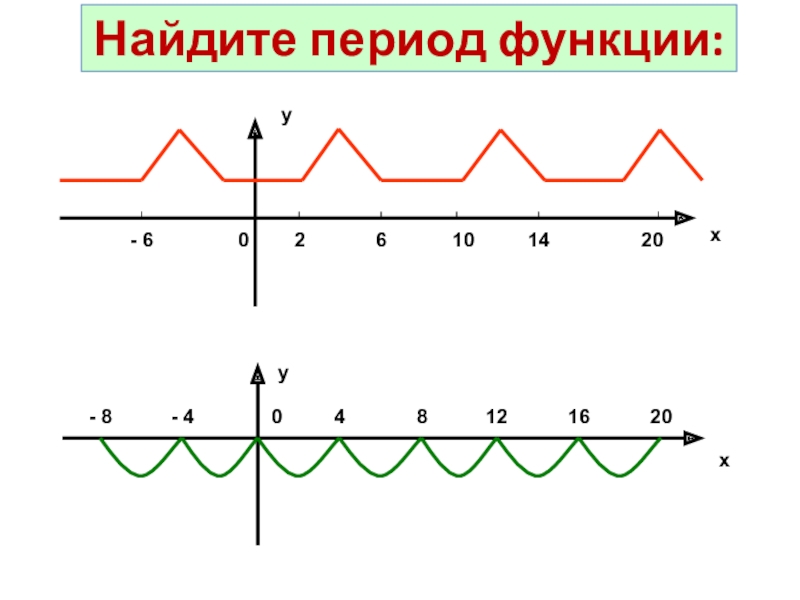
- 39. Найдите период функции:
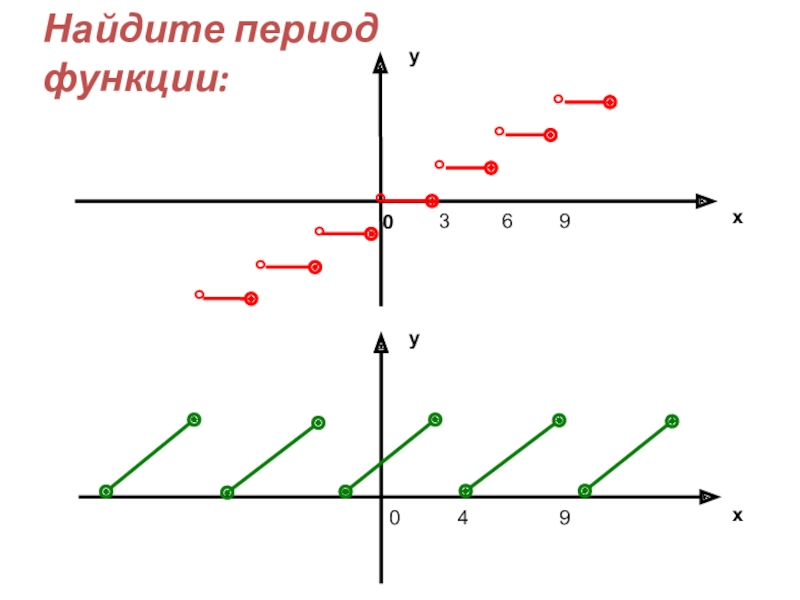
- 40. Найдите период функции:yx0yx049369
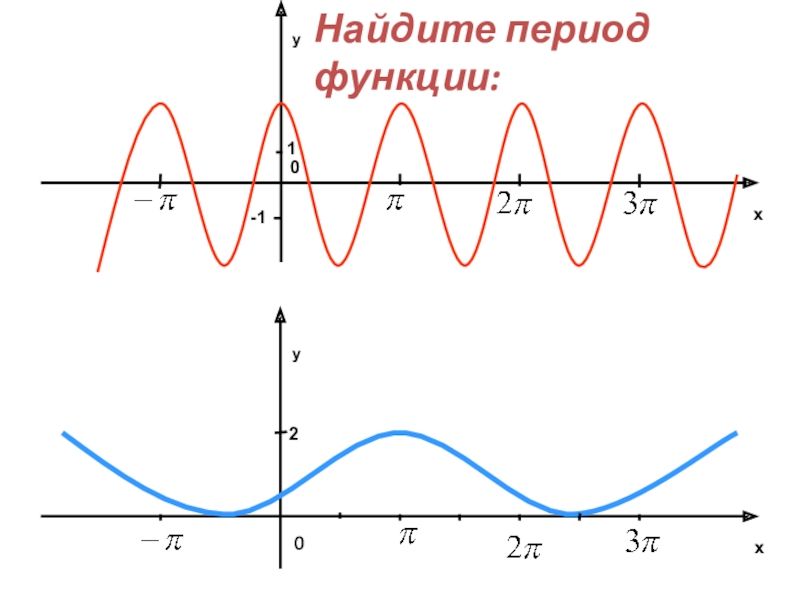
- 41. yx01-1xy02Найдите период функции:
- 42. xy0T/2-T/23T/2-1,5Tyx2,5T0T/2-T/23T/2-TT2T-1,5TДостройте график функции на промежутке [ -1,5 T; 2,5 T].-TT2T2,5TТ = 4Т = 4
- 43. Достройте график функции на промежутке [ -T; 2T]. уухх-Т0Т2Т2ТТ-Т Данная функция является чётной или нечётной?
- 44. Слайд 44
- 45. Слайд 45
Слайд 2 При изучении явлений окружающего мира и в практической деятельности нам
Математика изучает зависимость между величинами в процессе их изменения. Например, при изменении радиуса круга меняется и его площадь, и мы рассматриваем вопрос об изменении площади круга в зависимости от изменения его радиуса.
Математическим выражением взаимной связи реальных величин является идея функциональной зависимости. Понятие функции – важнейшее понятие математики. Слово «функция» (от латинского «Functio» - исполнение обязанностей, деятельность) впервые ввел немецкий ученый Г. Лейбниц.
Введение
Слайд 3Функция-зависимость одной величины от другой, выраженная некоторой формулой(выражением) y=f(x) g(х), f(х) – функция х-независимая
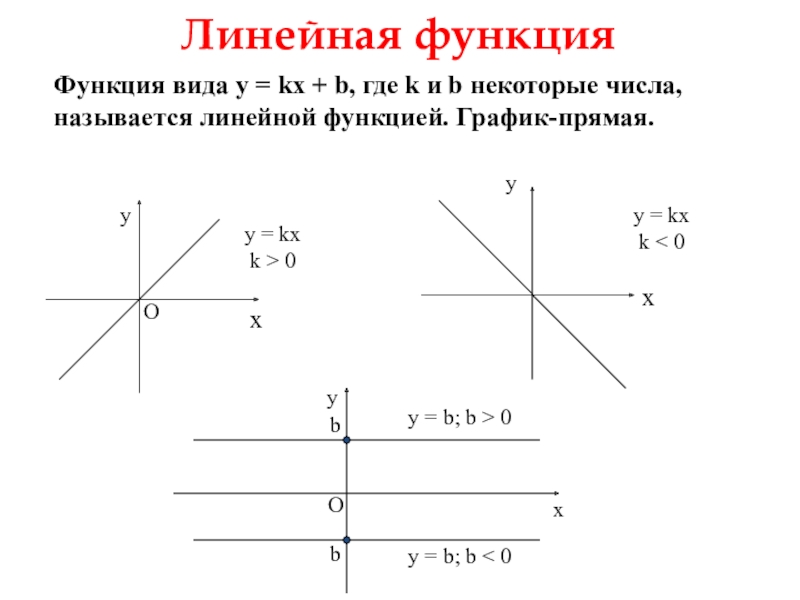
Слайд 4Линейная функция
Функция вида y = kx + b, где k и
y = kx
k < 0
y
x
Слайд 7 аналитический (с помощью формулы);
графический (с помощью
табличный (с помощью таблицы значений);
словесный (правило задания функции описывается словами).
Способы задания функции:
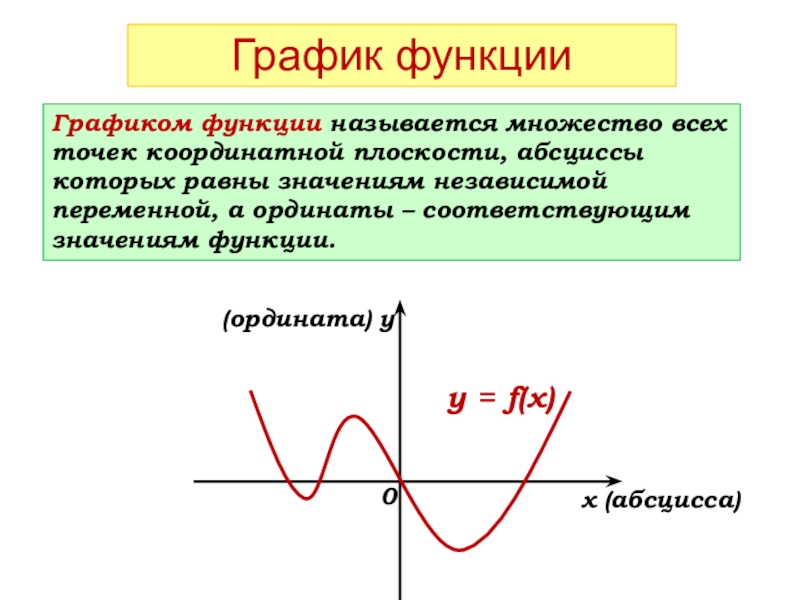
Слайд 8График функции
Графиком функции называется множество всех точек координатной плоскости, абсциссы которых
x (абсцисса)
(ордината) y
y = f(x)
0
Слайд 9 Общая схема исследования функции:
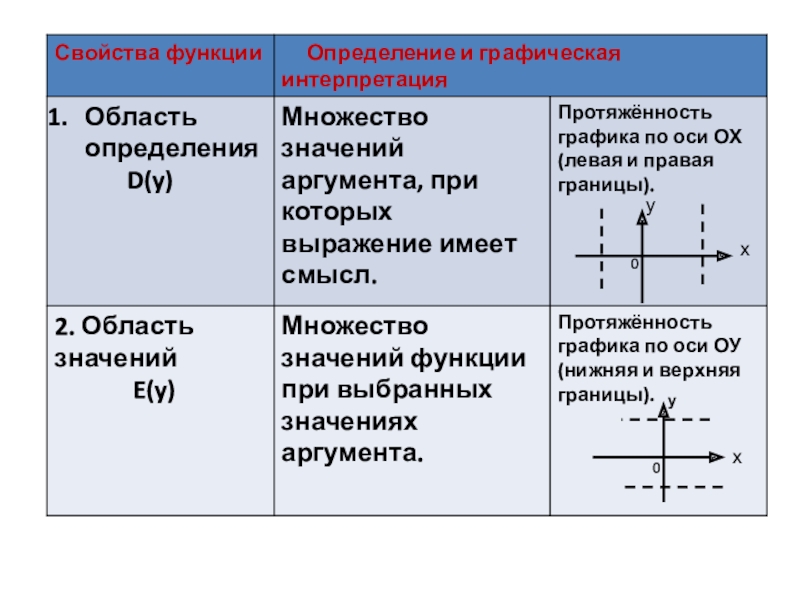
1) D(у)- область
2) Е(у)- область значений
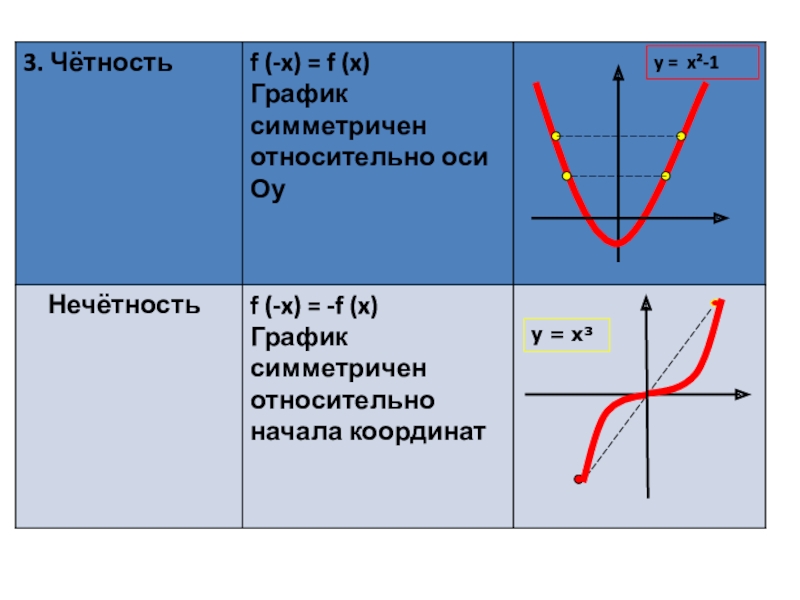
3) Чётность(нечётность) функции
4) Нули функции
5) Промежутки монотонности
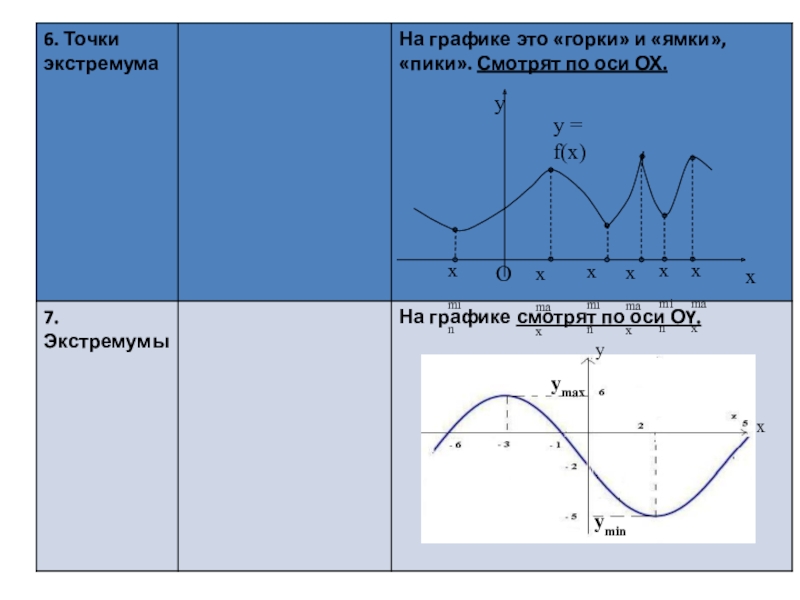
6) Точки экстремумов
7) Экстремумы
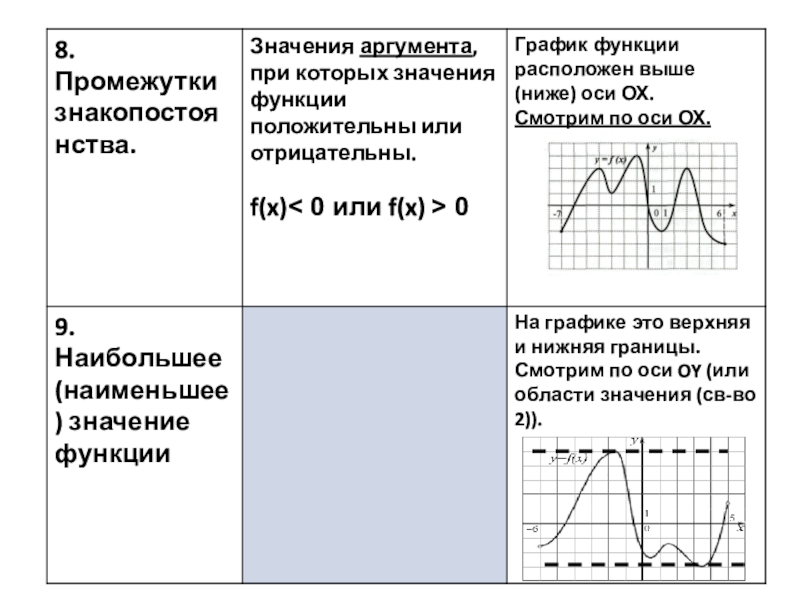
8) Промежутки знакопостоянства
9) Наибольшее (наименьшее) значение функции
10) Периодичность
Слайд 20Задание.
Найдите область значений функции:
-1 ≤ sin x ≤ 1
-1+7 ≤ sin x +7 ≤ 1+7
6 ≤ sin x +7 ≤ 8
Ответ: у Є [6;8]
Слайд 21 Найдите область значений функции:
Задание.
в) у = 4cos x
а)
г) y = -2sin x
б) y = cos x - 1
д) y = 2sin x +3
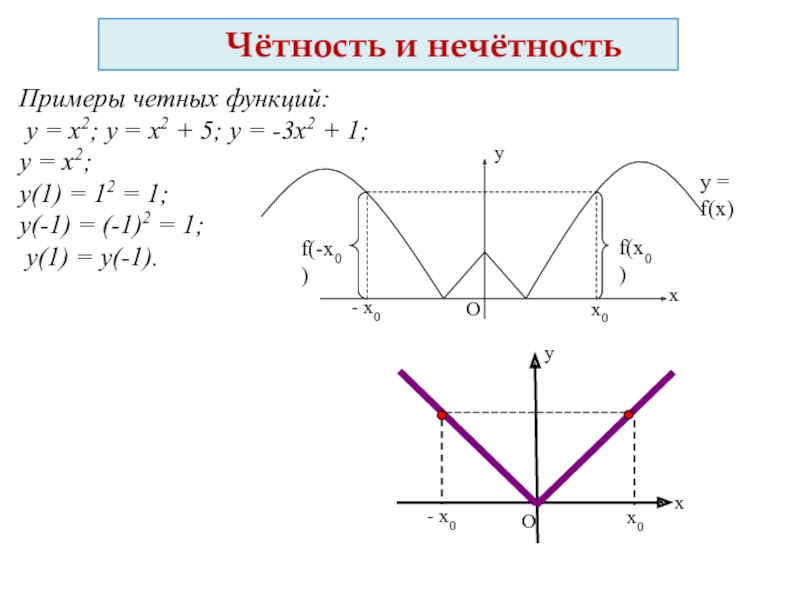
Слайд 22 Чётность и нечётность
Примеры четных функций:
y =
y = x2;
y(1) = 12 = 1;
y(-1) = (-1)2 = 1;
y(1) = y(-1).
y
x
O
x0
- x0
y
x
O
- x0
x0
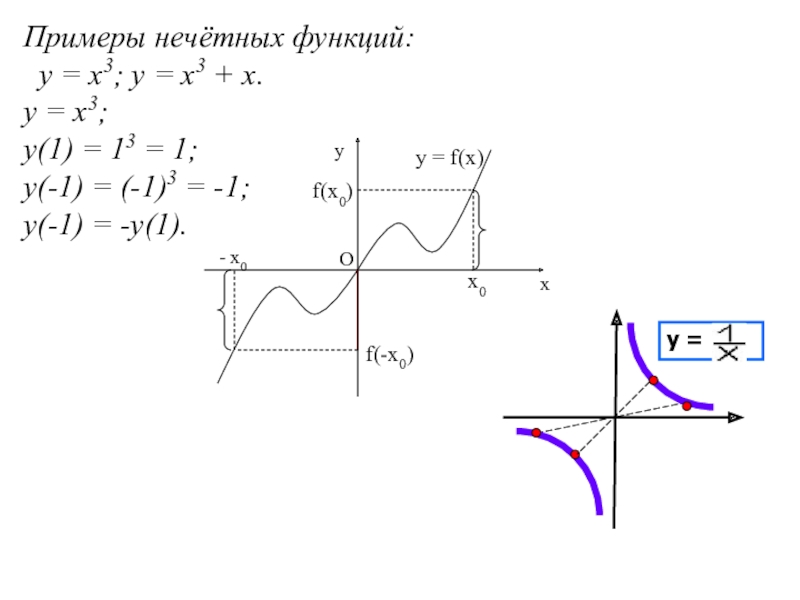
Слайд 23Примеры нечётных функций:
y = x3; y = x3 + x.
y = x3;
y(1) = 13 = 1;
y(-1) = (-1)3 = -1;
y(-1) = -y(1).
f(-x0)
O
y = f(x)
y =
Слайд 24 При построении графиков чётной и нечётной функции достаточно построить только
Конечно, большинство функций не являются ни чётными, ни нечётными.
Пример:
y = x3 + x2
y(-1) = (-1)3 + (-1)2 = -1 + 1 = 0
y(1) = (1)3 + (1)2 = 1 + 1 = 2
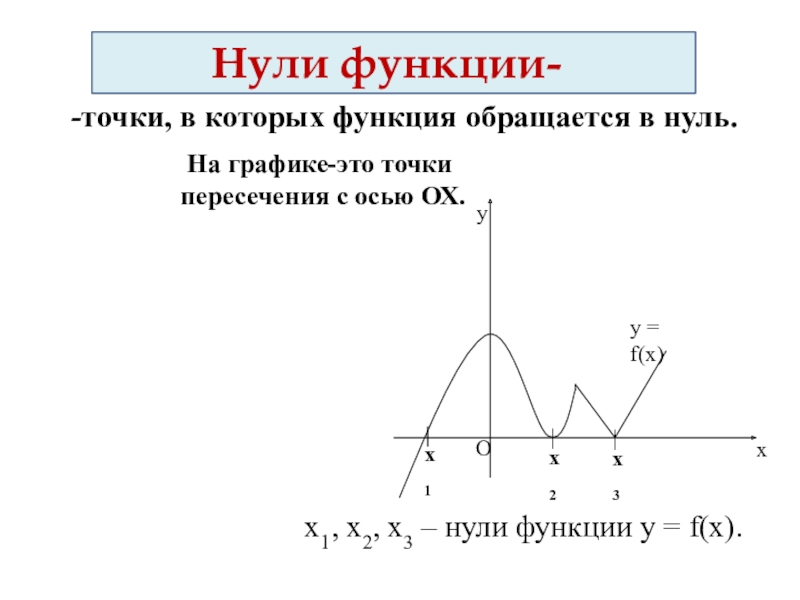
Слайд 25 Нули функции-
-точки, в которых функция
На графике-это точки пересечения с осью ОХ.
х1, х2, х3 – нули функции у = f(x).
Слайд 27 Промежутки монотонности-
-это промежутки возрастания и убывания.
Смотрим по оси ОХ.
y = f(x)
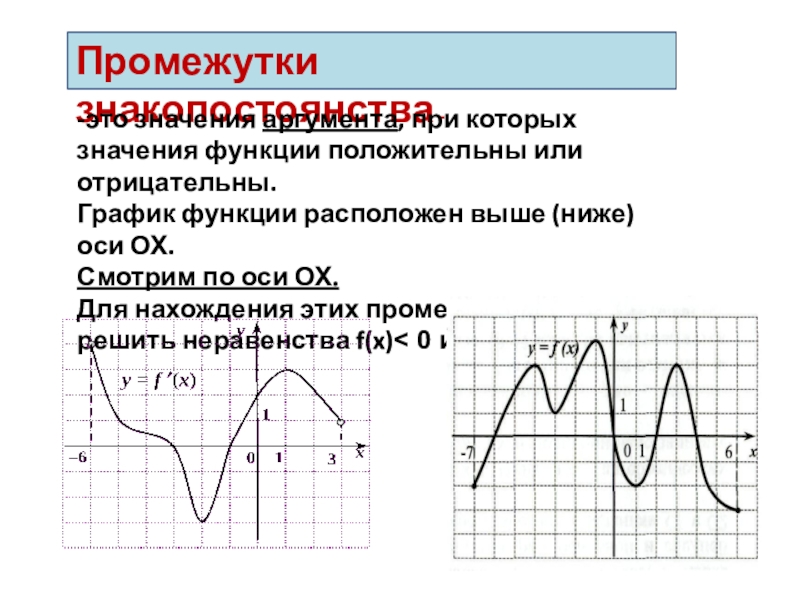
Слайд 36Промежутки знакопостоянства -
-это значения аргумента, при которых значения функции положительны или
График функции расположен выше (ниже) оси ОХ.
Смотрим по оси ОХ.
Для нахождения этих промежутков надо решить неравенства f(x)˂ 0 или f(x) ˃ 0.
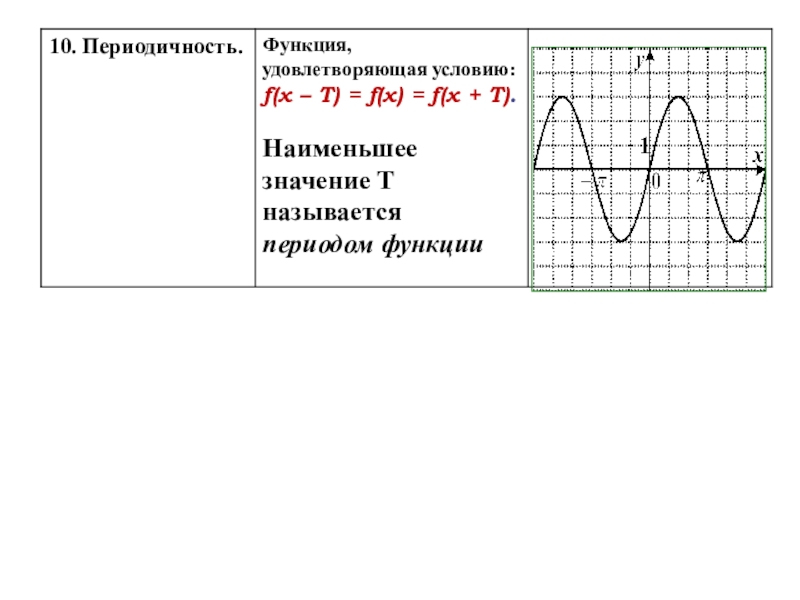
Слайд 38Период (от греч. Periodos) – обход, круговращение, определённый круг времени
T-период
Функцию у=f(x)
f ( x - T) = f(x) = f(x + T) Т - период функции у=f(x)
Слайд 42x
y
0
T/2
-T/2
3T/2
-1,5T
y
x
2,5T
0
T/2
-T/2
3T/2
-T
T
2T
-1,5T
Достройте график функции
на промежутке [ -1,5 T; 2,5 T].
-T
T
2T
2,5T
Т =
Т = 4











![Презентация по математике на тему Функции и их свойства xy0T/2-T/23T/2-1,5Tyx2,5T0T/2-T/23T/2-TT2T-1,5TДостройте график функции на промежутке [ -1,5 T; 2,5 T].-TT2T2,5TТ = 4Т = 4 xy0T/2-T/23T/2-1,5Tyx2,5T0T/2-T/23T/2-TT2T-1,5TДостройте график функции на промежутке [ -1,5 T; 2,5 T].-TT2T2,5TТ = 4Т = 4](/img/thumbs/37c560aa1e3245de2df46d035ffb3c3a-800x.jpg)
![Презентация по математике на тему Функции и их свойства Достройте график функции на промежутке [ -T; 2T]. уухх-Т0Т2Т2ТТ-Т Данная функция является чётной или нечётной? Достройте график функции на промежутке [ -T; 2T]. уухх-Т0Т2Т2ТТ-Т Данная функция является чётной или нечётной?](/img/thumbs/7f9cb90de1be321d7d61a1e877e0b8ba-800x.jpg)







