- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Формула Пика
Содержание
- 1. Презентация по математике на тему Формула Пика
- 2. Объект исследования: задачи на клетчатой бумаге.Предмет исследования:
- 3. Задачи: 1.Изучить источники и отобрать материал
- 4. Гипотеза: Если геометрическая фигура изображена на
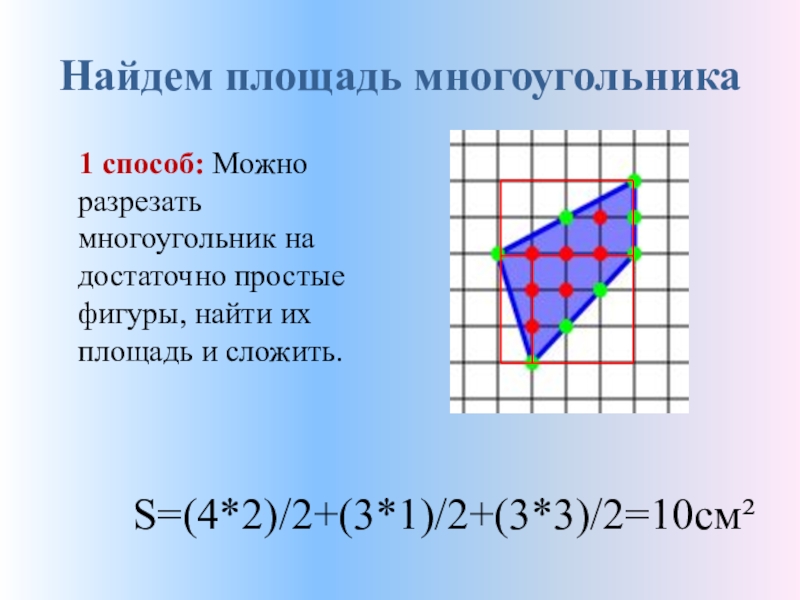
- 5. Найдем площадь многоугольника 1 способ: Можно
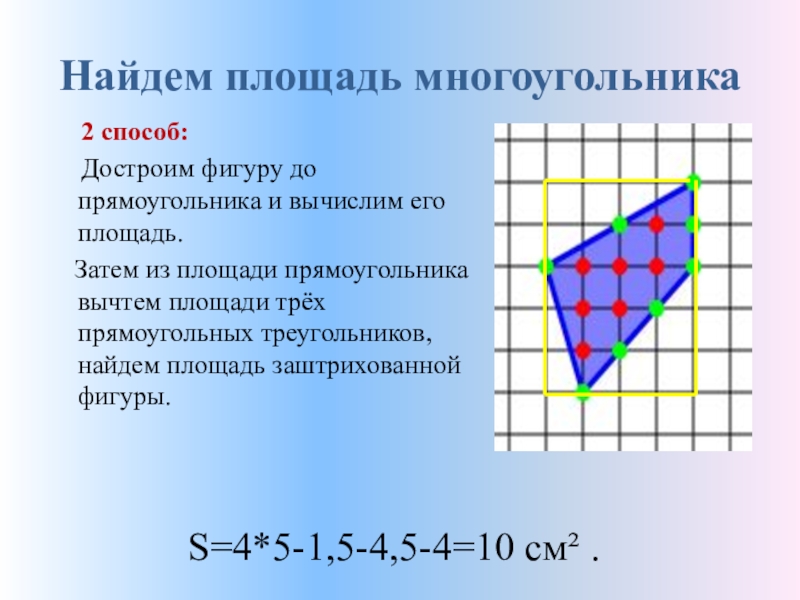
- 6. Найдем площадь многоугольника 2 способ:
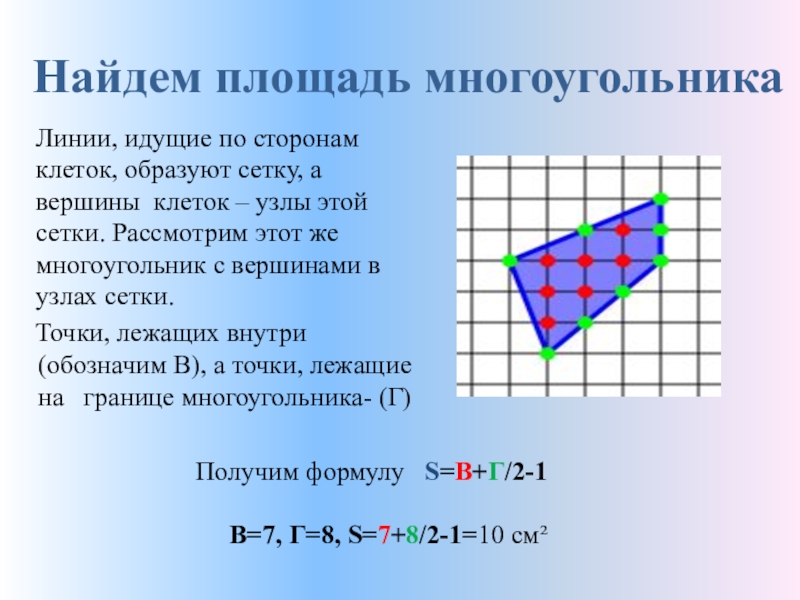
- 7. Найдем площадь многоугольникаЛинии, идущие
- 8. Формула ПикаПик Георг Александров (1859-1943 гг.) –
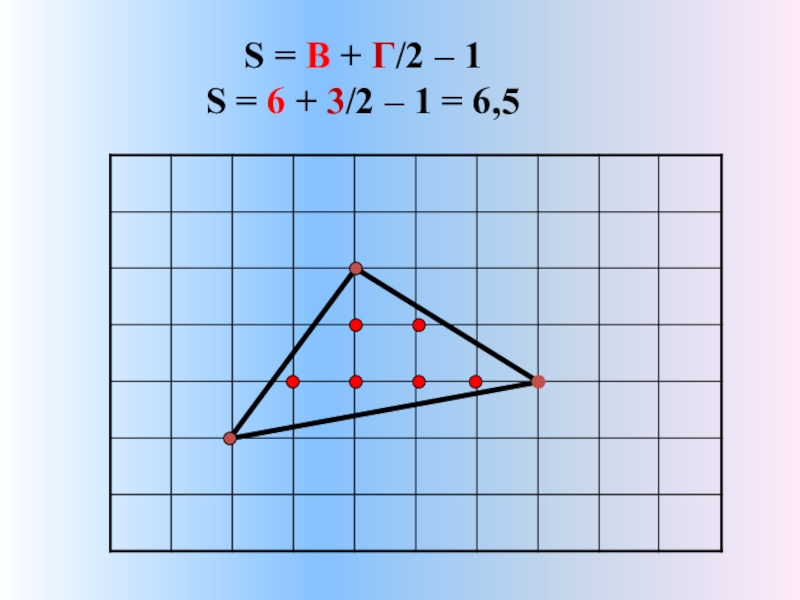
- 9. S = В + Г/2 – 1 S = 6 + 3/2 – 1 = 6,5
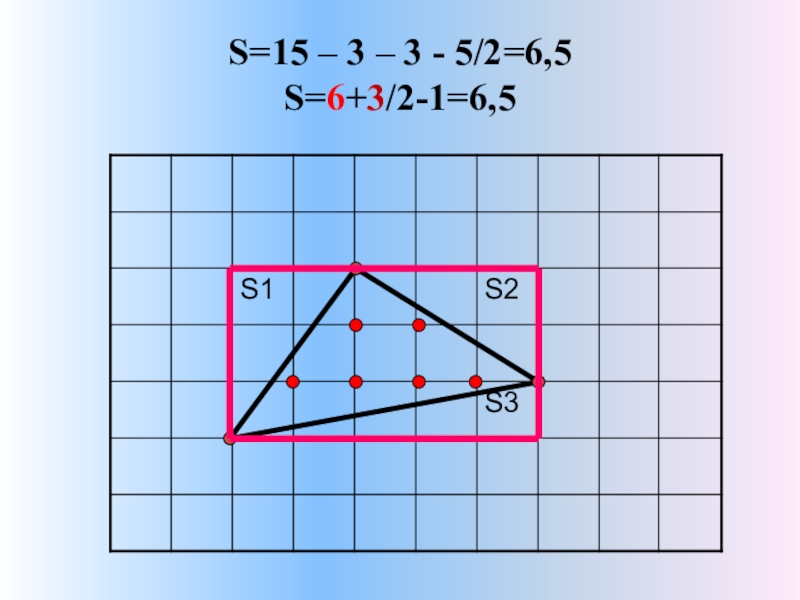
- 10. S=15 – 3 – 3 - 5/2=6,5 S=6+3/2-1=6,5
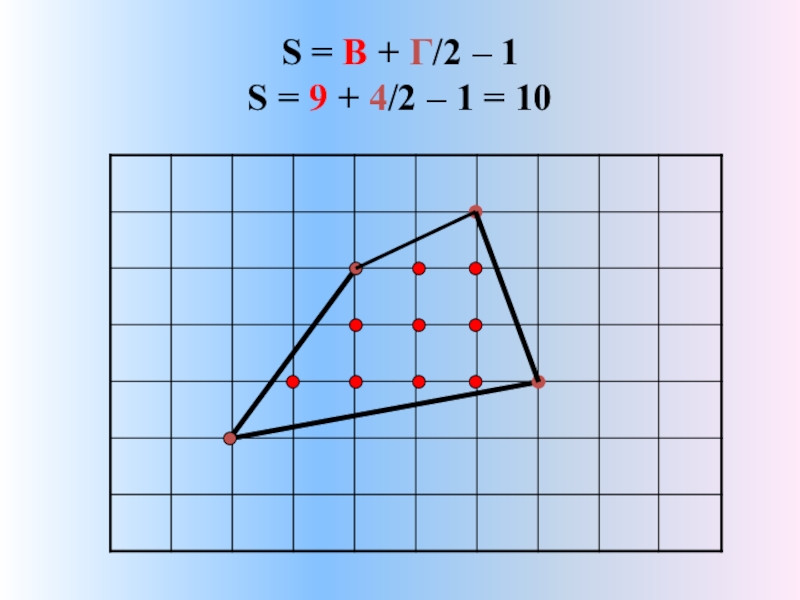
- 11. S = В + Г/2 – 1 S = 9 + 4/2 – 1 = 10
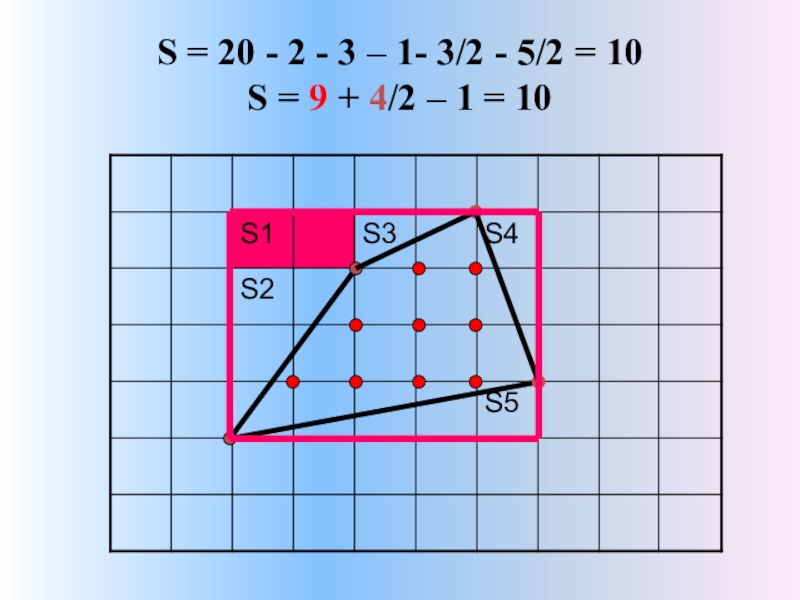
- 12. S = 20 - 2 - 3
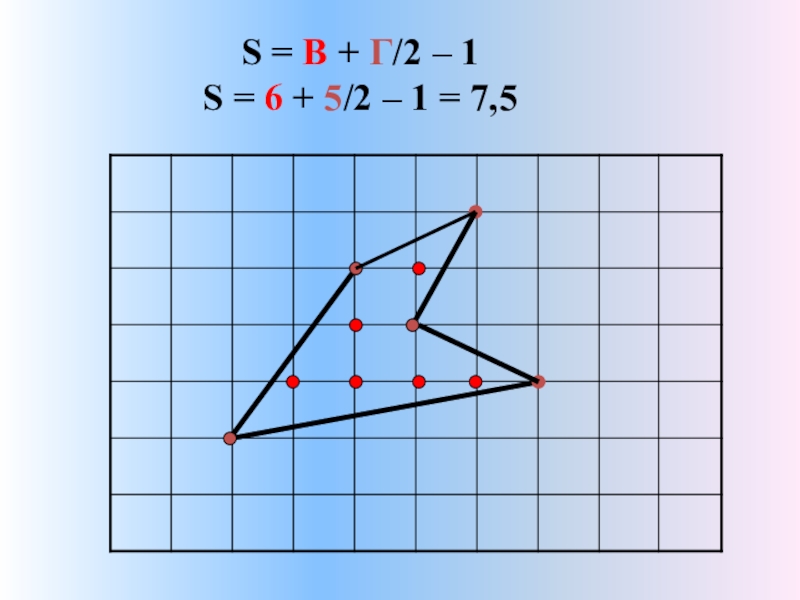
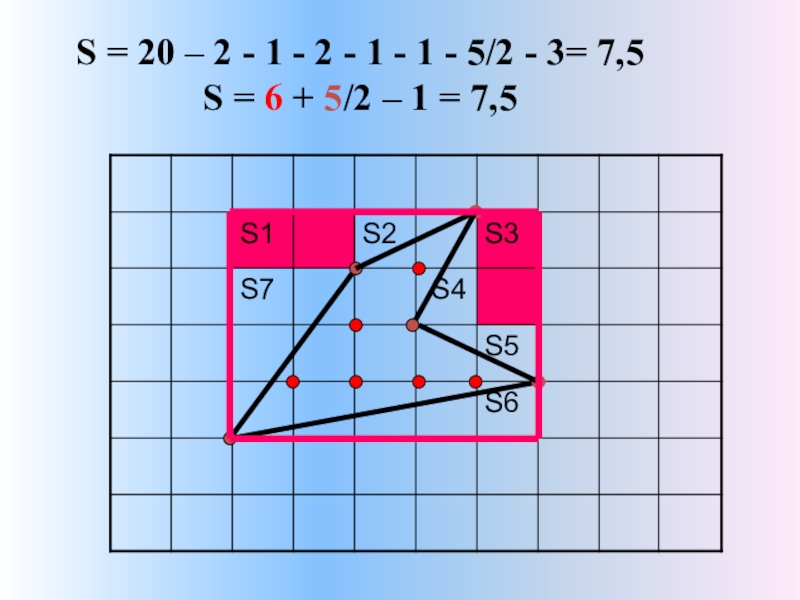
- 13. S = В + Г/2 – 1 S = 6 + 5/2 – 1 = 7,5
- 14. S = 20 – 2 - 1
- 15. В + Г/2 − 1В — есть количество
- 16. Площадь многоугольника с целочисленными вершинами равна В
- 17. Задания ОГЭ и ЕГЭ (2017)Найдите площадь параллелограмма,
- 18. Задания ОГЭ и ЕГЭ (2017)Найдите площадь четырехугольника,
- 19. Вывод:Вычисления по формуле Пика имеет перед другими
- 20. Практическая значимость1.Результаты данного исследования могут быть использованы
- 21. Спасибо за внимание!
Слайд 1Задачи на клетчатой бумаге
Формула Пика
МАОУ «СОШ №74»
г. Пермь
Руководитель: Шляпина Любовь Васильевна
учитель математики
Слайд 2
Объект исследования: задачи на клетчатой бумаге.
Предмет исследования: задачи на вычисление площади
Цель исследования: изучить различные способы решения задач на клетчатой бумаге и познакомиться с формулой Пика.
Слайд 3Задачи:
1.Изучить источники и отобрать материал для исследования.
2. Решить
3. Решить задачи на нахождение площадей фигур, изображённых на клетчатой бумаге с применением формулы Пика.
4.Сравнить и проанализировать результаты исследования.
5.Подобрать задачи на нахождение площадей фигур на клетчатой бумаге.
Слайд 4Гипотеза:
Если геометрическая фигура изображена на клетчатой бумаге, то её
Слайд 5Найдем площадь многоугольника
1 способ: Можно разрезать многоугольник на достаточно
S=(4*2)/2+(3*1)/2+(3*3)/2=10см²
Слайд 6Найдем площадь многоугольника
2 способ:
Достроим фигуру
Затем из площади прямоугольника вычтем площади трёх прямоугольных треугольников, найдем площадь заштрихованной фигуры.
S=4*5-1,5-4,5-4=10 см² .
Слайд 7
Найдем площадь многоугольника
Линии, идущие по сторонам клеток, образуют
Точки, лежащих внутри (обозначим В), а точки, лежащие на границе многоугольника- (Г)
Получим формулу S=B+Г/2-1
В=7, Г=8, S=7+8/2-1=10 см²
Слайд 8Формула Пика
Пик Георг Александров (1859-1943 гг.) – австрийский математик. Открыл формулу
в 1899 году.
S=B+Г/2-1
где В — количество целочисленных точек внутри многоугольника, а Г — количество целочисленных точек на границе многоугольника.
Слайд 15
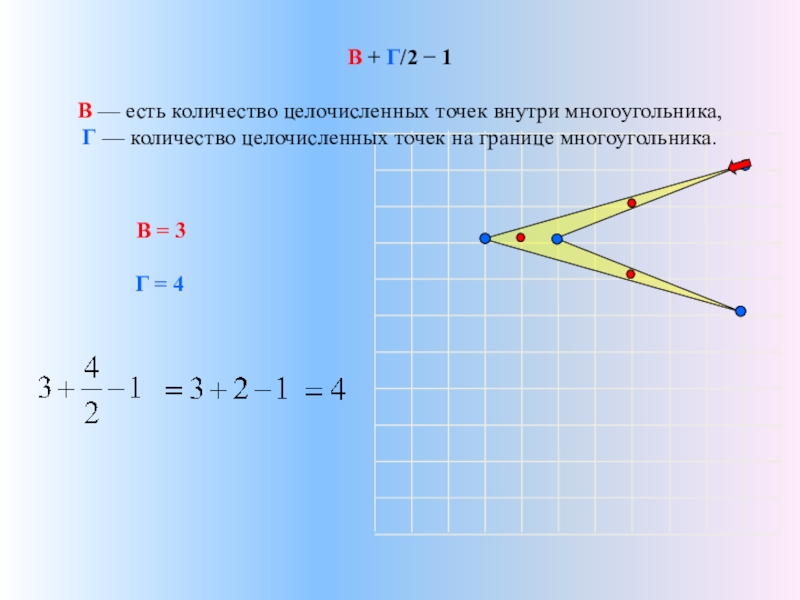
В + Г/2 − 1
В — есть количество целочисленных точек внутри многоугольника,
В = 3
Г = 4
Слайд 16
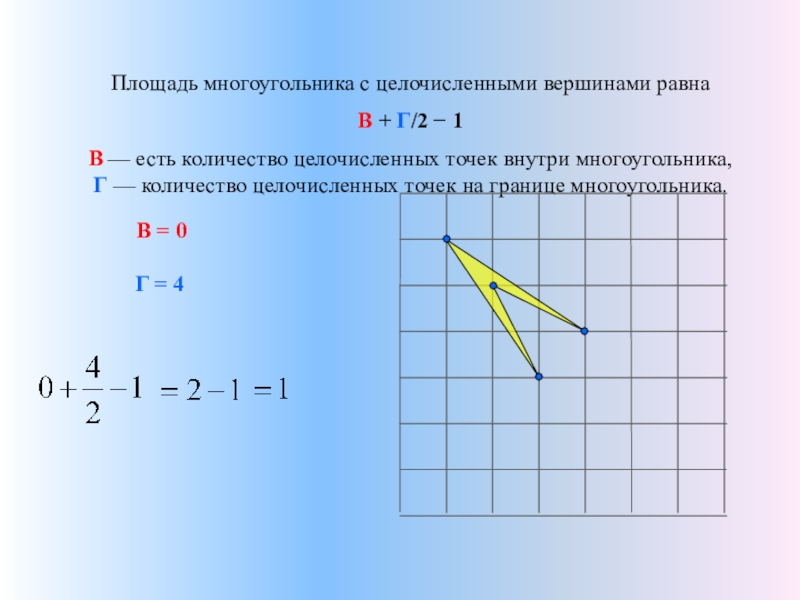
Площадь многоугольника с целочисленными вершинами равна
В + Г/2 − 1
В —
В = 0
Г = 4
Слайд 17Задания ОГЭ и ЕГЭ (2017)
Найдите площадь параллелограмма, изображенного на клетчатой бумаге
Решение.
1способ: Площадь параллелограмма равна произведению основания на высоту, проведенную к этому основанию или его продолжению.
Поэтому S= 4*3 = 12(см²)
2 способ: Приведем другое решение. Площадь параллелограмма равна разности площади прямоугольника и двух равных прямоугольных треугольников, гипотенузы которых являются сторонами параллелограмма.
Поэтому S= 8*4-2*1/2*5*4=12 (см²)
3 способ: По формуле Пика: В=8, Г=10, S=8+5-1 =12(см²)
Слайд 18Задания ОГЭ и ЕГЭ (2017)
Найдите площадь четырехугольника, изображенного на клетчатой бумаге
1способ:
Площадь четырёхугольника равна разности площади трапеции, маленького прямоугольника и двух прямоугольных треугольников, гипотенузы которых являются сторонами исходного четырёхугольника.
Поэтому S=1/2 *(3+2)*3 -1/2*1*2 – 1/2 *1*1- 1*2= 4 (см²)
2 способ:
По формуле Пика: В=2, Г=6, S= В+Г/2 -1=2+3-1=4 (см²)
3 способ: Данный четырёхугольник можно разбить на прямоугольный треугольник, с катетами 1 и 3, прямоугольную трапецию с основаниями 3 и 1 и прямоугольный треугольник с катетами 1 и 1. Поэтому его площадь равна 4 (см²).
Слайд 19Вывод:
Вычисления по формуле Пика имеет перед другими способами ряд преимуществ. Формула
Сравнив результаты, пришли к выводу, что площадь фигуры, вычисленная по формуле Пика, равна площади фигуры, вычисленной по формулам геометрии. Итак, гипотеза оказалась верной.
Слайд 20Практическая значимость
1.Результаты данного исследования могут быть использованы в последующих работах по
2.Материалы работы будут полезны при подготовке к экзамену по математике;
3. Работа по данной теме позволила преодолеть психологический барьер, поверить в свои силы и реализовать свои интеллектуальные возможности.