- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Элементы комбинаторики(1 курс)
Содержание
- 1. Презентация по математике на тему Элементы комбинаторики(1 курс)
- 2. СодержаниеЦели урока.Дерево возможностей.Немного истории.Виды соединений, определение факториала.Перестановки.Размещения.Сочетания.Существенные признаки соединений.Различия и сходства соединений.Решение задач.Используемая литература
- 3. Цели урока: Образовательныевыявить, обобщить и расширить математические
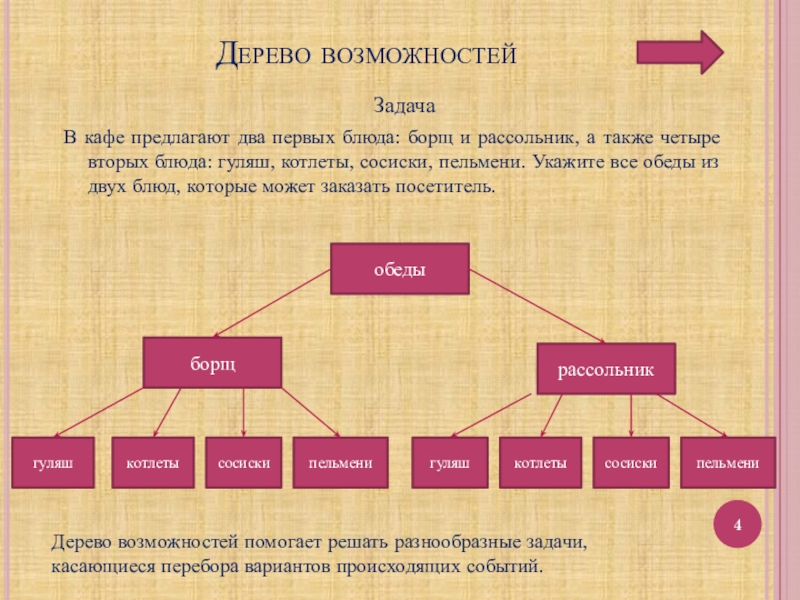
- 4. Дерево возможностей ЗадачаВ кафе предлагают два
- 5. Немного историиКомбинаторика – ветвь математики , изучающая
- 6. В частности, одним из видов комбинаторных задач
- 7. 25.09.2010Кошехабльский районПерестановки.Опр. Перестановкой из n элементов называется
- 8. 25.09.2010Кошехабльский районРазмещенияОпр. Размещением из n элементов по
- 9. 25.09.2010Кошехабльский районСочетанияОпр. Сочетанием из n элементов по
- 10. 25.09.2010Кошехабльский район
- 11. 25.09.2010Кошехабльский районПерестановки Размещения Сочетания Размещения Сходства -
- 12. 25.09.2010Кошехабльский районРешение задачПять мальчиков и четыре девочки
- 13. 25.09.2010Кошехабльский район Что мы сегодня усвоили на
Слайд 2Содержание
Цели урока.
Дерево возможностей.
Немного истории.
Виды соединений, определение факториала.
Перестановки.
Размещения.
Сочетания.
Существенные признаки соединений.
Различия и сходства
Решение задач.
Используемая литература
Слайд 3Цели урока:
Образовательные
выявить, обобщить и расширить математические знания в области комбинаторики
ввести
формирование умений по применению знаний в решении задач
Воспитательные
воспитывать усидчивость, инициативность
Развивающие
развивать логическое мышление, внимательность,память
Развивать умение рассуждать, обобщать, делать выводы
Слайд 4Дерево возможностей
Задача
В кафе предлагают два первых блюда: борщ и
борщ
гуляш
обеды
рассольник
котлеты
сосиски
пельмени
гуляш
котлеты
сосиски
пельмени
Дерево возможностей помогает решать разнообразные задачи,
касающиеся перебора вариантов происходящих событий.
Слайд 5Немного истории
Комбинаторика – ветвь математики , изучающая комбинации перестановки предметов .Еще
Комбинаторика возникла в 17 веке. Комбинаторные навыки оказались полезными в часы досуга. В таких играх как нарды, карты, шашки, шахматы приходилось рассматривать различные сочетания фигур и выигрывал тот, кто их лучше изучил, знал выигрышные комбинации и умел избегать проигрышные.
Еще с давних пор дипломаты стремясь к тайне переписке, изобретали сложные шифры, а секретные службы пытались эти шифры разгадать.
Методы комбинаторики находят широкое применение в физике, химии, биологии, экономике и др. областях.
В науке и практике часто встречаются задачи, решая которые приходится составлять различные комбинации из конечного числа элементов и подсчитывать число комбинаций. Такие задачи получили название комбинаторных задач.
Слайд 6В частности, одним из видов комбинаторных задач являются
задачи на соединения
Виды
размещения
сочетания
перестановки
В задачах по комбинаторике часто применяется такое понятие как
факториал ( в переводе с английского « factor» – множитель)
n! = 1· 2· 3· …· (n -1)n
Слайд 725.09.2010
Кошехабльский район
Перестановки.
Опр. Перестановкой из n элементов называется последовательность,
причем число элементов этой последовательности равно n.
Формула (число размещений «из эн по эм»):
Задача: В расписании сессии 3 экзамена (история, геометрия, алгебра). Сколько может быть вариантов расписаний?
Решение. (обратить внимание на его оформление!)
Основное множество: {история, геометрия, алгебра}
Соединение – вариант расписания сессии
Проверим, важен ли порядок:
{история, геометрия, алгебра} и {геометрия, история, алгебра} – варианты расписания сессии для разных групп порядок важен это последовательность это перестановка из трех элементов.
Ответ: 6 вариантов
Слайд 825.09.2010
Кошехабльский район
Размещения
Опр. Размещением из n элементов по m ( m ≤
Формула (число размещений «из эн по эм»):
Решение (обратить внимание на его оформление!)
Основное множество: {1, 3, 5, 7, 9} – нечетные цифры
Соединение – двузначное число
Задача: Сколько существует двузначных чисел, в которых цифра десятков и цифра единиц различны и нечетны?
Проверим, важен ли порядок:
разные двузначные числа
порядок важен это последовательность это размещение «из пяти по два».
двузначных чисел
Ответ: 20 чисел.
Слайд 925.09.2010
Кошехабльский район
Сочетания
Опр. Сочетанием из n элементов по m ( m ≤
Формула (число размещений «из эн по эм»):
Задача: Сколькими способами можно составить букет из 3 цветов, если в вашем распоряжении 5 цветов: мак, роза, тюльпан, лилия, гвоздика?
Решение. (обратить внимание на его оформление!)
Основное множество: {мак, роза, тюльпан, лилия, гвоздика}
Соединение – букет из трех цветков
Проверим, важен ли порядок:
{тюльпан, лилия, гвоздика} и {лилия, тюльпан, гвоздика} – один и тот же букет порядок неважен это подмножество это сочетание «из пяти по три».
Ответ: 10 букетов
Слайд 1125.09.2010
Кошехабльский район
Перестановки
Размещения
Сочетания
Размещения
Сходства - это последовательности элементов n-
подмножества. В них имеет значение порядок следования
элементов последовательности.
Различия - в размещении могут участвовать не все элементы
исходного множества. В перестановке участвуют все
элементы исходного множества.
Различия - сочетание – это подмножество, содержащее m элементов
из n. Размещение – это последовательность,
содержащая m элементов из n.
При формировании последовательности важен порядок следования
Элементов, а при формировании подмножества порядок не важен.
Слайд 1225.09.2010
Кошехабльский район
Решение задач
Пять мальчиков и четыре девочки хотят сесть на девятиместную
В библиотеке читателю предложили на выбор из новых поступлений 10 книг и 4 журнала. Сколькими способами он может выбрать из них 3 книги и 2 журнала?
Сколько существует семизначных телефонных номеров, в которых все цифры различные и первая цифра отлична от нуля?
Сколько различных трехзначных чисел (без повторения цифр) можно составить из цифр 1, 2, 3, 4, 5, таких, которые являются: а) четными; б) кратными 5 ?
Слайд 1325.09.2010
Кошехабльский район
Что мы сегодня усвоили на уроке?
Что такое комбинаторика?
Запишите формулу.
Что называют сочетанием ?
Запишите формулу.
Что называют перестановкой?
Запишите формулу.
В чем различие между перестановками,
размещениями, сочетаниями?