- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Решение неравенств методом интервалов
Содержание
- 1. Решение неравенств методом интервалов
- 2. План применения метода интервалов!
- 3. №1. Решите методом интервалов неравенства: б) №2.
- 4. Проверь своё решение№1. Решите методом интервалов неравенства:Вариант
- 5. Проверь своё решениеВариант 1.Вариант 2.№2. Найдите область определения функции:60 – – +Ответ:70 – – +Ответ:Решение.Решение.
- 6. Оценка самостоятельной работыЗа каждый верно выполненный пример
- 7. Решим неравенство1) Данный многочлен имеет корни:
- 8. Решите неравенство1 вариант:2 вариант:Сделайте выводы о смене знака на интервалах, в зависимости от степени кратности корня.
- 9. Обобщая ваши наблюдения, делаем выводы:
- 10. Решение рациональных неравенств Итак:
- 11. – Решим неравенство1) Найдем область определения неравенства:откуда2)
Слайд 3
№1. Решите методом интервалов неравенства:
б)
№2. Найдите область определения функции:
Вариант
а)
Вариант 2.
б)
а)
Самостоятельная работа
!
Желаю удачи!
Слайд 4
Проверь своё решение
№1. Решите методом интервалов неравенства:
Вариант 1.
Вариант 2.
а)
а)
2,5
0,4
-3
-4
Ответ:
Ответ:
+
+
–
+
+
б)
б)
1/2
-3/2
+
+
–
Ответ:
1/3
-2/3
+
+
–
Ответ:
Слайд 5
Проверь своё решение
Вариант 1.
Вариант 2.
№2. Найдите область определения функции:
6
0
–
+
Ответ:
7
0
–
–
+
Ответ:
Решение.
Решение.
Слайд 6
Оценка самостоятельной работы
За каждый верно выполненный пример – поставьте 1 балл.
1
2 балла – хорошо, «4».
3 балла – отлично, «5».
0 баллов – плохо, «2».
!
Слайд 7
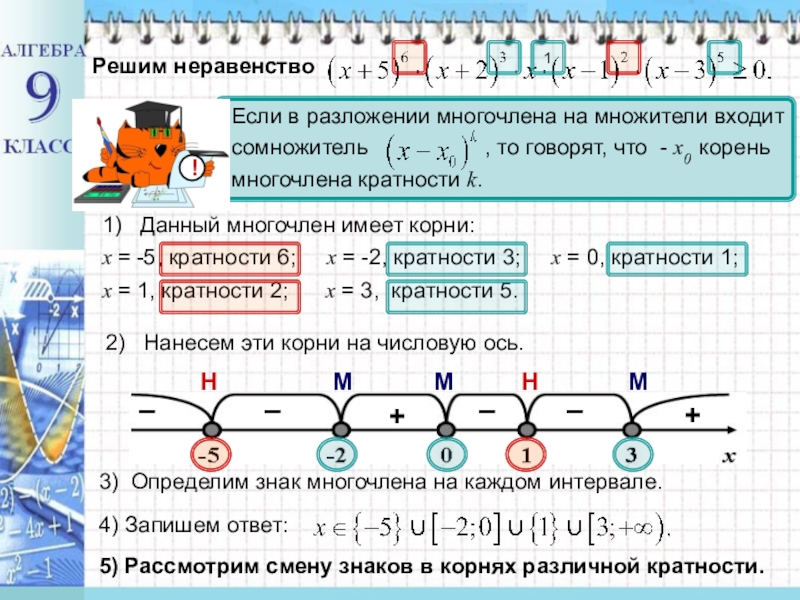
Решим неравенство
1) Данный многочлен имеет корни:
x = -5, кратности
x = 1, кратности 2; x = 3, кратности 5.
2) Нанесем эти корни на числовую ось.
3) Определим знак многочлена на каждом интервале.
+
+
–
–
–
–
4) Запишем ответ:
5) Рассмотрим смену знаков в корнях различной кратности.
М
Н
Н
М
М
Слайд 8
Решите неравенство
1 вариант:
2 вариант:
Сделайте выводы о смене знака на интервалах, в
Слайд 11
–
Решим неравенство
1) Найдем область определения неравенства:
откуда
2) Сведем данное рациональное неравенство
3) Находим корни многочлена и определяем их кратность:
х =1 (четная кратность), корни 3, -1, 0, 5, -2 (нечетная кратность).
4) Определим знак многочлена при х = 10, и расставим остальные знаки с учетом кратности корней.