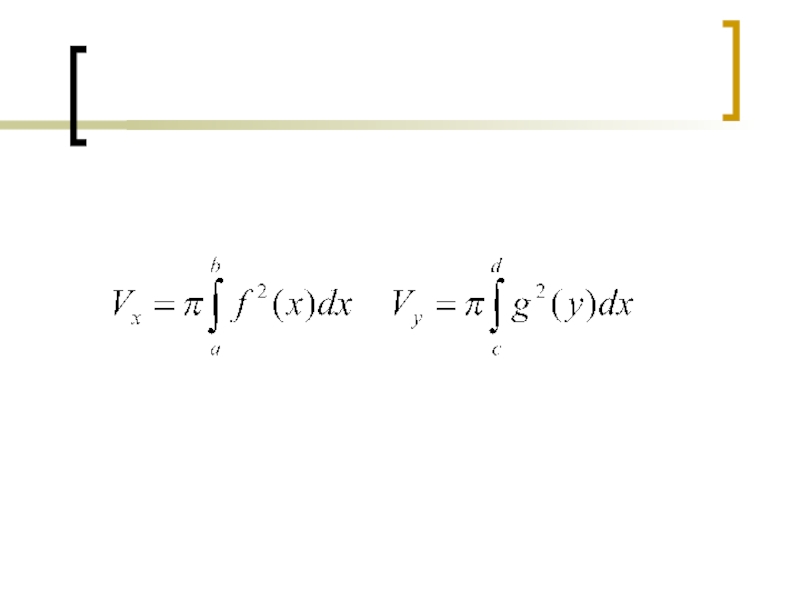- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на темуГеометрическое приложение определенного интеграла
Содержание
- 1. Презентация по математике на темуГеометрическое приложение определенного интеграла
- 2. Укажите соответствующую функцию для графика1111А)Б)В)Г)Д)Е)У= х2y= log2xy= 2x
- 3. Указать первообразные для функции
- 4. Найти ошибки +С
- 5. Формула Ньютона - ЛейбницаФормула Ньютона - Лейбница
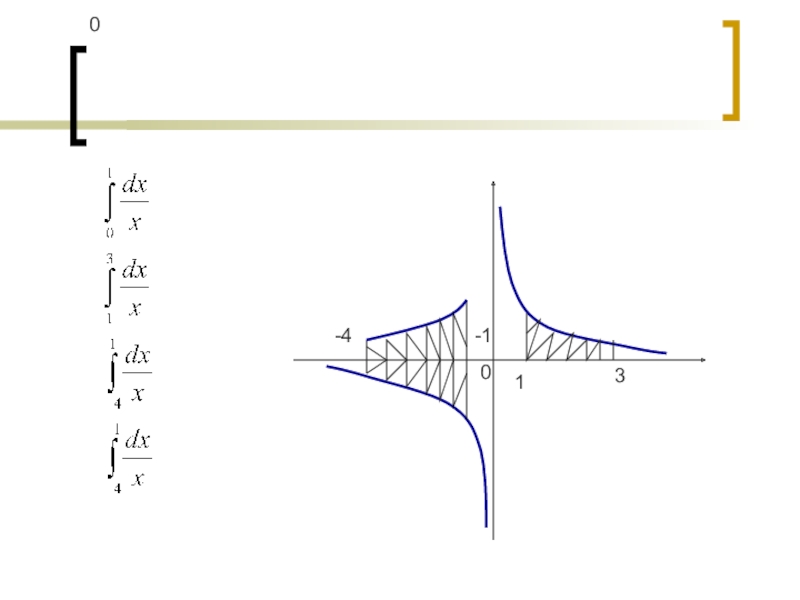
- 6. х≠0х≠0х≠0
- 7. 001-43-1
- 8. Геометрическое приложение определенного интеграла
- 9. Площадь плоской фигуры
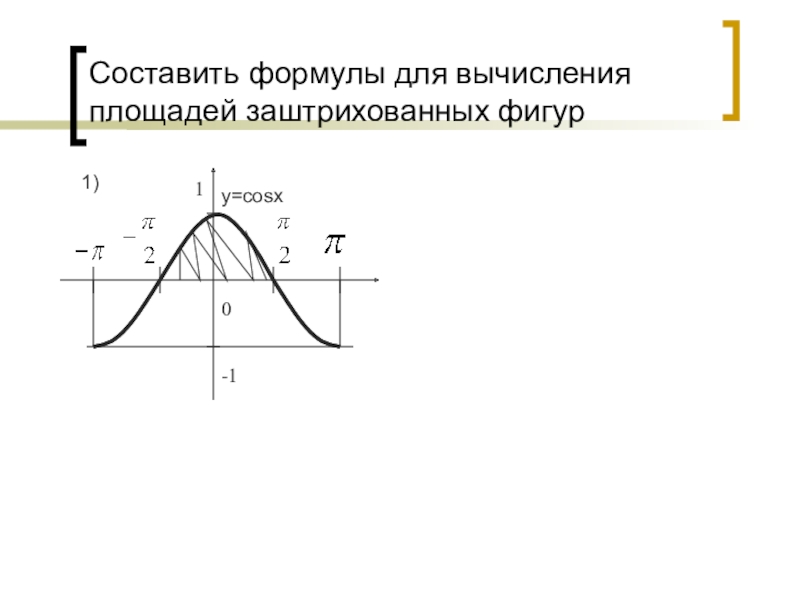
- 10. Составить формулы для вычисления площадей заштрихованных фигур-110y=cosx1)
- 11. -1-110y=sinx2)
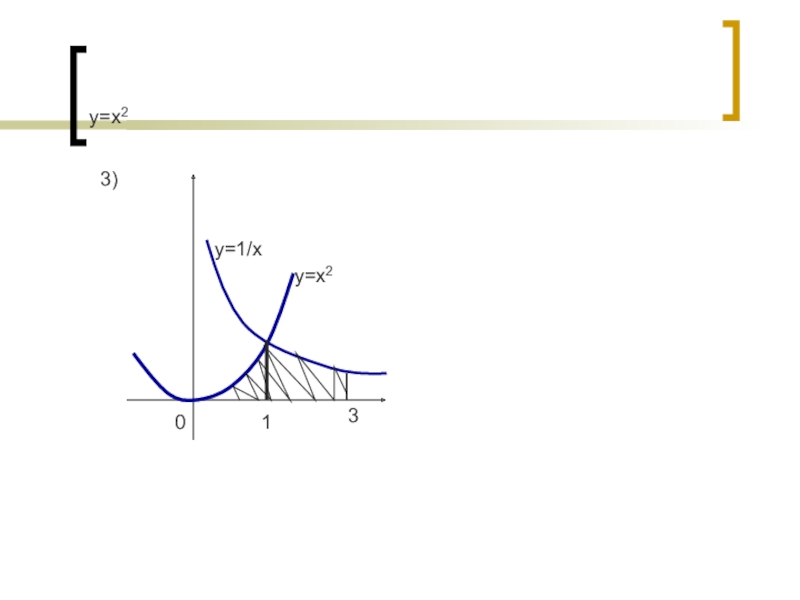
- 12. y=x213)
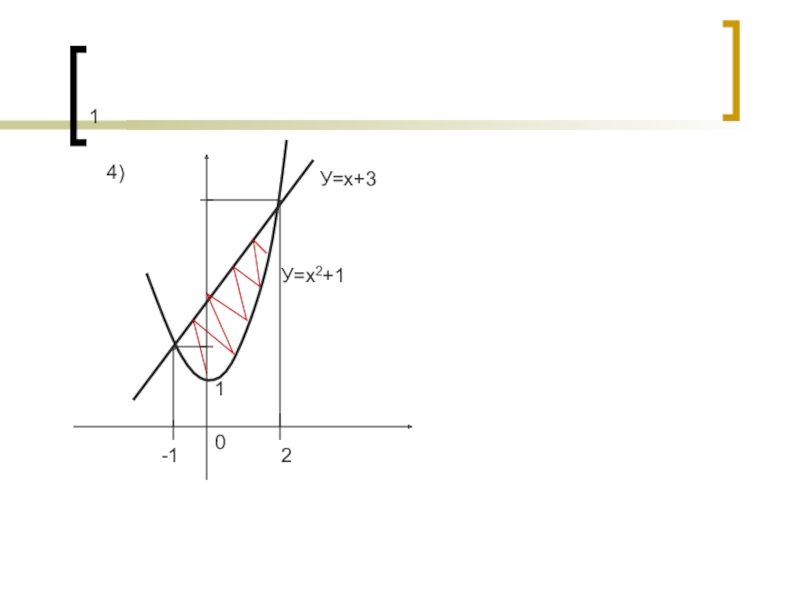
- 13. 1-124)
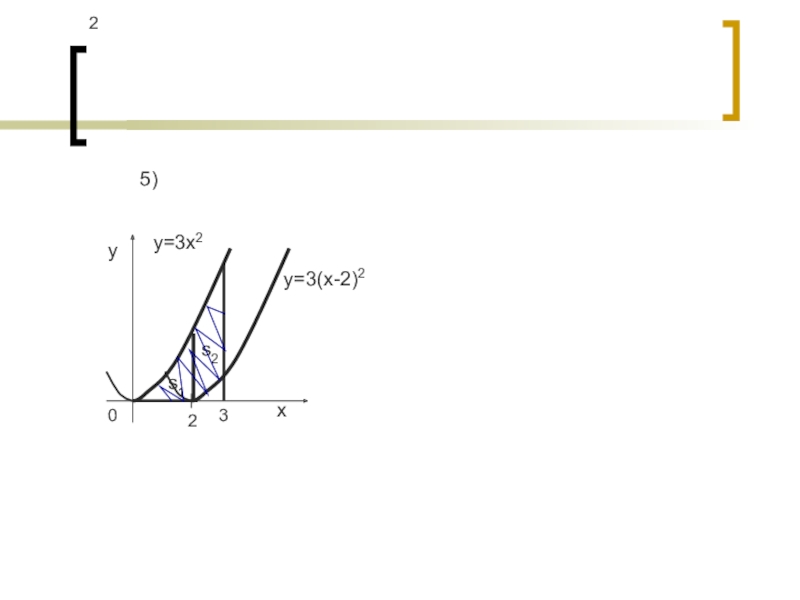
- 14. 22s2s10y=3x23y=3(x-2)2xy5)
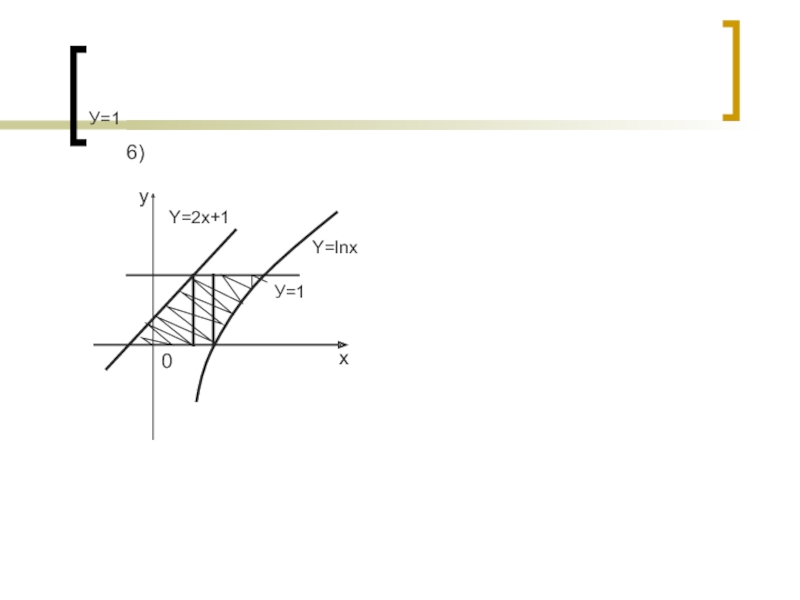
- 15. У=16)
- 16. Домашнее задание Вычислить площади для рисунков с1
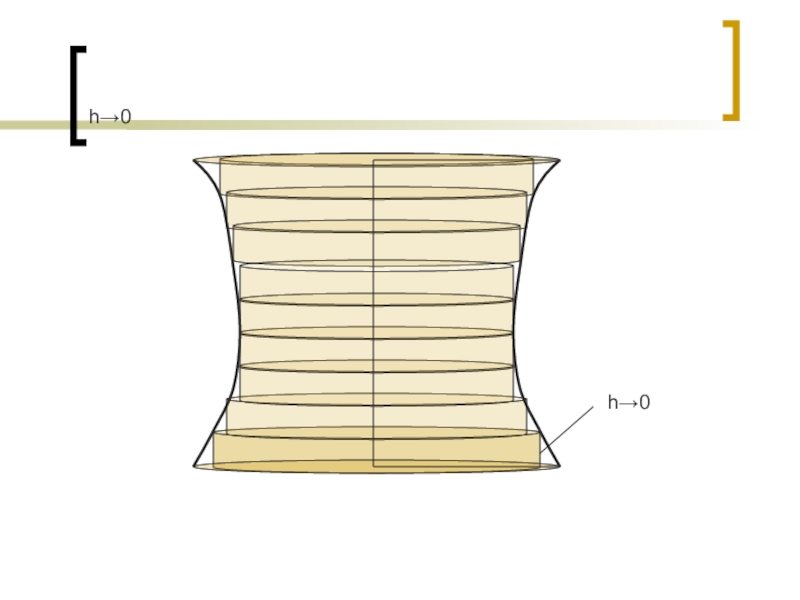
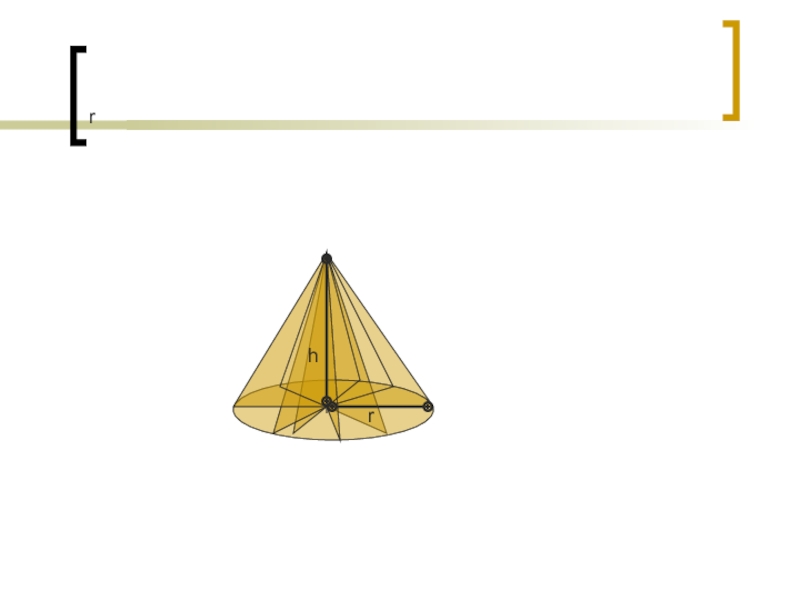
- 17. Объем тела вращения
- 18. Слайд 18
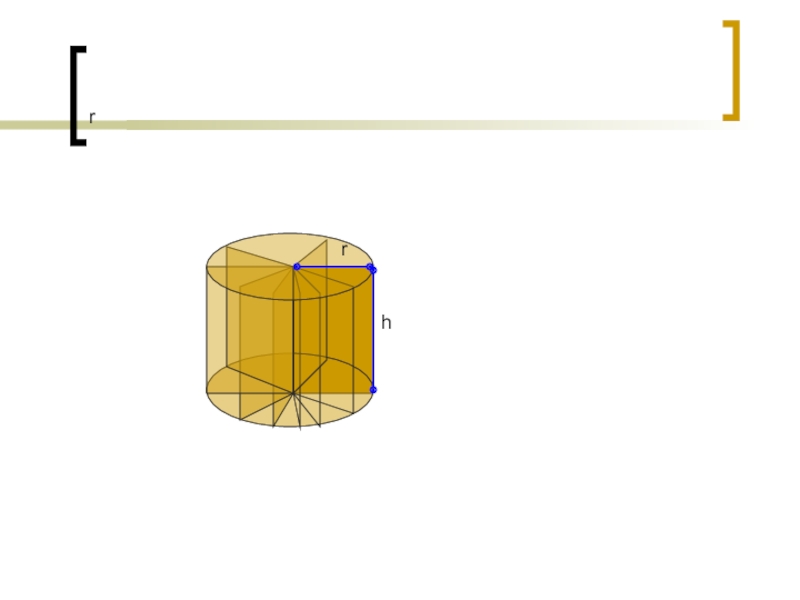
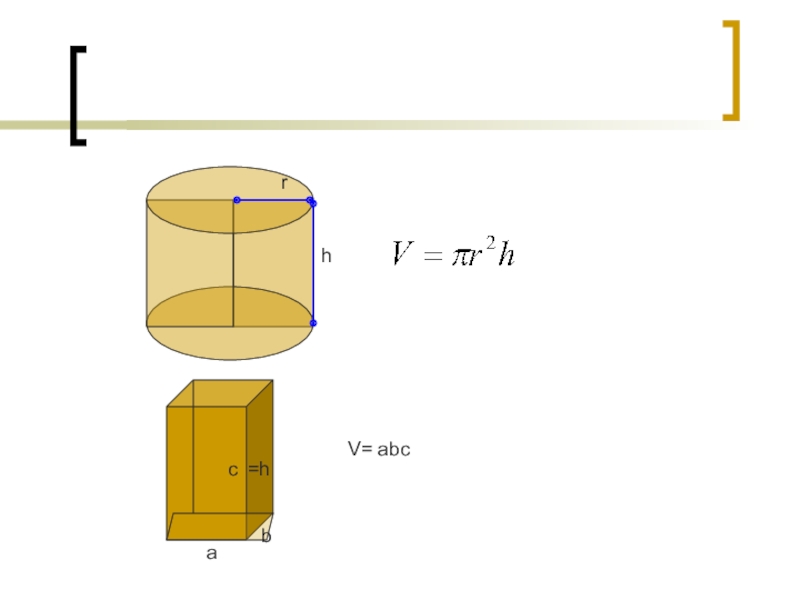
- 19. rrh
- 20. rrh
- 21. V= abc = Sh=h
- 22. Y=f(x) – непрерывна и знакопостоянна на отрезке [a, b]авхiR=f(xi)y=f(x)
- 23. h→0h→0
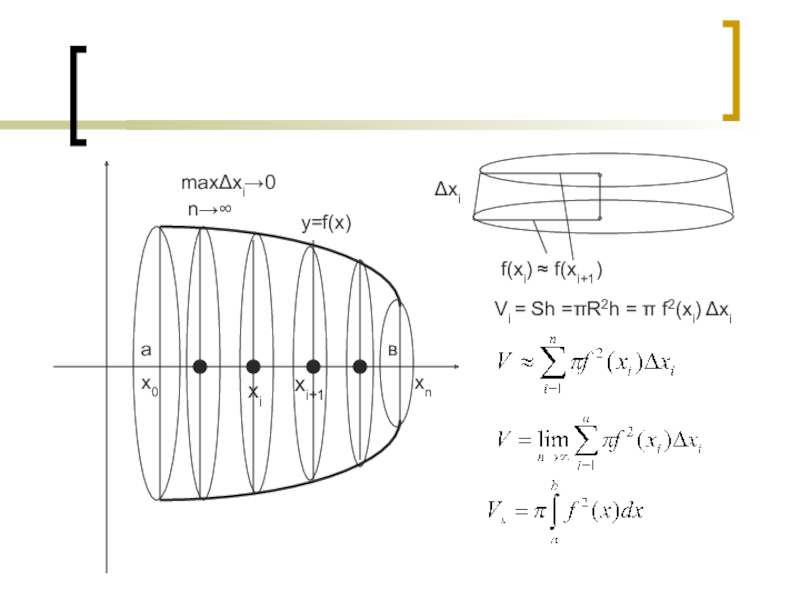
- 24. авхixi+1maxΔxi→0Δxif(xi) ≈ f(xi+1) Vi = Sh =πR2h = π f2(xi) Δxix0xnn→∞y=f(x)
- 25. ххусdx=g(y)
- 26. Слайд 26
- 27. 80ху2х=у3
- 28. Найти объем тела, полученного вращением плоской фигуры,
- 29. Найти объем тела, полученного вращением плоской фигуры
- 30. Найти объем тела, полученного вращением плоской фигуры
- 31. Найти объем тела, полученного вращением плоской фигуры вокруг ох, ограниченной линиями у = х2 и ху
- 32. Домашнее заданиеНайти объем тела, полученного вращением плоской
Укажите соответствующую функцию для графика1111А)Б)В)Г)Д)Е)У= х2y= log2xy= 2x
Слайд 16Домашнее задание
Вычислить площади для рисунков с1 по4
Найти площадь фигуры, ограниченной
линиями
1) y=lnx, y=3x+4, y=-1, y=1
2) y=x2+5x-6, y=-x2-5x+22
Найти интегралы
1) y=lnx, y=3x+4, y=-1, y=1
2) y=x2+5x-6, y=-x2-5x+22
Найти интегралы
Слайд 28
Найти объем тела, полученного вращением плоской фигуры, ограниченной осью х, прямыми
у = 3х, х=3
вокруг оси х
вокруг оси х
х
у
Слайд 29Найти объем тела, полученного вращением плоской фигуры вокруг оу, ограниченной линиями
у = lgx , y=0, y=1
Найти объем тела, полученного вращением плоской фигуры вокруг оу, ограниченной линиями у = lgx , y=0, y=1
x
y
Слайд 30
Найти объем тела, полученного вращением плоской фигуры вокруг оси х, ограниченной
верхней полуокружностью х2 + у2 =25
х
у
5
0
-5
Слайд 31
Найти объем тела, полученного вращением плоской фигуры вокруг ох, ограниченной линиями
у = х2 и
х
у
Слайд 32Домашнее задание
Найти объем тела, полученного вращением плоской фигуры вокруг ох ,
ограниченной линиями у = х2 , х=2, х=4
Найти объем тела, полученного вращением плоской фигуры вокруг ох, ограниченной линиями y= cosx, осью х,
Найти объем тела, полученного вращением плоской фигуры вокруг ох и оу, ограниченной линиями у = х3 и у=4х
Найти объем тела, полученного вращением плоской фигуры вокруг ох, ограниченной линиями y= cosx, осью х,
Найти объем тела, полученного вращением плоской фигуры вокруг ох и оу, ограниченной линиями у = х3 и у=4х











![Презентация по математике на темуГеометрическое приложение определенного интеграла Y=f(x) – непрерывна и знакопостоянна на отрезке [a, b]авхiR=f(xi)y=f(x) Y=f(x) – непрерывна и знакопостоянна на отрезке [a, b]авхiR=f(xi)y=f(x)](/img/thumbs/09867975280d8725959b82d3a73e4acf-800x.jpg)