- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Экстремум функции (11 класс)
Содержание
- 1. Презентация по математике на тему Экстремум функции (11 класс)
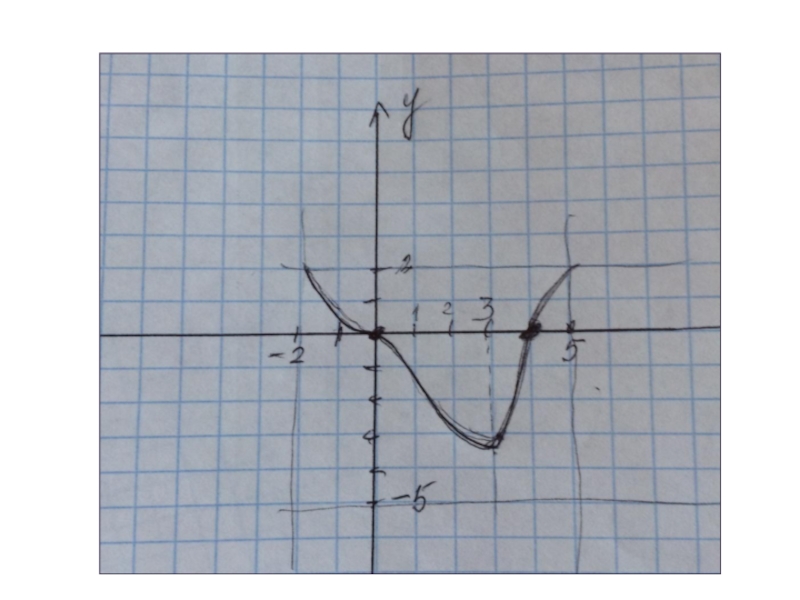
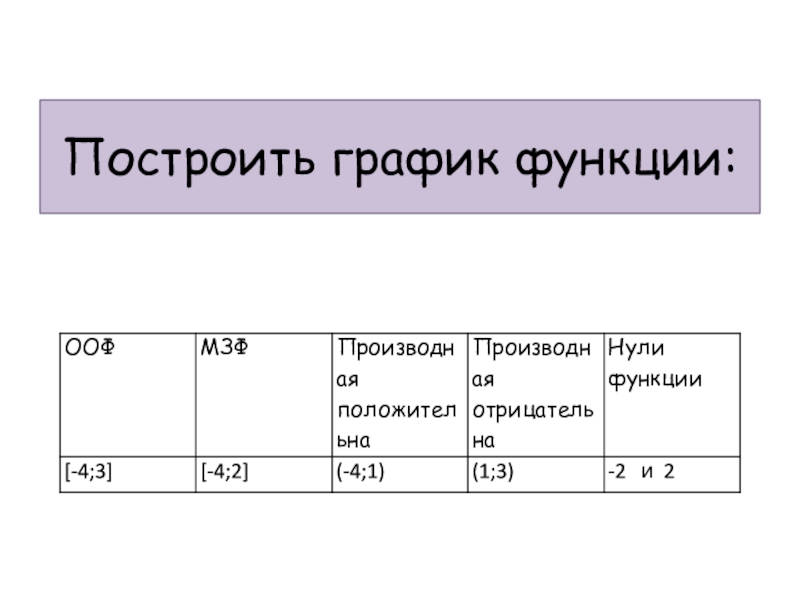
- 2. Построить график функции:
- 3. Слайд 3
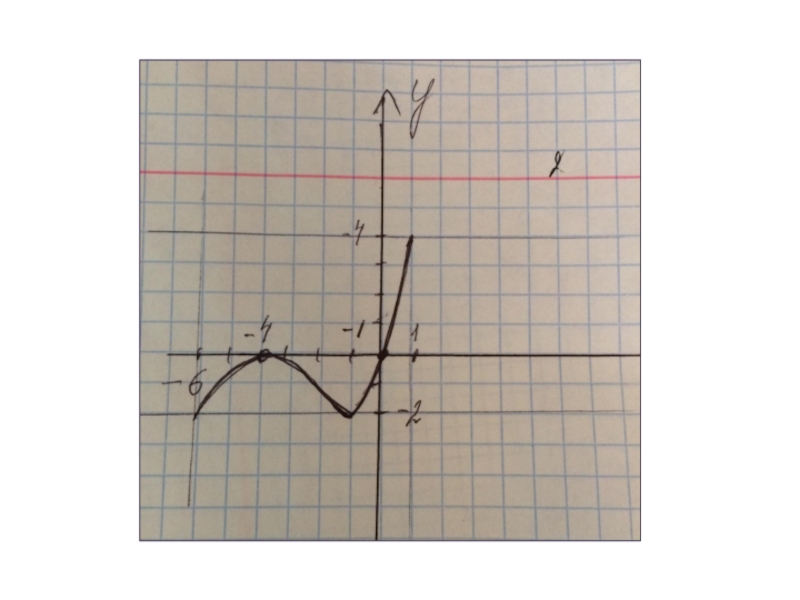
- 4. ООФ[-6;1]МЗФ[-2;4]Производная положительна(-6;-4)(-1;1)Производная отрицательна(-4;-1)Нули функции-4 и 0
- 5. Слайд 5
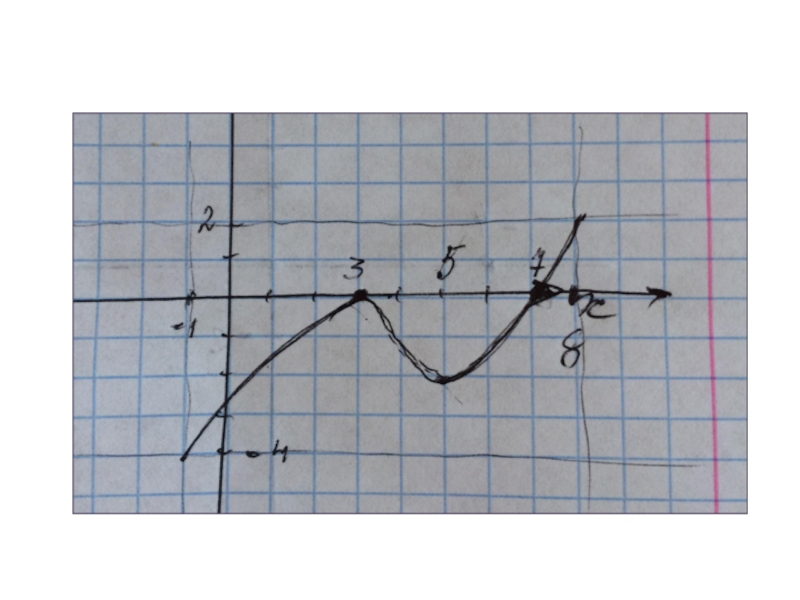
- 6. ООФ [-1;8]МЗФ [-4;2]Производная положительна (-1;3)(5;8)Производная отрицательна ( 3;5)Нули функции 3 и 7
- 7. Слайд 7
- 8. ООФ [-2;5]МЗФ [-4;4]Производная положительна (-2;0)(3;5)Производная отрицательна ( 0;3)Нули функции 0 и 4
- 9. Слайд 9
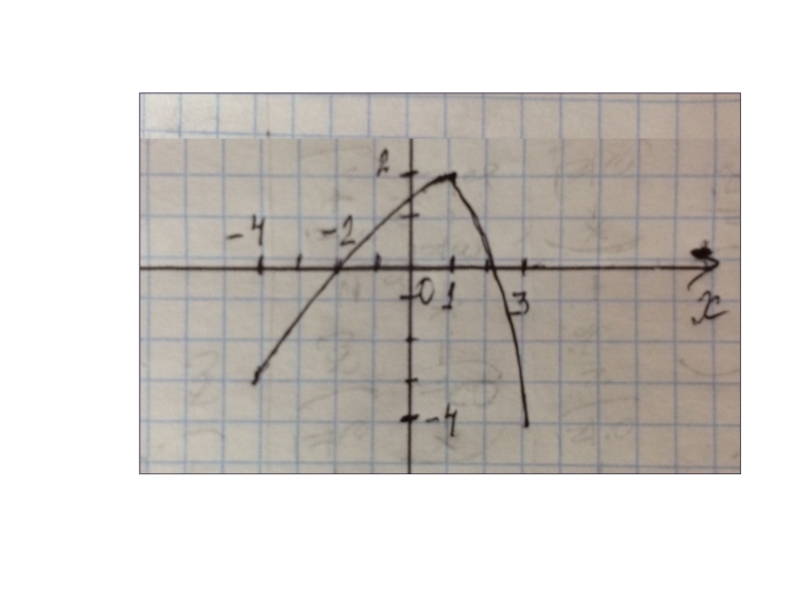
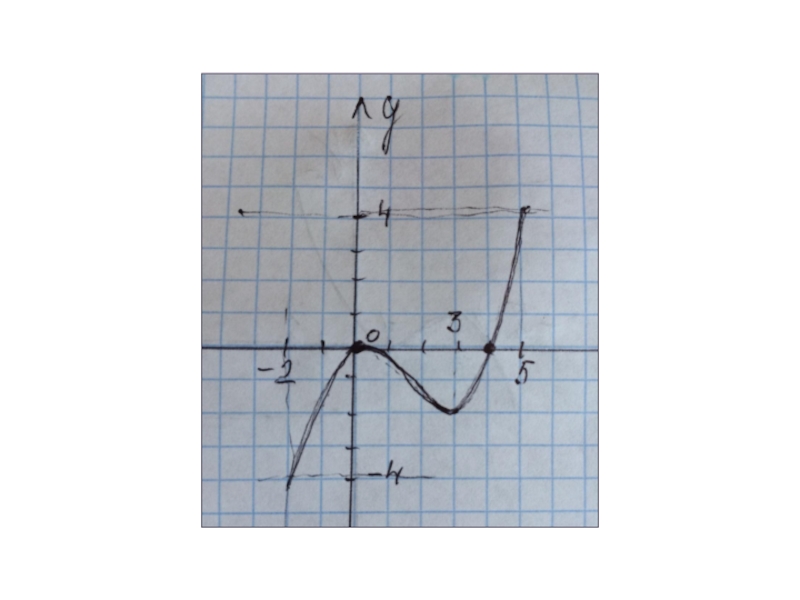
- 10. ООФ [-4;3]МЗФ [-5;3]Производная положительна
- 11. Слайд 11
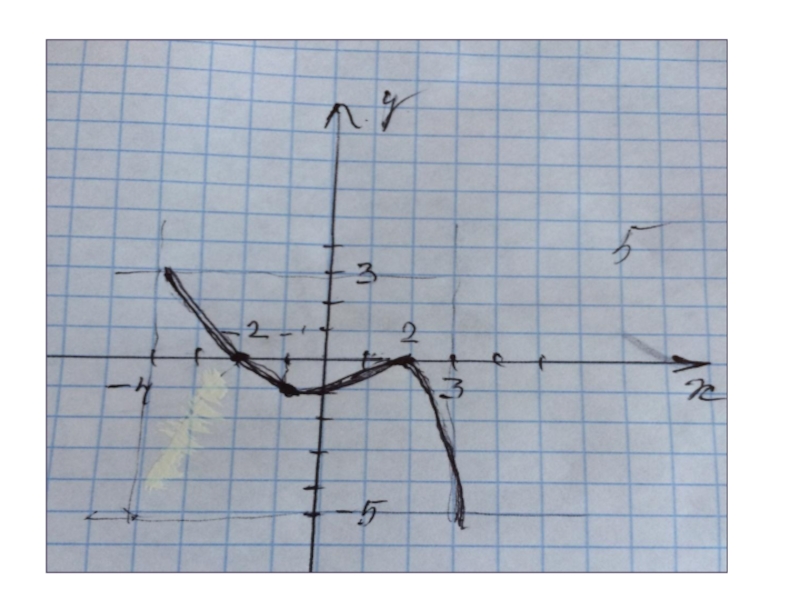
- 12. ООФ [-1;6]МЗФ [-4;4]Производная положительна (-1;3)Производная отрицательна ( 3;6) Нули функции 0и 5
- 13. Слайд 13
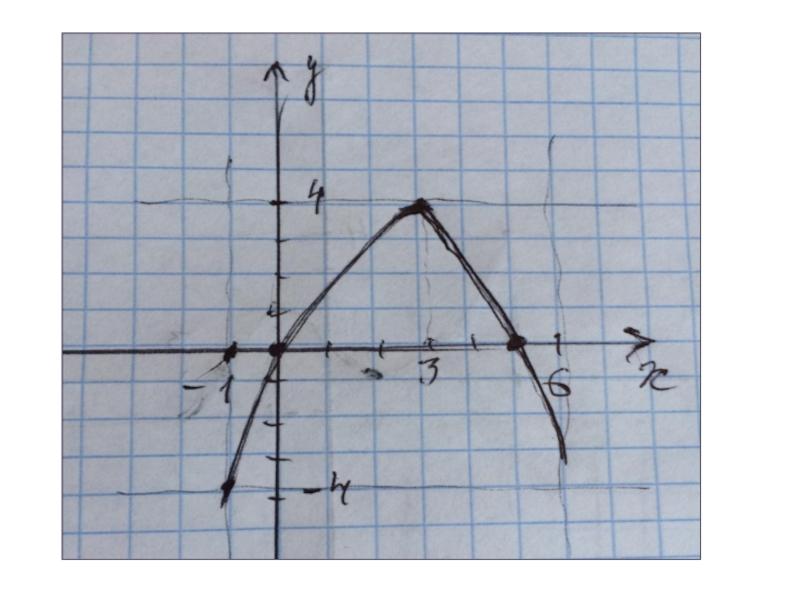
- 14. ООФ [-3;5]МЗФ [-3;4]Производная положительна (-3;4)Производная отрицательна ( 4;5) Нули функции -1
- 15. Слайд 15
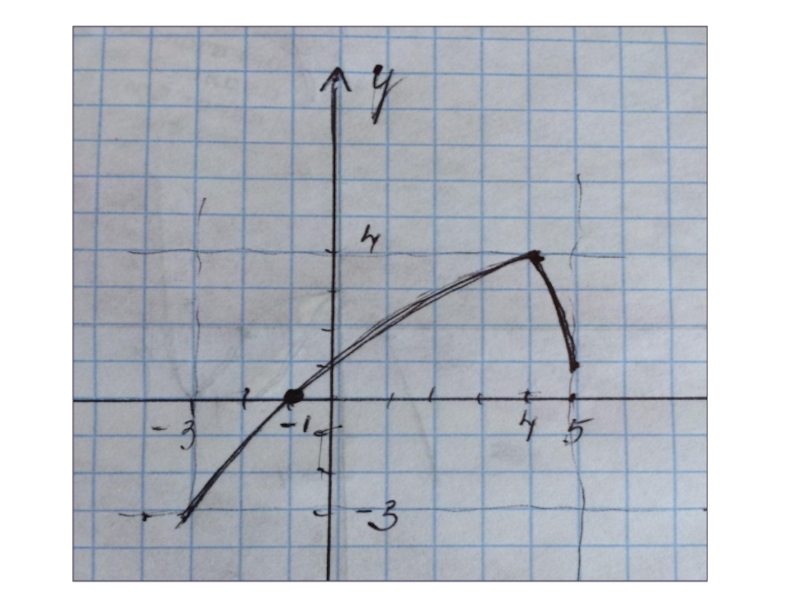
- 16. ООФ [-4;3]МЗФ [-1;4]Производная положительна
- 17. Слайд 17
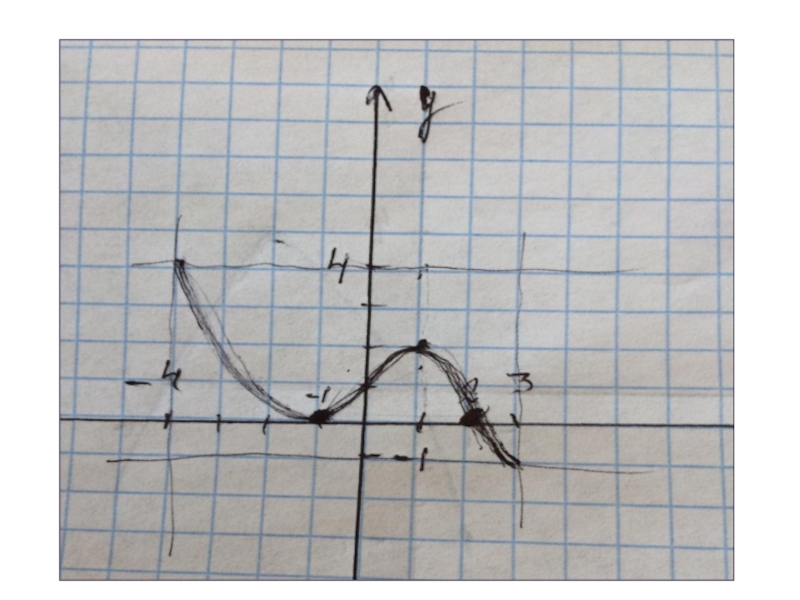
- 18. ООФ [-5;2]МЗФ [-2;5]Производная положительна
- 19. Слайд 19
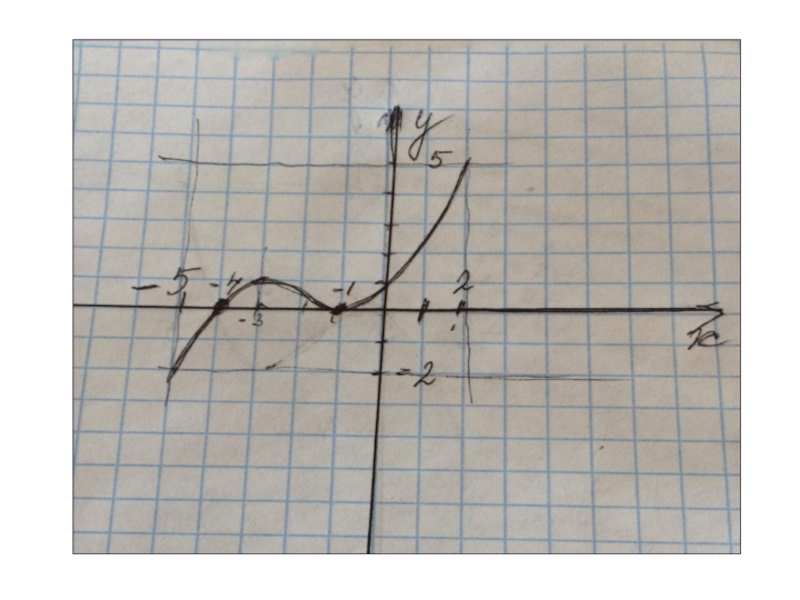
- 20. ООФ [-2;4]МЗФ [-4;4]Производная положительна
- 21. Слайд 21
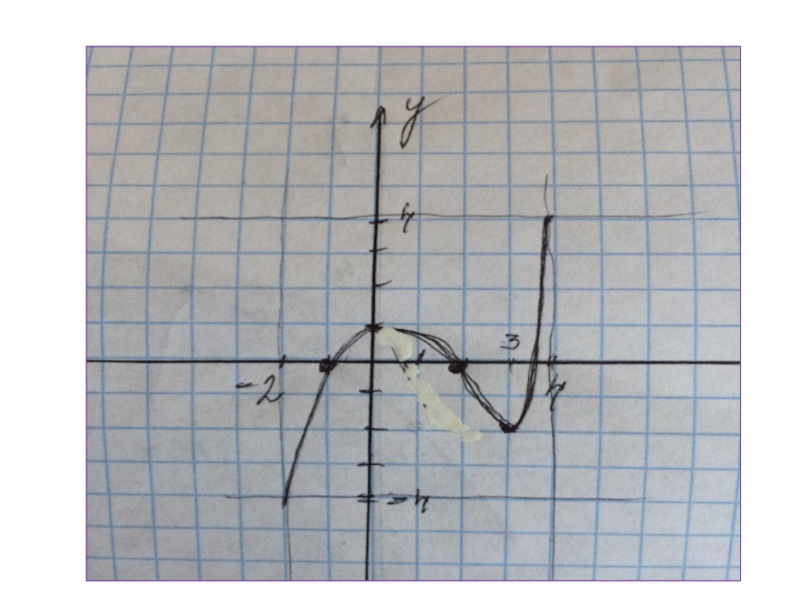
- 22. ООФ [-5;4]МЗФ [-4;5]Производная положительна
- 23. Слайд 23
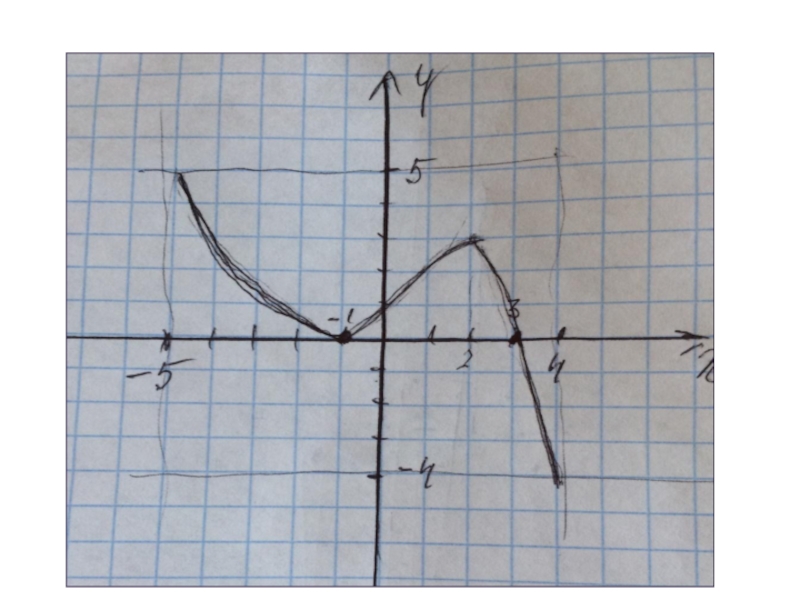
- 24. ООФ [-2;5]МЗФ [-5;2]Производная положительна
- 25. Слайд 25
- 26. Если при переходе через точку Х 0
- 27. 1)Точки ,в которых производная равна нулю называются
- 28. - Х 1-точка минимума,стационарная (производная равна
- 29. Слайд 29
- 30. Слайд 30
Построить график функции:
Слайд 1Применение производной к исследованию функций
Экстремумы функций
Учитель математики МБОУ «СОШ №12»:Тарасова Л.В.
Слайд 4ООФ[-6;1]
МЗФ[-2;4]
Производная положительна(-6;-4)(-1;1)
Производная отрицательна(-4;-1)
Нули функции-4 и 0
Слайд 6ООФ [-1;8]
МЗФ [-4;2]
Производная положительна (-1;3)(5;8)
Производная отрицательна (
3;5)
Нули функции 3 и 7
Нули функции 3 и 7
Слайд 8ООФ [-2;5]
МЗФ [-4;4]
Производная положительна (-2;0)(3;5)
Производная отрицательна (
0;3)
Нули функции 0 и 4
Нули функции 0 и 4
Слайд 10ООФ [-4;3]
МЗФ [-5;3]
Производная положительна (-1;2)
Производная отрицательна (
-4;-1) ( 2;3)
Нули функции -2и 2
Нули функции -2и 2
Слайд 12ООФ [-1;6]
МЗФ [-4;4]
Производная положительна (-1;3)
Производная отрицательна (
3;6)
Нули функции 0и 5
Нули функции 0и 5
Слайд 14ООФ [-3;5]
МЗФ [-3;4]
Производная положительна (-3;4)
Производная отрицательна (
4;5)
Нули функции -1
Нули функции -1
Слайд 16ООФ [-4;3]
МЗФ [-1;4]
Производная положительна (-1;1)
Производная отрицательна (
-4;-1) ( 1;3)
Нули функции -1и 2
Нули функции -1и 2
Слайд 18ООФ [-5;2]
МЗФ [-2;5]
Производная положительна (-5;-3) ( -1;2)
Производная отрицательна
( -3;-1)
Нули функции -4 и -1
Нули функции -4 и -1
Слайд 20ООФ [-2;4]
МЗФ [-4;4]
Производная положительна (-2;0) ( 3;4)
Производная отрицательна
( 0;3)
Нули функции -1 и 2
Нули функции -1 и 2
Слайд 22ООФ [-5;4]
МЗФ [-4;5]
Производная положительна ( -1;2)
Производная отрицательна
( -5;-1) ( 2;4)
Нули функции -1 и 3
Нули функции -1 и 3
Слайд 24ООФ [-2;5]
МЗФ [-5;2]
Производная положительна ( 3;5)
Производная отрицательна
( -2;0) ( 0;3)
Нули функции 0 и 4
Нули функции 0 и 4
Слайд 26Если при переходе через точку Х 0 :
-производная меняет знак с
«+»на «-»,
то Х 0 – точка максимума.
-производная меняет знак с «-»на «+»,
то Х 0 – точка минимума.
-производная не меняет знак ,
то Х 0 – точка перегиба.
то Х 0 – точка максимума.
-производная меняет знак с «-»на «+»,
то Х 0 – точка минимума.
-производная не меняет знак ,
то Х 0 – точка перегиба.
Слайд 271)
Точки ,в которых производная равна нулю называются стационарные.
2)
Точки ,в которых
производная равна нулю или недифференцируема называются критические.
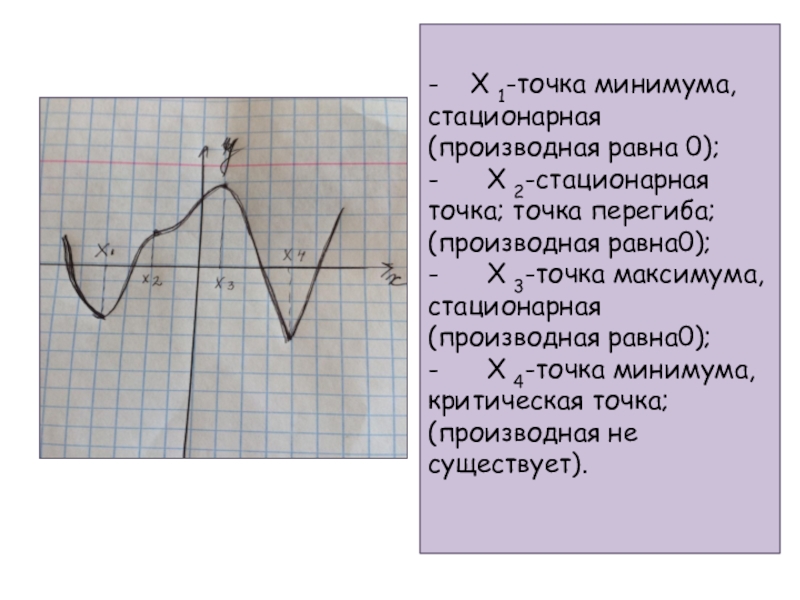
Слайд 28- Х 1-точка минимума,стационарная (производная равна 0); - Х 2-стационарная
точка; точка перегиба; (производная равна0);
- Х 3-точка максимума,стационарная (производная равна0);
- Х 4-точка минимума,
критическая точка; (производная не существует).
Слайд 29
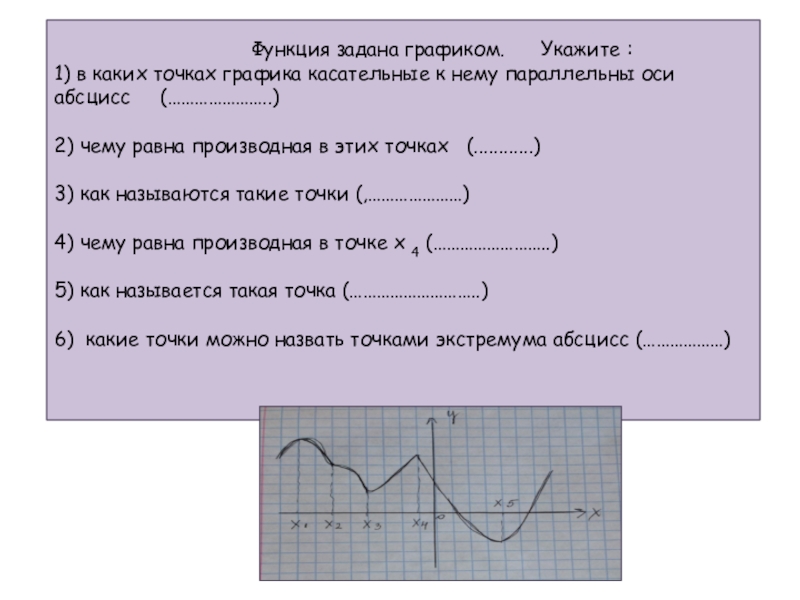
Функция задана графиком. Укажите :
1) в каких точках графика касательные к нему параллельны оси абсцисс (…………………..)
2) чему равна производная в этих точках (............)
3) как называются такие точки (,…………………)
4) чему равна производная в точке х 4 (……………………..)
5) как называется такая точка (………………………..)
6) какие точки можно назвать точками экстремума абсцисс (………………)
Слайд 30
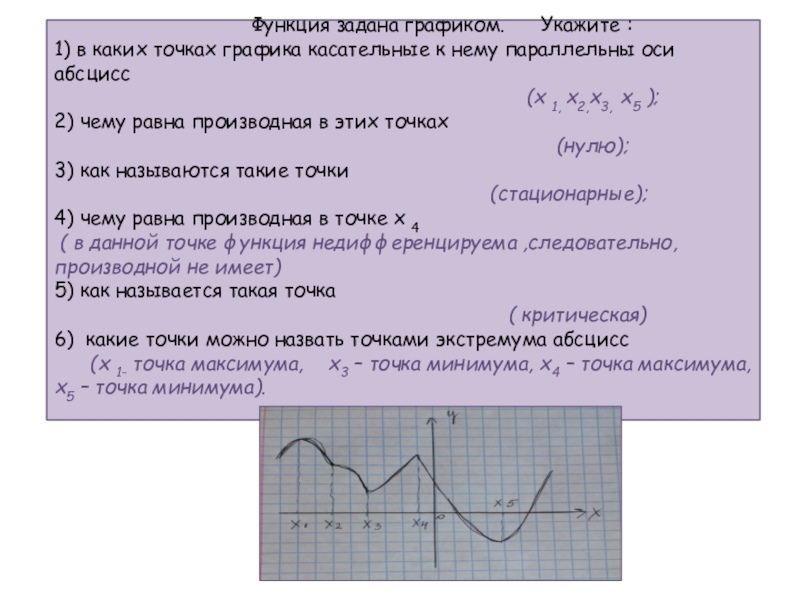
Функция задана графиком. Укажите :
1) в каких точках графика касательные к нему параллельны оси абсцисс
(х 1, х2,х3, х5 );
2) чему равна производная в этих точках
(нулю);
3) как называются такие точки
(стационарные);
4) чему равна производная в точке х 4
( в данной точке функция недифференцируема ,следовательно, производной не имеет)
5) как называется такая точка
( критическая)
6) какие точки можно назвать точками экстремума абсцисс
(х 1- точка максимума, х3 – точка минимума, х4 – точка максимума, х5 – точка минимума).

![Презентация по математике на тему Экстремум функции (11 класс) ООФ[-6;1]МЗФ[-2;4]Производная положительна(-6;-4)(-1;1)Производная отрицательна(-4;-1)Нули функции-4 и 0 ООФ[-6;1]МЗФ[-2;4]Производная положительна(-6;-4)(-1;1)Производная отрицательна(-4;-1)Нули функции-4 и 0](/img/tmb/5/436334/54a45ef1a4779dccd3a0068680edba67-800x.jpg)
![Презентация по математике на тему Экстремум функции (11 класс) ООФ [-1;8]МЗФ [-4;2]Производная положительна (-1;3)(5;8)Производная отрицательна ( 3;5)Нули функции 3 и 7 ООФ [-1;8]МЗФ [-4;2]Производная положительна (-1;3)(5;8)Производная отрицательна ( 3;5)Нули функции 3 и 7](/img/tmb/5/436334/eb15ed39e25206320e4323517cbbc251-800x.jpg)
![Презентация по математике на тему Экстремум функции (11 класс) ООФ [-2;5]МЗФ [-4;4]Производная положительна (-2;0)(3;5)Производная отрицательна ( 0;3)Нули функции 0 и 4 ООФ [-2;5]МЗФ [-4;4]Производная положительна (-2;0)(3;5)Производная отрицательна ( 0;3)Нули функции 0 и 4](/img/thumbs/c51532f84d88bc944132f87a0fe246f5-800x.jpg)
![Презентация по математике на тему Экстремум функции (11 класс) ООФ [-4;3]МЗФ [-5;3]Производная положительна (-1;2)Производная отрицательна ( -4;-1) ( 2;3)Нули функции -2и 2 ООФ [-4;3]МЗФ [-5;3]Производная положительна (-1;2)Производная отрицательна ( -4;-1) ( 2;3)Нули функции -2и 2](/img/thumbs/472d8d2dcd61af4926ec835d4eac1953-800x.jpg)
![Презентация по математике на тему Экстремум функции (11 класс) ООФ [-1;6]МЗФ [-4;4]Производная положительна (-1;3)Производная отрицательна ( 3;6) Нули функции 0и 5 ООФ [-1;6]МЗФ [-4;4]Производная положительна (-1;3)Производная отрицательна ( 3;6) Нули функции 0и 5](/img/thumbs/ca09368bfad4ad0f7281c3c23bae86da-800x.jpg)
![Презентация по математике на тему Экстремум функции (11 класс) ООФ [-3;5]МЗФ [-3;4]Производная положительна (-3;4)Производная отрицательна ( 4;5) Нули функции -1 ООФ [-3;5]МЗФ [-3;4]Производная положительна (-3;4)Производная отрицательна ( 4;5) Нули функции -1](/img/thumbs/08d7e9426f0079d8c838147c61b0fac5-800x.jpg)
![Презентация по математике на тему Экстремум функции (11 класс) ООФ [-4;3]МЗФ [-1;4]Производная положительна (-1;1)Производная отрицательна ( -4;-1) ( 1;3)Нули функции -1и 2 ООФ [-4;3]МЗФ [-1;4]Производная положительна (-1;1)Производная отрицательна ( -4;-1) ( 1;3)Нули функции -1и 2](/img/thumbs/751c1ba247b2d448d4d06debb043f8ba-800x.jpg)
![Презентация по математике на тему Экстремум функции (11 класс) ООФ [-5;2]МЗФ [-2;5]Производная положительна (-5;-3) ( -1;2)Производная отрицательна ( -3;-1)Нули функции -4 и -1 ООФ [-5;2]МЗФ [-2;5]Производная положительна (-5;-3) ( -1;2)Производная отрицательна ( -3;-1)Нули функции -4 и](/img/thumbs/d48056dec1c8d5a6d051da4c7025b420-800x.jpg)
![Презентация по математике на тему Экстремум функции (11 класс) ООФ [-2;4]МЗФ [-4;4]Производная положительна (-2;0) ( 3;4)Производная отрицательна ( 0;3)Нули функции -1 и 2 ООФ [-2;4]МЗФ [-4;4]Производная положительна (-2;0) ( 3;4)Производная отрицательна ( 0;3)Нули функции -1 и](/img/thumbs/51b30857e3935804a9372d87797f5d0c-800x.jpg)
![Презентация по математике на тему Экстремум функции (11 класс) ООФ [-5;4]МЗФ [-4;5]Производная положительна ( -1;2)Производная отрицательна ( -5;-1) ( 2;4)Нули функции -1 и 3 ООФ [-5;4]МЗФ [-4;5]Производная положительна ( -1;2)Производная отрицательна ( -5;-1) ( 2;4)Нули функции -1](/img/tmb/5/436334/efa7b169845849895e3c545cd163eb27-800x.jpg)
![Презентация по математике на тему Экстремум функции (11 класс) ООФ [-2;5]МЗФ [-5;2]Производная положительна ( 3;5)Производная отрицательна ( -2;0) ( 0;3)Нули функции 0 и 4 ООФ [-2;5]МЗФ [-5;2]Производная положительна ( 3;5)Производная отрицательна ( -2;0) ( 0;3)Нули функции 0](/img/thumbs/227aebeb8adcd1718a78c0eba9b252d0-800x.jpg)