математики Юрьева О.А. МБОУ «СОШ №6» г. Нефтеюганск
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Чтение графиков функций
Содержание
- 1. Презентация по математике на тему Чтение графиков функций
- 2. 1) Найдите значение с по графику функции у = aх² + bх+3, изображенному на рисунке
- 3. Значение с — это значение функции или
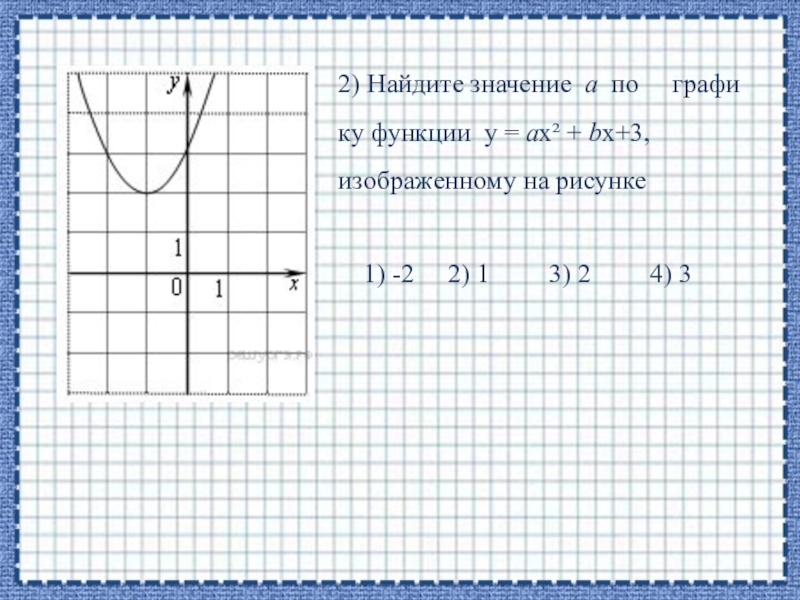
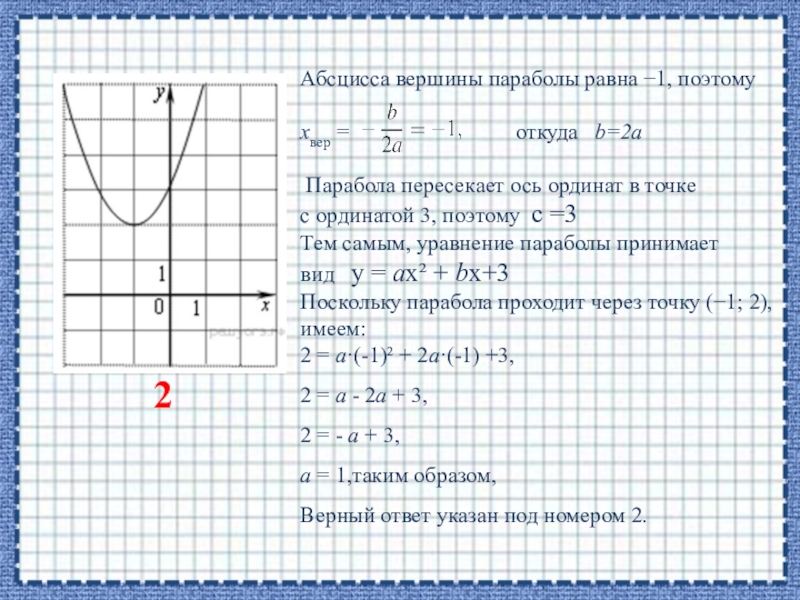
- 4. 2) Найдите значение a по графику функции у = aх² + bх+3,изображенному на рисунке
- 5. Абсцисса вершины параболы равна −1, поэтомухвер =
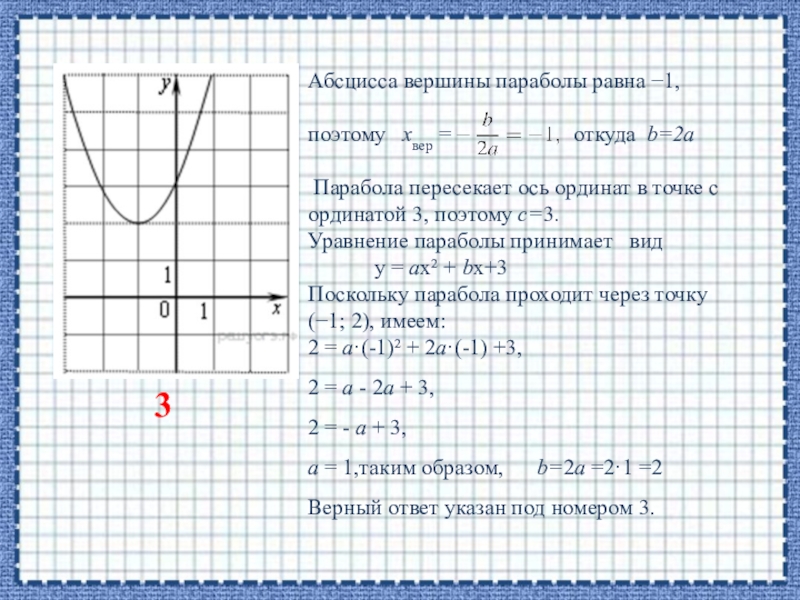
- 6. 3) Найдите значение b по графику
- 7. Абсцисса вершины параболы равна −1,
- 8. Слайд 8
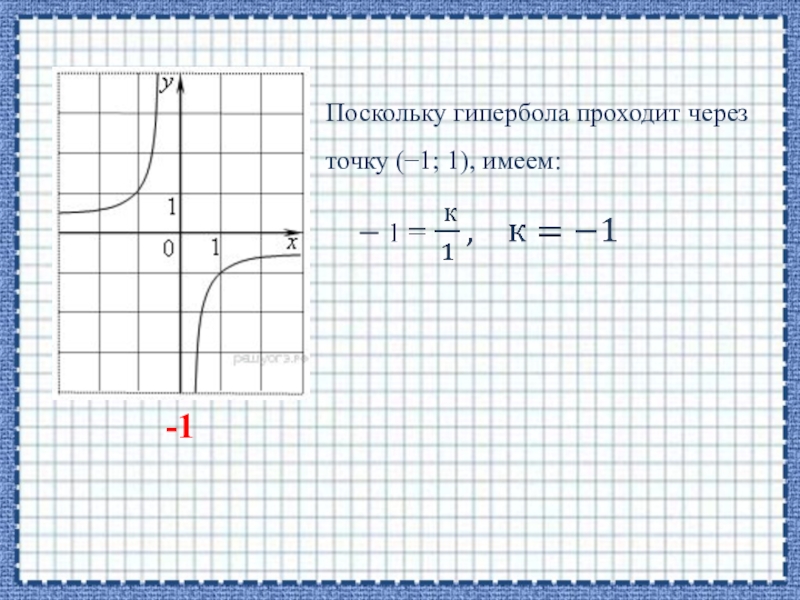
- 9. Поскольку гипербола проходит через точку (−1; 1), имеем: -1
- 10. и 5) На рисунке изображён график
- 11. и Проверим каждое из утверждений.функция возрастает
- 12. 6) На рисунке изображён график квадратичной функции
- 13. Проверим каждое из утверждений.1) На луче (−∞;
- 14. 7) На рисунке изображён график квадратичной функции
- 15. Проверим каждое из утверждений.f (−1) = f(3) - это
- 16. 8) На рисунке изображён график квадратичной функции
- 17. 9) На рисунке изображён график функции y
- 18. 8) На рисунке изображён график функции y
- 19. 9) На рисунке изображены графики
- 20. График функции у = ax2 + bx + c — парабола.
- 21. Сайт «Решу ОГЭ», образовательный портал для подготовки к экзаменамhttps://math-oge.sdamgia.ru/test?theme=62Источник содержания:
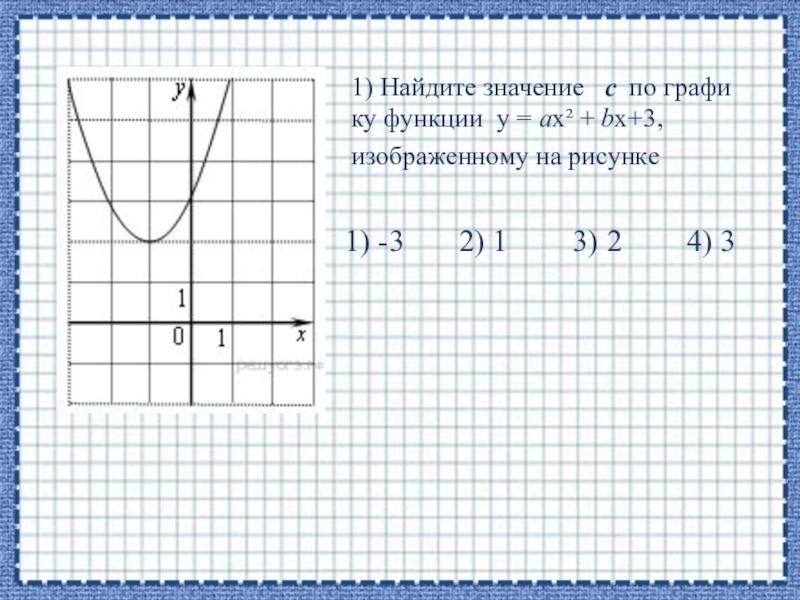
1) Найдите значение с по графику функции у = aх² + bх+3, изображенному на рисунке
Слайд 21) Найдите значение с по графику функции у = aх²
+ bх+3,
изображенному на рисунке
изображенному на рисунке
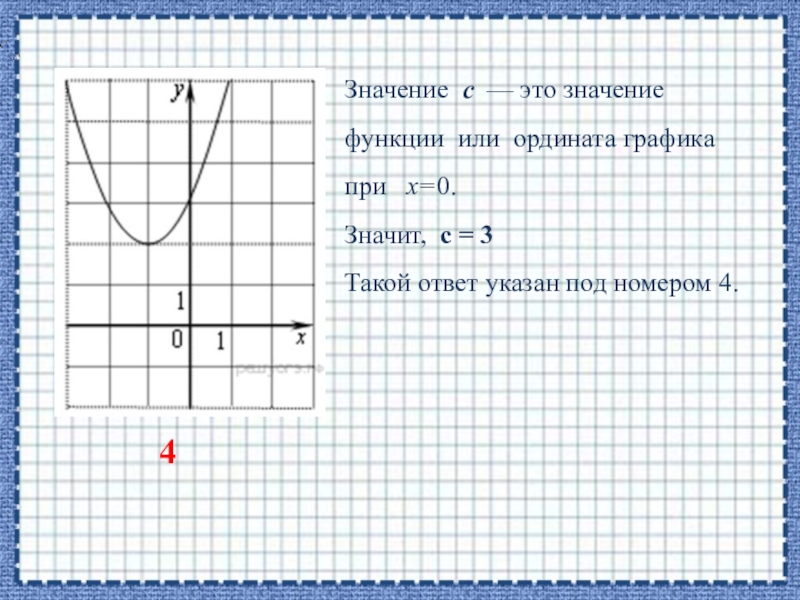
Слайд 3Значение с — это значение функции или ордината графика при
х=0.
Значит, с = 3
Такой ответ указан под номером 4.
Значит, с = 3
Такой ответ указан под номером 4.
4
Слайд 42) Найдите значение a по графику функции у =
aх² + bх+3,
изображенному на рисунке
изображенному на рисунке
Слайд 5
Абсцисса вершины параболы равна −1, поэтому
хвер =
откуда b=2a
Парабола пересекает ось ординат в точке
с ординатой 3, поэтому c =3
Тем самым, уравнение параболы принимает
вид у = aх² + bх+3
Поскольку парабола проходит через точку (−1; 2), имеем:
2 = a·(-1)² + 2а·(-1) +3,
2 = а - 2а + 3,
2 = - а + 3,
а = 1,таким образом,
Верный ответ указан под номером 2.
Парабола пересекает ось ординат в точке
с ординатой 3, поэтому c =3
Тем самым, уравнение параболы принимает
вид у = aх² + bх+3
Поскольку парабола проходит через точку (−1; 2), имеем:
2 = a·(-1)² + 2а·(-1) +3,
2 = а - 2а + 3,
2 = - а + 3,
а = 1,таким образом,
Верный ответ указан под номером 2.
2
Слайд 7
Абсцисса вершины параболы равна −1,
поэтому хвер =
откуда b=2a
Парабола пересекает ось ординат в точке с ординатой 3, поэтому c=3.
Уравнение параболы принимает вид
у = aх² + bх+3
Поскольку парабола проходит через точку
(−1; 2), имеем:
2 = a·(-1)² + 2а·(-1) +3,
2 = а - 2а + 3,
2 = - а + 3,
а = 1,таким образом, b=2a =2·1 =2
Верный ответ указан под номером 3.
Парабола пересекает ось ординат в точке с ординатой 3, поэтому c=3.
Уравнение параболы принимает вид
у = aх² + bх+3
Поскольку парабола проходит через точку
(−1; 2), имеем:
2 = a·(-1)² + 2а·(-1) +3,
2 = а - 2а + 3,
2 = - а + 3,
а = 1,таким образом, b=2a =2·1 =2
Верный ответ указан под номером 3.
3
Слайд 10 и
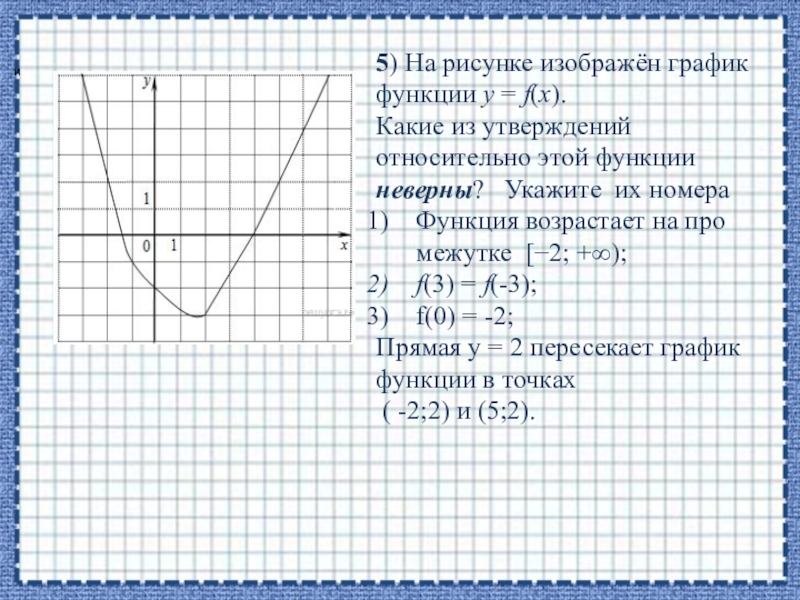
5) На рисунке изображён график функции y = f(x).
Какие из утверждений
относительно этой функции
неверны? Укажите их номера
Функция возрастает на промежутке [−2; +∞);
f(3) = f(-3);
f(0) = -2;
Прямая у = 2 пересекает график функции в точках
( -2;2) и (5;2).
неверны? Укажите их номера
Функция возрастает на промежутке [−2; +∞);
f(3) = f(-3);
f(0) = -2;
Прямая у = 2 пересекает график функции в точках
( -2;2) и (5;2).
Слайд 11 и
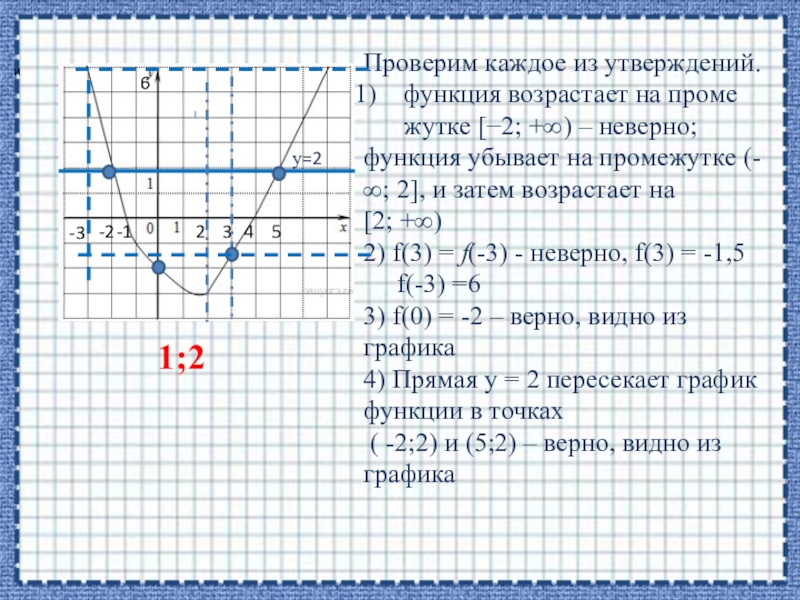
Проверим каждое из утверждений.
функция возрастает на промежутке [−2; +∞)
– неверно;
функция убывает на промежутке (- ∞; 2], и затем возрастает на
[2; +∞)
2) f(3) = f(-3) - неверно, f(3) = -1,5
f(-3) =6
3) f(0) = -2 – верно, видно из графика
4) Прямая у = 2 пересекает график функции в точках
( -2;2) и (5;2) – верно, видно из графика
функция убывает на промежутке (- ∞; 2], и затем возрастает на
[2; +∞)
2) f(3) = f(-3) - неверно, f(3) = -1,5
f(-3) =6
3) f(0) = -2 – верно, видно из графика
4) Прямая у = 2 пересекает график функции в точках
( -2;2) и (5;2) – верно, видно из графика
2
у=2
3
4
5
-1
-2
1;2
-3
6
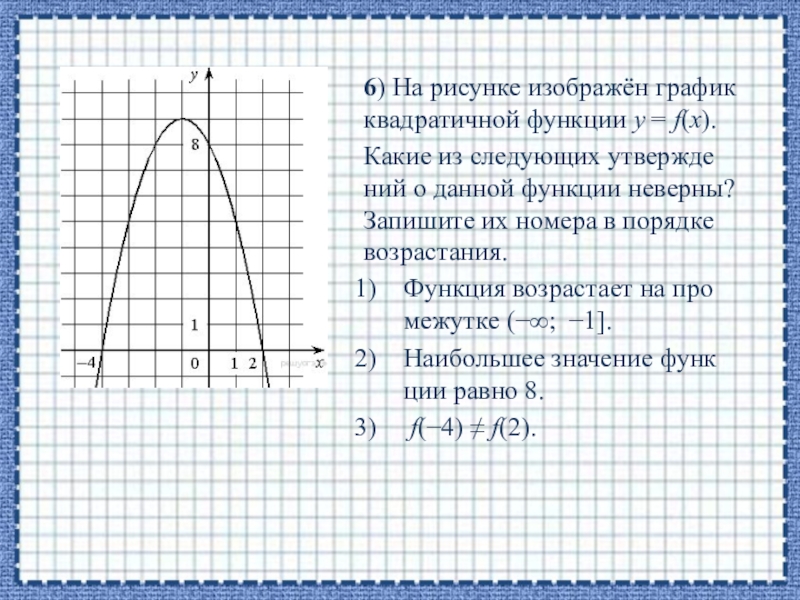
Слайд 126) На рисунке изображён график квадратичной функции y = f(x).
Какие из следующих утверждений
о данной функции неверны? Запишите их номера в порядке возрастания.
Функция возрастает на промежутке (−∞; −1].
Наибольшее значение функции равно 8.
f(−4) ≠ f(2).
Функция возрастает на промежутке (−∞; −1].
Наибольшее значение функции равно 8.
f(−4) ≠ f(2).
Слайд 13Проверим каждое из утверждений.
1) На луче (−∞; −1] большему значению аргумента
соответствует большее значение функции. Следовательно, функция возрастает на этом луче; утверждение верно.
2)Наибольшее значение функции равно 8- это утверждение неверно.
3) f(−4) ≠ f(2) - утверждение
неверно.
2)Наибольшее значение функции равно 8- это утверждение неверно.
3) f(−4) ≠ f(2) - утверждение
неверно.
23
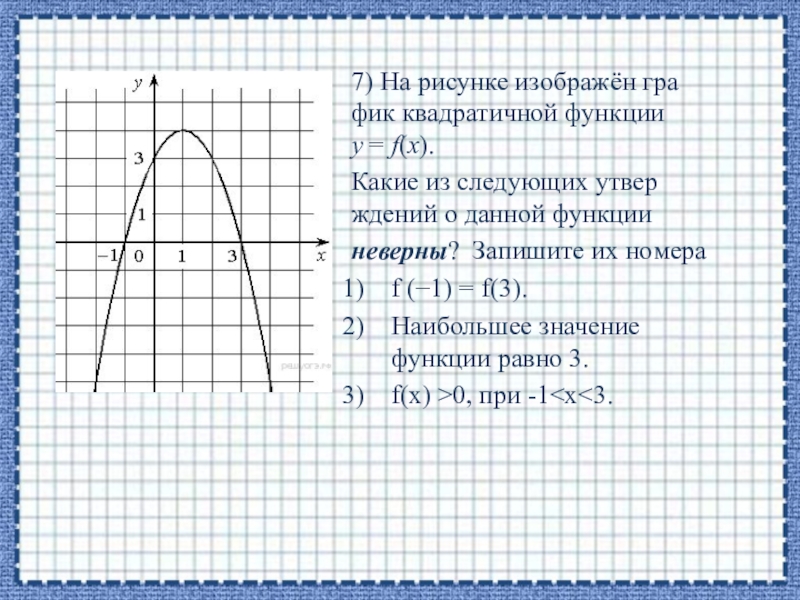
Слайд 147) На рисунке изображён график квадратичной функции y = f(x).
Какие из следующих утверждений
о данной функции
неверны? Запишите их номера
f (−1) = f(3).
Наибольшее значение функции равно 3.
f(х) >0, при -1<х<3.
неверны? Запишите их номера
f (−1) = f(3).
Наибольшее значение функции равно 3.
f(х) >0, при -1<х<3.
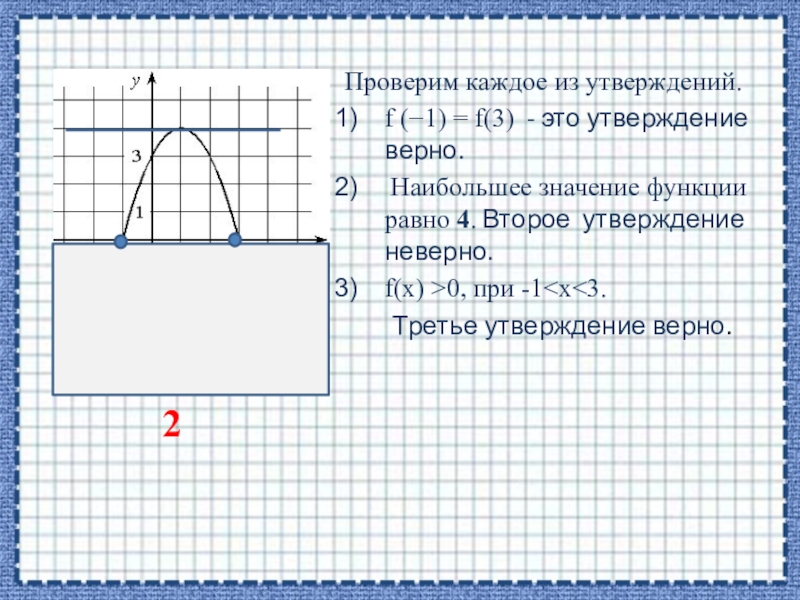
Слайд 15Проверим каждое из утверждений.
f (−1) = f(3) - это утверждение верно.
Наибольшее значение
функции равно 4. Второе утверждение неверно.
f(х) >0, при -1<х<3.
Третье утверждение верно.
f(х) >0, при -1<х<3.
Третье утверждение верно.
2
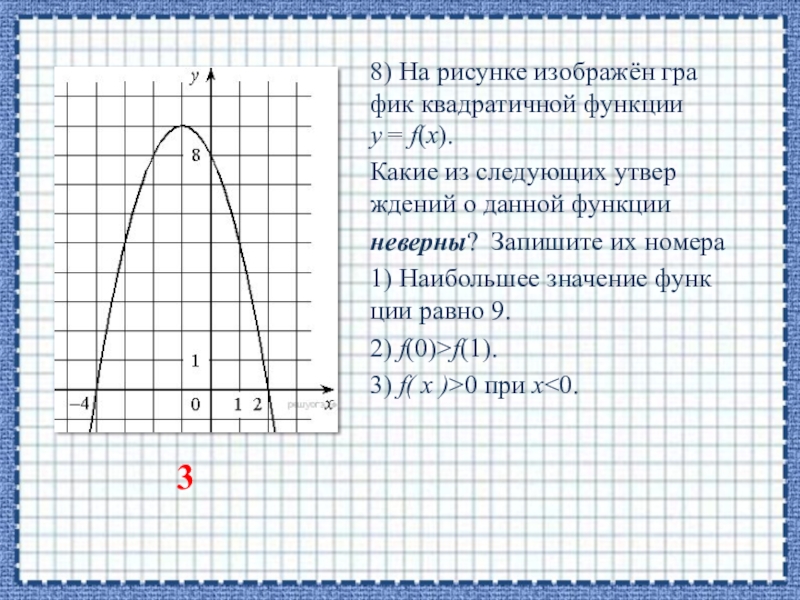
Слайд 168) На рисунке изображён график квадратичной функции y = f(x).
Какие из следующих утверждений
о данной функции
неверны? Запишите их номера
1) Наибольшее значение функции равно 9.
2) f(0)>f(1).
3) f( x )>0 при x<0.
неверны? Запишите их номера
1) Наибольшее значение функции равно 9.
2) f(0)>f(1).
3) f( x )>0 при x<0.
3
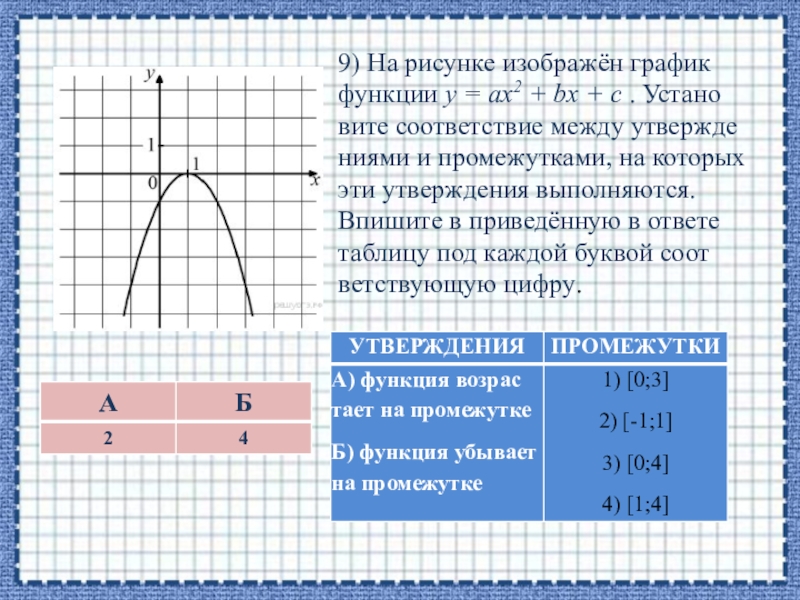
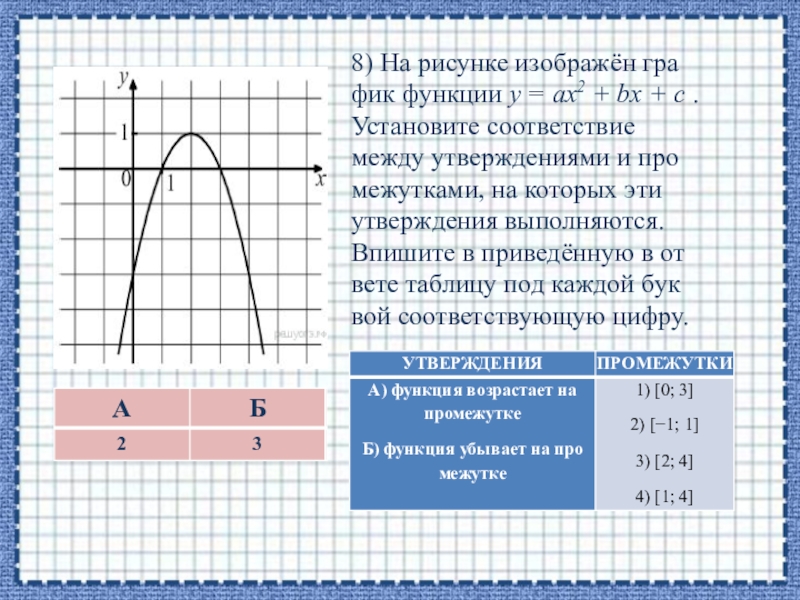
Слайд 179) На рисунке изображён график функции y = ax2 + bx
+ c . Установите соответствие между утверждениями и промежутками, на которых эти утверждения выполняются. Впишите в приведённую в ответе таблицу под каждой буквой соответствующую цифру.
Слайд 188) На рисунке изображён график функции y = ax2 + bx
+ c . Установите соответствие между утверждениями и промежутками, на которых эти утверждения выполняются. Впишите в приведённую в ответе таблицу под каждой буквой соответствующую цифру.
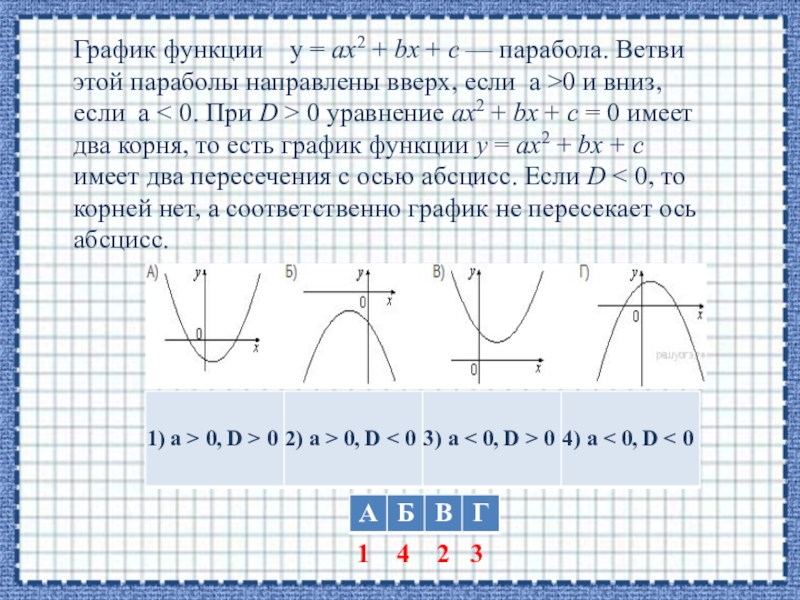
Слайд 199) На рисунке изображены графики функций вида y = ax2
+ bx + c. Для каждого графика укажите соответствующее ему значения коэффициента a и дискриминанта D. Графики
Знаки чисел
Запишите в ответ цифры, расположив их в порядке,
соответствующем буквам:
Слайд 20График функции у = ax2 + bx + c — парабола. Ветви этой параболы направлены
вверх, если а >0 и вниз, если а < 0. При D > 0 уравнение ax2 + bx + c = 0 имеет два корня, то есть график функции y = ax2 + bx + c имеет два пересечения с осью абсцисс. Если D < 0, то корней нет, а соответственно график не пересекает ось абсцисс.
1 4 2 3


![Презентация по математике на тему Чтение графиков функций Проверим каждое из утверждений.1) На луче (−∞; −1] большему значению аргумента Проверим каждое из утверждений.1) На луче (−∞; −1] большему значению аргумента соответствует большее значение функции. Следовательно, функция](/img/thumbs/7df89bf75a480d4db28c0a2060167fcf-800x.jpg)