- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Числовые последовательности (10 класс)
Содержание
- 1. Презентация по математике на тему Числовые последовательности (10 класс)
- 2. Цели урока:рассмотреть определение числовой последовательности, виды последовательностей.
- 3. Определение числовой последовательностиФункцию у=f(x), где х натуральное
- 4. Типы числовых последовательностей.1) Возрастающая последовательность – каждый ее член
- 5. Свойства числовых последовательностей
- 6. Примеры бесконечных числовых последовательностей1, 2, 3, 4,
- 7. Обозначают члены последовательности так а1; а2; а3;
- 8. Словесный способ.
- 9. Последовательность чисел Фибоначчи – 1,
- 10. Последовательность чисел ФибоначчиФиллотаксис (листорасположение)
- 11. Арифметическая прогрессия Числовую последовательность, каждый
- 12. Геометрическая прогрессия Числовую последовательность,
- 13. Развитие учения о прогрессиях Прогрессия (от
- 14. Найдите закономерности и покажите их с
- 15. Задача: найти формулу общего члена
- 16. Последовательности заданы формулами:an=(-1)nn2an=n4an=n+4an=-n-2an=2n-5an=3n-12. Укажите, какими числами
- 17. Итак, ответьте на вопросы:Дайте определение числовой последовательности.Какие
- 18. Укажите окрестность точки а радиуса r в
- 19. Окрестностью какой точки и какого радиуса является
- 20. Рассмотрим две последовательности:
- 21. Определение.
- 22. Чему равен предел данной последовательности?Вывод:Вывод:
- 23. Свойства1) Предел суммы равен сумме пределов
- 24. Спасибо за внимание!
Слайд 1Числовая последовательность. Способы задания последовательности. Предел числовой последовательности
10 класс
Методическая разработка учителя
Гурь-Арья Е.В.
Слайд 2Цели урока:
рассмотреть определение числовой последовательности, виды последовательностей. Примеры записей последовательностей.
рассмотреть понятие
развить навык вычисления пределов числовых последовательностей
1
2
3
Слайд 3Определение числовой последовательности
Функцию у=f(x), где х натуральное число называют функцией натурального
Слайд 4 Типы числовых последовательностей.
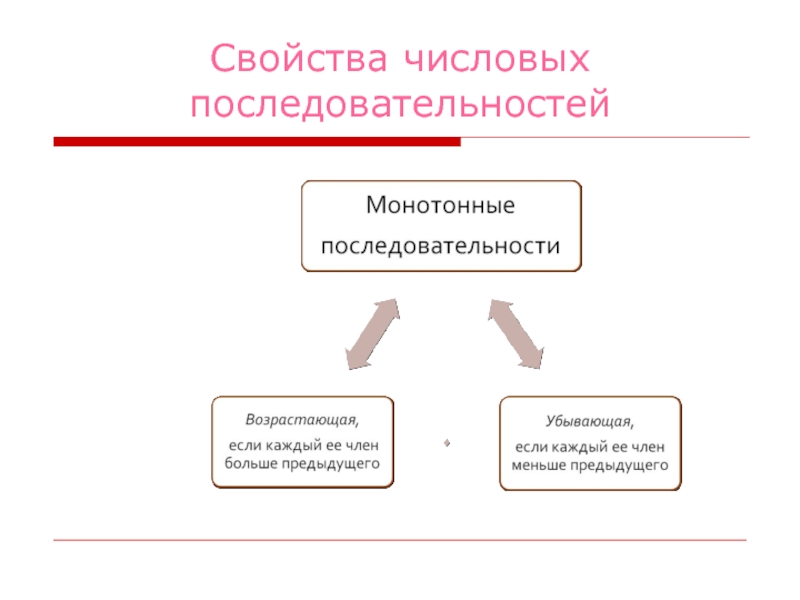
1) Возрастающая последовательность – каждый ее член больше предыдущего
2) Неубывающая последовательность –
3) Убывающая последовательность – каждый новый член меньше предыдущего
4) Невозрастающая последовательность – каждый старший член не больше предыдущего
5) Ограниченная последовательность имеет место тогда, когда найдутся такие действительные числа m и M , что для всех натуральных чисел выполняется неравенство
6) Последовательность называется неограниченной, если она постоянно или растет или убывает.
7) Последовательность, имеющая предел называется сходящейся. Противоположная к ней последовательность - соответственно расходящимися.
Слайд 6Примеры бесконечных числовых последовательностей
1, 2, 3, 4, 5, … - последовательность
2, 4, 6, 8, 10,… - последовательность чётных чисел.
1, 3, 5, 7, 9,… - последовательность нечётных чисел.
1, 4, 9, 16, 25,… - последовательность квадратов натуральных чисел.
2, 3, 5, 7, 11… - последовательность простых чисел.
Слайд 7Обозначают члены последовательности так
а1; а2; а3; а4; … аn
Способы
Аналитический. С помощью формулы n-ого члена – позволяет вычислить член последовательности с любым заданным номером
хn=3.n+2
x5=3.5+2=17;
Х45=3.45+2=137
Рекуррентный (от слова
recursio - возвращаться)
х1=1; хn+1=(n+1)xn
n=1; 2; 3; …
можно записать с многоточием
1; 2; 6; 24; 120; 720; …
Слайд 9Последовательность чисел Фибоначчи – 1, 1, 2, 3, 5, 8, 13,
можно задать рекуррентно:
Слайд 10Последовательность
чисел Фибоначчи
Филлотаксис (листорасположение) — правило, по которому располагаются,
Семечки упорядочены
в два ряда спиралей,
один из которых идет
по часовой стрелке,
другой против неё.
Слайд 11 Арифметическая прогрессия
Числовую последовательность, каждый член которой, начиная со
Пример: 1, 3, 5, 7, 9, 11, …
возрастающая арифметическая прогрессия,
у которой d = 2.
Слайд 12
Геометрическая прогрессия
Числовую последовательность, все члены которой отличны от нуля
q – знаменателем геометрической прогрессии.
Пример: 54 , 18, 6, 2, … -убывающая
геометрическая прогрессия,
у которой q = 1/3.
Слайд 13
Развитие учения о прогрессиях
Прогрессия (от латинского progressio) -«движение вперёд»
Наблюдая луну от
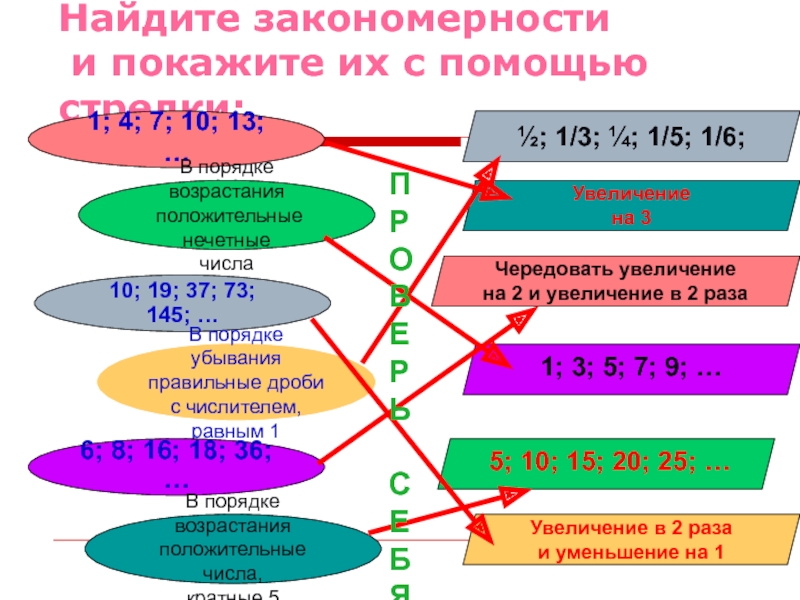
Слайд 14Найдите закономерности
и покажите их с помощью стрелки:
1; 4; 7; 10;
В порядке возрастания
положительные нечетные
числа
10; 19; 37; 73; 145; …
В порядке убывания
правильные дроби
с числителем, равным 1
6; 8; 16; 18; 36; …
В порядке возрастания
положительные числа,
кратные 5
½; 1/3; ¼; 1/5; 1/6;
Увеличение
на 3
Чередовать увеличение
на 2 и увеличение в 2 раза
1; 3; 5; 7; 9; …
5; 10; 15; 20; 25; …
Увеличение в 2 раза
и уменьшение на 1
П
Р
О
В
Е
Р
Ь
С
Е
Б
Я
Слайд 15
Задача: найти формулу общего члена последовательности:
6; 20; 56; 144; 352;…
Решение.
в следующем виде:
Формула общего члена:
Слайд 16 Последовательности заданы формулами:
an=(-1)nn2
an=n4
an=n+4
an=-n-2
an=2n-5
an=3n-1
2. Укажите, какими числами являются члены этих последовательностей
Положительные
Выполните следующие задания:
Впишите пропущенные члены последовательности:
1; ___; 81; ___; 625; … 5; ___; ___; ___; 9; … ___; ___; 3; 11; ___;
-1; 4; ___; ___; -25; … ___; -4 ; ___; ___; -7; …
2; 8; ___; ___; ___; …
16 256 6 7 8 -3 -1 27
-9 16 -3 -5 -6
26 80 242
ПРОВЕРЬ
СЕБЯ
Слайд 17Итак, ответьте на вопросы:
Дайте определение числовой последовательности.
Какие способы задания числовой последовательности
Дайте определение ограниченной сверху и снизу числовой последовательности.
Какую последовательность называют возрастающей и убывающей?
Что такое окрестность точки, радиус окрестности?
Слайд 18Укажите окрестность точки а радиуса r в виде интервала, если:
а) а
r = 0,1
b) a = -3
r = 0,5
в) а = 2
r = 1
г) а = 0,2
r = 0,3
(-0,1, 0,1)
(-3,5, -2,5)
(1, 3)
(-0,1, 0,5)
Слайд 19Окрестностью какой точки и какого радиуса является интервал
а) (1, 3)
б) (-0,2,
г) (-7, -5)
в) (2,1, 2,3)
а = 2
r = 1
а = 0
r = 0,2
а = 2,2
r = 0,1
а = -6
r = 1
Слайд 21Определение.
Число b называют пределом
Пишут и читают:
или
Слайд 23Свойства
1) Предел суммы равен сумме пределов
2) Предел произведения равен произведению пределов
4) Постоянный множитель можно вынести за знак предела
3) Предел частного равен частному от пределов