А.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Численные методы (11 класс)
Содержание
- 1. Презентация по математике на тему Численные методы (11 класс)
- 2. На прошлом уроке, мы с вами вычисляли
- 3. методы Метод прямоугольниковМетод трапеций
- 4. Определенный интеграл и его геометрический смыслПусть на
- 5. Определенный интегралФормула Ньютона-Лейбница
- 6. Слайд 6
- 7. Метод прямоугольниковРешение многих задач сводиться к вычислению
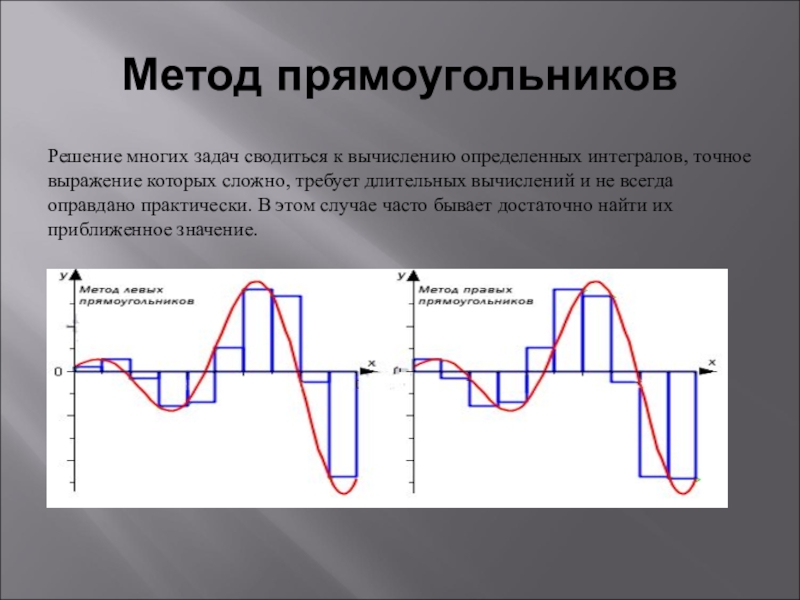
- 8. Метод прямоугольниковМетод левых прямоугольниковМетод правых прямоугольников
- 9. Метод прямоугольниковЧем больше n, тем точнее окончательный
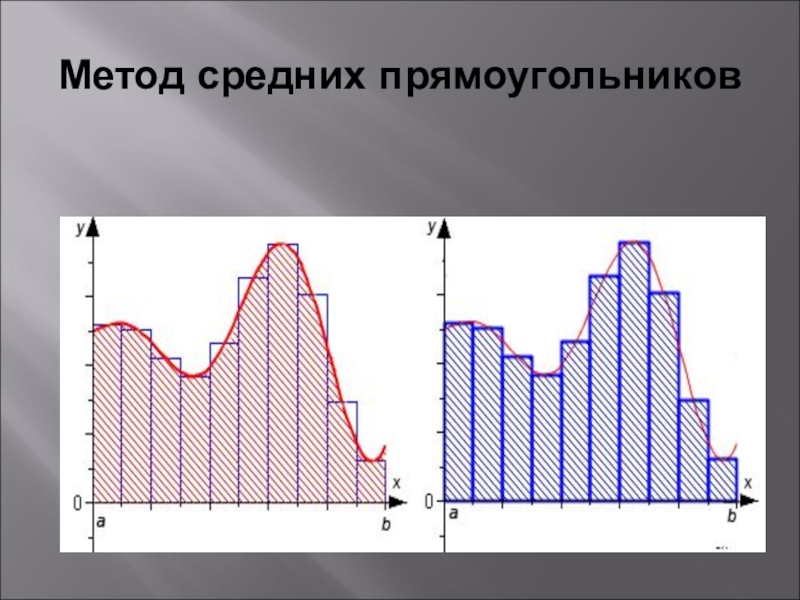
- 10. Метод средних прямоугольников
- 11. Метод средних прямоугольниковГде
- 12. Метод трапецийПлощадь криволинейной трапеции замениться суммой площадей
- 13. Метод трапеций
- 14. Метод трапеций
- 15. Домашнее заданиеОтветить на вопрос: 1. В чем
На прошлом уроке, мы с вами вычисляли определенные интегралы. Если функция задана аналитически и ее первообразная на этом отрезке может быть выражена в виде конечной комбинации элементарных функций, то для вычисления определенного интеграла используют формулу Ньютона-Лейбница.
Слайд 1Численные методы вычисления определенных интегралов
Учитель МБОУ СОШ №60
г. Чебоксары
Васильева Е.
Слайд 2На прошлом уроке, мы с вами вычисляли определенные интегралы. Если функция
задана аналитически и ее первообразная на этом отрезке может быть выражена в виде конечной комбинации элементарных функций, то для вычисления определенного интеграла используют формулу Ньютона-Лейбница. Если же функция задана аналитически, но ее первообразная не выражается в элементарных функциях, то значение определенного интеграла находят приближенными методами.
Слайд 4Определенный интеграл и его геометрический смысл
Пусть на отрезке [a, b] дана
непрерывная неотрицательная функция y=f(x). Проведем вертикальные прямые х=а, х=b до пересечения с графиком функции f(x).
Криволинейной трапецией называется фигура, ограниченная графиком непрерывной неотрицательной функции f(x), х [a, b], прямыми х=а, х=b и отрезком оси Ox.
Криволинейной трапецией называется фигура, ограниченная графиком непрерывной неотрицательной функции f(x), х [a, b], прямыми х=а, х=b и отрезком оси Ox.
Слайд 7Метод прямоугольников
Решение многих задач сводиться к вычислению определенных интегралов, точное выражение
которых сложно, требует длительных вычислений и не всегда оправдано практически. В этом случае часто бывает достаточно найти их приближенное значение.
Слайд 9Метод прямоугольников
Чем больше n, тем точнее окончательный результат, но вместе с
ростом n возрастает и объем вычислений.
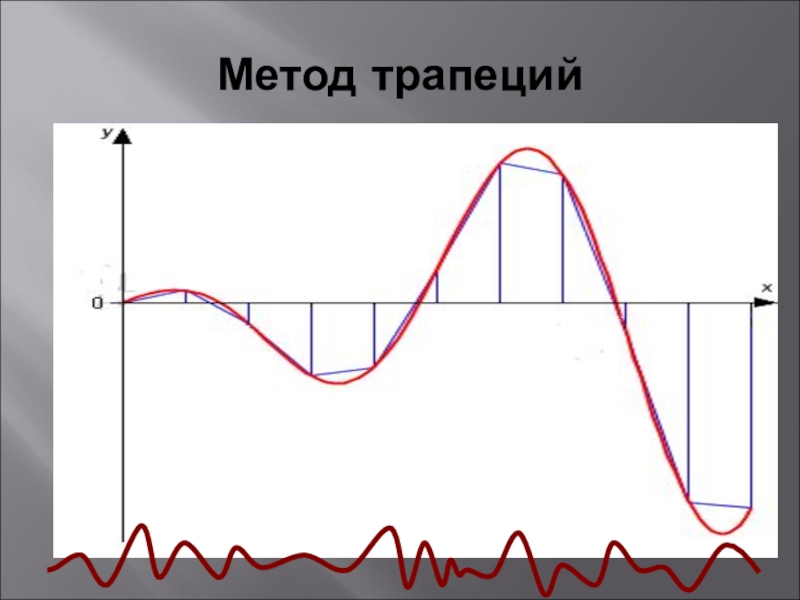
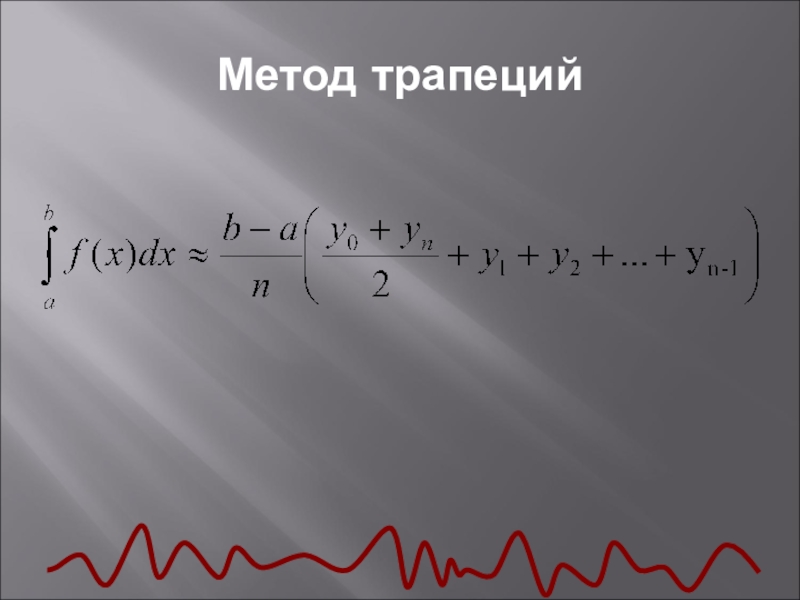
Слайд 12Метод трапеций
Площадь криволинейной трапеции замениться суммой площадей прямолинейных трапеций. Сумму площадей
всех элементарных трапеций можно принять за приближенное значение площади криволинейной трапеции, и за приближенное значение определенного интеграла.
С помощью приближенного интегрирования обычно находят интегралы, не поддающиеся точному вычислению. Однако мы ограничимся решением примеров, где точное значение интеграла находиться легко, для того чтобы сравнить полученное приближенное значение с точным
С помощью приближенного интегрирования обычно находят интегралы, не поддающиеся точному вычислению. Однако мы ограничимся решением примеров, где точное значение интеграла находиться легко, для того чтобы сравнить полученное приближенное значение с точным
Слайд 15Домашнее задание
Ответить на вопрос:
1. В чем заключается метод Симпсона для
вычисления определенного интеграла?
2. В чем отличие методов средних правых и левых прямоугольников?
2. В чем отличие методов средних правых и левых прямоугольников?


![Презентация по математике на тему Численные методы (11 класс) Определенный интеграл и его геометрический смыслПусть на отрезке [a, b] дана Определенный интеграл и его геометрический смыслПусть на отрезке [a, b] дана непрерывная неотрицательная функция y=f(x). Проведем вертикальные](/img/thumbs/636061ab89ab458c03eb5f1dd216ac5c-800x.jpg)