- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Арифметическая и геометрическая прогрессии(9 класс)
Содержание
- 1. Презентация по математике на тему Арифметическая и геометрическая прогрессии(9 класс)
- 2. Слайд 2
- 3. Герберт Спенсер, английский философ, когда-то сказал: "Дороги
- 4. Последовательность задана формулой yn=11-3*n. Найдите: у8; ук-1.
- 5. Формулы
- 6. 1. Последовательность (вn) – арифметическая прогрессия ,
- 7. Термин “прогрессия” был введен римским автором Боэцием
- 8. Конечно же, в Древнем мире не пользовались
- 9. Правило для нахождения суммы членов произвольной арифметической
- 10. Много в этой области работал знаменитый немецкий
- 11. Но, несмотря на пятидесяти вековую древность различных
- 12. Формулы
- 13. Решение задачЗадача 1В геометрической прогрессии b1=12,8 и
- 14. Задача 2Из данных последовательностей назовите арифметическую последовательность
- 15. Задача 2 Найдем восьмой член геометрической прогрессии
- 16. Задача 3Решение :10% = 0,1. Коэффициент увеличения
- 17. Уже в Древнем Египте знали не только
- 18. Слайд 18
- 19. В написанной в XIII в. «Книге об
- 20. Формулы
- 21. Пример. Обратим периодическую дробь 0,58(3) в обыкновенную.
- 22. Пример. Обратим периодическую дробь 0,58(3) в
- 23. Индийский царь Шерам призвал к себе изобретателя
- 24. на 1-ю 1, на 33-ю
- 25. Древняя индийская легенда Сколько зёрен должен был
- 26. 18 квинтиллионов 446 квадриллионов 744 триллиона 73 миллиарда(биллиона) 709 миллионов 551 тысяча 615
- 27. Современники сказали бы так:
- 28. Задача 1 . Найдите сумму
- 29. Задача 2 . Сумма первого и
- 30. "Прогрессио - движение вперёд!" Урок сегодня завершён,
- 31. Домашнее задание: Повторить п. №Подготов. к контрольной работе
- 32. Спсибо за урок. Желаю успехов !
Слайд 2
Образовательные: обобщить, расширить и углубить знания по применению свойств арифметической и геометрической прогрессии к решению задач;
проверить сформированность умений и навыков;
Развивающие: развить интерес учащихся к предмету, их стремление глубже усвоить предмет и навыки индивидуальной, групповой и коллективной работы;
Воспитательные: воспитывать чувства товарищества и взаимопомощи.
Слайд 3Герберт Спенсер, английский философ, когда-то сказал: "Дороги не те знания, которые
Слайд 61. Последовательность (вn) – арифметическая прогрессия , первый член которого равен
2. (аn )-арифметическая прогрессия, а1 =10; d = - 0,1. Найдиде а 4 .
Слайд 7Термин “прогрессия” был введен римским автором Боэцием еще в IV в.
Слайд 8Конечно же, в Древнем мире не пользовались нашими стандартными понятиями и
Слайд 9Правило для нахождения суммы членов произвольной арифметической прогрессии даётся в «Книге
А общее правило для суммирования любой конечной геометрической прогрессии встречается в книге Н. Шюке «Наука о числах», увидевшей свет в 1484 году.
Наука о числах
Слайд 10Много в этой области работал знаменитый немецкий математик К.Гаусс (1777 г.-1855г.)
Слайд 11Но, несмотря на пятидесяти вековую древность различных задач на прогрессии, в
В первом учебнике “Арифметика” Леонида Филипповича Магницкого, изданном двести лет назад и служившем целых полвека основным руководством для школьного обучения, прогрессии хотя и имеются, но общих формул, связывающих входящие в них величины между собою, в нем не дано. Поэтому сам составитель учебника не без затруднений справлялся с такими задачами.
Слайд 13Решение задач
Задача 1
В геометрической прогрессии b1=12,8 и q=1/4. Найдите b7.
Решение:
b7
Слайд 14Задача 2
Из данных последовательностей назовите арифметическую последовательность и указать разность и
2,12,22,32…
5,5,5,…
3. 1,3,9,27,…
4. 1,2,3,4,5….
5. -2,-6,-10,…
6. 2,4,8,16,…
Слайд 15Задача 2
Найдем восьмой член геометрической прогрессии (bn), если b1 =162
Решение :
используя формулу (*), найдем знаменатель q.
Так как b3=b1∙q2, то q2=b3 / b1=18 / 162=1/9.
Решив уравнение q2 = 1/9, получим q = ±1/3.
Таким образом, существуют две прогрессии, удовлетворяющие условию задачи.
Если q = 1/3, то b8 =b1∙q7=2/27.
Если q = -1/3, то b8 = -2/27.
Задача имеет два решения:
b8 = 2/27 и b8 = -2/27.
Слайд 16Задача 3
Решение :
10% = 0,1. Коэффициент увеличения вклада равен 1,1. Имеем
с1 = 1000 р., q = 1,1. с4 – вклад через три года. Следовательно,
с4 = с1 . q3 = 1000 . (1,1)3 = 1331.
Через три года вклад будет равен 1331 р.
Срочный вклад 1000 р., положенный в банк, ежегодно увеличивается на 10%. Каким станет вклад через 3 года?
Слайд 17Уже в Древнем Египте знали не только арифметическую, но и геометрическую
"В доме было 7 кошек.
Каждая кошка съедает 7 мышей.
Каждая мышь съедает 7 колосьев.
Каждый колос дает 7 растений.
На каждом растении вырастает 7 мер зерна.
Сколько всех вместе?".
Найдите ответ к этой задаче.
Слайд 18
кошек 72 = 49,
они съедают всего 73 = 343 мыши, которые
съедают всего 74 = 2401 колосьев, из них
вырастает 75 = 16807 мер ячменя,
в сумме эти числа дают 19 607.
Ответ: 19607.
Слайд 19
В написанной в XIII в. «Книге об абаке» Леонардо Пизанского (Фибоначчи)
Эта задача много раз с разными вариациями повторялась и у других народов в другие времена.
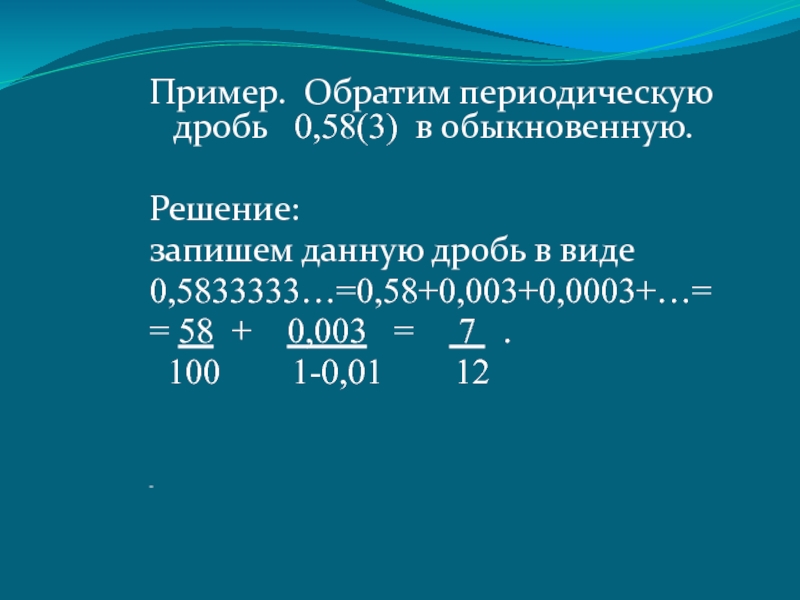
Слайд 22Пример. Обратим периодическую дробь 0,58(3) в обыкновенную.
Решение:
запишем данную дробь
0,5833333…=0,58+0,003+0,0003+…=
= 58 + 0,003 = 7 .
100 1-0,01 12
=
Слайд 23Индийский царь Шерам призвал к себе изобретателя шахмат (которого звали Сета)
Древняя индийская легенда
Слайд 24на 1-ю 1, на 33-ю
на 2-ю 2, на 34-ю 8 589 934 592
на 3-ю 4, на 35-ю 17 179 869 184
на 4-ю 8, на 36-ю 34 359 738 368
………………………………………………
на 62-ю 2 305 843 009 213 693 952
на 63-ю 4 611 686 018 427 387 904
на 64-ю 9 223 372 036 854 775 808
Слайд 25Древняя индийская легенда
Сколько зёрен должен был получить изобретатель шахмат?
S 64 = 2 - 1=
=18 446 744 073 704 551 615
64