11 классе (особенности решения заданий части В)
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике Методика подготовки к ГИА в 9 классе
Содержание
- 1. Презентация по математике Методика подготовки к ГИА в 9 классе
- 2. Основной целью единого государственного
- 3. Основной целью учителя , который готовит учащихся
- 4. ПРОБЛЕМЫ, ВОЗНИКШИЕ В СВЯЗИ С ИЗМЕНЕНИЕМ СТРУКТУРЫ
- 5. Распределение заданий В части работы по разделам
- 6. http://mathege.ruГлавная задача открытого банка заданий ЕГЭ по
- 7. Задания части ВСамостоятельные работыВарианты ЕГЭ Варианты заданий для обобщающего повторения
- 8. Задание В1.Это задание, моделирующее реальную или близкую
- 9. Типичные ошибки:Вычислительные (разучились считать без калькулятора)Не умение
- 10. Задачи, в которых было допущено наибольшее количество
- 11. ЗАДАНИЯ ЕГЭ 2013Система навигации, встроенная в спинку
- 12. Рост Джона 6 футов 1 дюйм. Выразите
- 13. Задание В2.Задание на чтение графика функции, моделирующее
- 14. Типичные ошибки:Невнимательность при чтении задания, вследствие чего
- 15. Задачи, в которых было допущено наибольшее количество
- 16. Задание В3.Задание на вычисления площади треугольника, четырехугольника,
- 17. ЗАДАНИЯ ЕГЭ 2013
- 18. ЗАДАНИЯ ЕГЭ 2013 Найдите квадрат длины вектора
- 19. Задание В4.Задание на анализ практической ситуации, несложная
- 20. Типичные ошибки:Неправильные ответы связаны в основном с
- 21. ЗАДАНИЯ ЕГЭ 2013
- 22. Задание В5.Это не сложное показательное, логарифмическое или
- 23. Типичные ошибки:Неправильные ответы связаны в основном с арифметическими ошибкамиОбратить внимание на логарифмические уравнения, требующие предварительных преобразований.
- 24. ЗАДАНИЯ ЕГЭ 2013Найдите корень уравнения .Найдите корень уравнения .
- 25. Задание В6.Задание на вычисление элементов прямоугольного треугольника,
- 26. ЗАДАНИЯ ЕГЭ 2012,2013Найдите радиус r окружности, вписанной в четырехугольник ABCD. В ответе укажите
- 27. ЗАДАНИЯ ЕГЭ 2012,2013Найдите радиус окружности, вписанной в
- 28. Задание В7.Задание на вычисление значения тригонометрического, логарифмического,
- 29. Типичные ошибки:Могут быть допущены в любом из заданий
- 30. Наиболее сложные задания:По тригонометрии: на применение формул
- 31. ЗАДАНИЯ ЕГЭ 2013Найдите значение выражения Найдите значение выражения
- 32. Задание В8.Задание основано на знании геометрического смысла
- 33. Типичные ошибки:По количеству допущенных ошибок задание является
- 34. Наиболее сложные задания:Таковыми оказались практически все задания.
- 35. ЗАДАНИЯ ЕГЭ 2012,2013
- 36. ЗАДАНИЯ ЕГЭ 2012,2013
- 37. ЗАДАНИЯ ЕГЭ 2013
- 38. ЗАДАНИЯ ЕГЭ 2013На рисунке изображён график некоторой
- 39. ЗАДАНИЯ ЕГЭ 2013На рисунке изображён график некоторой
- 40. ЗАДАНИЯ ЕГЭ 2013На рисунке изображён график функции
- 41. ЗАДАНИЯ ЕГЭ 2013Функция
- 42. Задание В10.Задание по теории вероятностей, связанное с
- 43. Типичные ошибки:В основном это либо вычислительные ошибки,
- 44. ЗАДАНИЯ ЕГЭ 2012В сборнике билетов по математике
- 45. ЗАДАНИЯ ЕГЭ 2013Автоматическая линия изготавливает батарейки. Вероятность
- 46. ЗАДАНИЯ ЕГЭ 2013Механические часы с двенадцатичасовым циферблатом
- 47. Задание В9 и В11.Задание на вычисление площадей
- 48. Задание В12.Текстовое задание, моделирующее реальную или близкую
- 49. Типичные ошибки:Задание не для слабого учащегося. Дети
- 50. Наиболее сложные задания:Очень сложно оказалось их выделить,
- 51. ЗАДАНИЯ ЕГЭ 2013
- 52. ЗАДАНИЯ ЕГЭ 2013
- 53. Задание В13.Кроме традиционных «текстовых» задач на движение
- 54. Типичные ошибки:Вычислительные ошибки (неумение извлекать квадратный корень
- 55. Наиболее сложные задания:Задачи на движение, в которых
- 56. ЗАДАНИЯ ЕГЭ 2012,2013
- 57. Задание В14.Задание на исследование функций с помощью
- 58. Типичные ошибки:Выбор корней тригонометрического уравнения. Неумение найти
- 59. Наиболее сложные задания:Задания на исследования логарифмической функцииЗадание
- 60. ЗАДАНИЯ ЕГЭ 2012,2013
- 61. Самостоятельные работыДолжны быть составлены минимум на 5
- 62. Задания ЕГЭ Закрепление материалаНатаскивание
- 63. Итоговое повторение.Составляется из заданий В части, с
- 64. Успешной сдачи экзаменов!
Основной целью единого государственного экзамена является объективная оценка уровня и качества подготовки выпускников общеобразовательных учреждений, на основе которой осуществляется итоговая аттестация выпускников и вступительные испытания в учреждения среднего и высшего профессионального образования.
Слайд 2 Основной целью единого государственного экзамена является объективная оценка
уровня и качества подготовки выпускников общеобразовательных учреждений, на основе которой осуществляется итоговая аттестация выпускников и вступительные испытания в учреждения среднего и высшего профессионального образования.
Слайд 3Основной целью учителя , который готовит учащихся к единому государственному экзамену
является: научить детей так, чтобы они все сдали этот экзамен (конечно будет значительно лучше, если они сдадут его хорошо).
Слайд 4ПРОБЛЕМЫ, ВОЗНИКШИЕ В СВЯЗИ С ИЗМЕНЕНИЕМ СТРУКТУРЫ БИЛЕТА ЕГЭ
Ежегодные изменения
в структуре экзаменационного билета
Постоянно меняющаяся база данных
Появление в базе данных новых, более сложных заданий
Проверка знания материала за курс всей средней школы
Отсутствие методических пособий, учитывающих эти изменения
Постоянно меняющаяся база данных
Появление в базе данных новых, более сложных заданий
Проверка знания материала за курс всей средней школы
Отсутствие методических пособий, учитывающих эти изменения
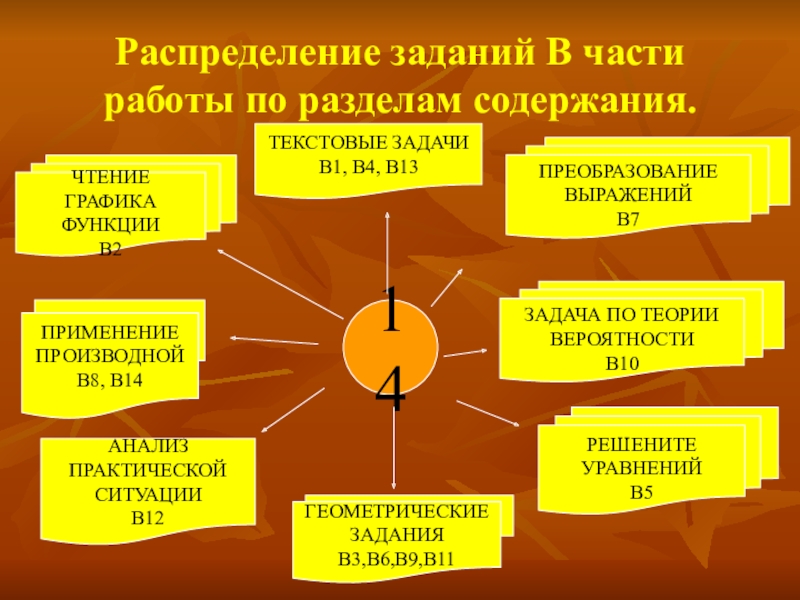
Слайд 5Распределение заданий В части работы по разделам содержания.
14
ЧТЕНИЕ ГРАФИКА
ФУНКЦИИ
В2
ТЕКСТОВЫЕ ЗАДАЧИ
В1,
В4, В13
ЗАДАЧА ПО ТЕОРИИ
ВЕРОЯТНОСТИ
В10
РЕШЕНИТЕ
УРАВНЕНИЙ
В5
ГЕОМЕТРИЧЕСКИЕ
ЗАДАНИЯ
В3,В6,В9,В11
АНАЛИЗ
ПРАКТИЧЕСКОЙ
СИТУАЦИИ
В12
ПРИМЕНЕНИЕ
ПРОИЗВОДНОЙ
В8, В14
ПРЕОБРАЗОВАНИЕ
ВЫРАЖЕНИЙ
В7
Слайд 6http://mathege.ru
Главная задача открытого банка заданий ЕГЭ по математике — дать представление
о том, какие задания будут в вариантах экзамена по математике в 2013 году, и помочь выпускникам сориентироваться при подготовке к экзамену.
Задачи открытого банка помогут будущим выпускникам повторить (освоить) школьный курс математики, найти в своих знаниях слабые места и ликвидировать их до экзамена. Задачи В1–В14 представлены заданиями, аналогичными экзаменационным (отличия — только в числовых параметрах).
Задачи открытого банка помогут будущим выпускникам повторить (освоить) школьный курс математики, найти в своих знаниях слабые места и ликвидировать их до экзамена. Задачи В1–В14 представлены заданиями, аналогичными экзаменационным (отличия — только в числовых параметрах).
Слайд 7Задания части В
Самостоятельные работы
Варианты ЕГЭ
Варианты заданий для обобщающего повторения
Слайд 8Задание В1.
Это задание, моделирующее реальную или близкую к реальной ситуацию. Для
решения задачи достаточно уметь выполнять арифметические действия, делать прикидку и оценку, знать понятие процента.
Слайд 9Типичные ошибки:
Вычислительные (разучились считать без калькулятора)
Не умение правильно ориентироваться в конкретных
практических ситуациях, часто решают задачу строго математически, не оценивая конкретную ситуацию.
Слайд 10Задачи, в которых было допущено наибольшее количество ошибок:
Задачи на проценты
Задачи на
округление ( с избытком или с недостатком)
Слайд 11ЗАДАНИЯ ЕГЭ 2013
Система навигации, встроенная в спинку самолетного кресла, информирует пассажира
о том, что полет проходит на высоте 37170 футов. Выразите высоту полета в метрах. Считайте, что 1 фут равен 30,5 см.
Бегун пробежал 50 м за 5 секунд. Найдите среднюю скорость бегуна на дистанции. Ответ дайте в километрах в час.
Бегун пробежал 50 м за 5 секунд. Найдите среднюю скорость бегуна на дистанции. Ответ дайте в километрах в час.
Слайд 12Рост Джона 6 футов 1 дюйм. Выразите рост Джона в сантиметрах,
если 1 фут равен 0,305 м, а 1 дюйм равен 2,54 см. Результат округлите до целого числа сантиметров.
Диагональ экрана телевизора равна 64 дюймам. Выразите диагональ экрана в сантиметрах, если в одном дюйме 2,54 см. Результат округлите до целого числа сантиметров.
Одна таблетка лекарства весит 20 мг и содержит 5% активного вещества. Ребёнку в возрасте до 6 месяцев врач прописывает 1,4 мг активного вещества на каждый килограмм веса в сутки. Сколько таблеток этого лекарства следует дать ребёнку весом в возрасте четырёх месяцев и весом 5 кг в течение суток
Диагональ экрана телевизора равна 64 дюймам. Выразите диагональ экрана в сантиметрах, если в одном дюйме 2,54 см. Результат округлите до целого числа сантиметров.
Одна таблетка лекарства весит 20 мг и содержит 5% активного вещества. Ребёнку в возрасте до 6 месяцев врач прописывает 1,4 мг активного вещества на каждый килограмм веса в сутки. Сколько таблеток этого лекарства следует дать ребёнку весом в возрасте четырёх месяцев и весом 5 кг в течение суток
Слайд 13Задание В2.
Задание на чтение графика функции, моделирующее реальную ситуацию или близкую
к реальной. График характеризует изменение в зависимости от времени некоторой величины ( температуры, стоимости акций и т.д.). Как правило , в задании требуется найти наибольшее (наименьшее) значение этой величины или разность между наибольшим и наименьшим значениями ( возможно за определенный период времени).
Слайд 14Типичные ошибки:
Невнимательность при чтении задания, вследствие чего отвечают не на поставленный
вопрос или неправильно воспринимают само задание.
Нахождение разности между наибольшим и наименьшим значениями, особенно при работе с отрицательными величинами.
Нахождение разности между наибольшим и наименьшим значениями, особенно при работе с отрицательными величинами.
Слайд 15Задачи, в которых было допущено наибольшее количество ошибок:
Задачи на определение разности
между наибольшим и наименьшим значениями
Задачи на нахождение наибольших и наименьших значений за определенный период
Задачи на нахождение наибольших и наименьших значений за определенный период
Слайд 16Задание В3.
Задание на вычисления площади треугольника, четырехугольника, круга и его частей,
в том числе по данным рисунка, представляющего собой изображение фигуры, площадь которой требуется найти, на клетчатой бумаге со стороной клетки равной 1.
Задание на нахождения суммы, разности, скалярного произведения векторов и угла между векторами.
Задание на нахождения суммы, разности, скалярного произведения векторов и угла между векторами.
Слайд 18ЗАДАНИЯ ЕГЭ 2013
Найдите квадрат длины вектора .
Стороны правильного треугольника
ABC равны 3. Найдите скалярное произведение векторов и .
Слайд 19Задание В4.
Задание на анализ практической ситуации, несложная текстовая задача (возможно с
табличными данными) на оптимальное решение, моделирующая реальную или близкую к реальной ситуацию.
Слайд 20Типичные ошибки:
Неправильные ответы связаны в основном с арифметическими ошибками
Неумение переводить из
одной системы единиц в другую (минуты в часы и записывать ответ в виде десятичной дроби)
Вместо выбора правильного ответа, указывают его наименование
Вместо выбора правильного ответа, указывают его наименование
Слайд 22Задание В5.
Это не сложное показательное, логарифмическое или иррациональное уравнение, которое сводится
в одно действие к линейному или квадратному (в этом случае в ответе нужно указать только один из корней меньший или больший)
Слайд 23Типичные ошибки:
Неправильные ответы связаны в основном с арифметическими ошибками
Обратить внимание на
логарифмические уравнения, требующие предварительных преобразований.
Слайд 25Задание В6.
Задание на вычисление элементов прямоугольного треугольника, связанные с определением тригонометрических
функций острых углов прямоугольного треугольника и задач, к ним приводимых, в том числе и по готовому чертежу.
Слайд 26ЗАДАНИЯ ЕГЭ 2012,2013
Найдите радиус r окружности, вписанной в четырехугольник ABCD. В
ответе укажите
Слайд 27ЗАДАНИЯ ЕГЭ 2012,2013
Найдите радиус окружности, вписанной в треугольник ABC, считая стороны
квадратных клеток равными 1.
Найдите радиус окружности, описанной около правильного треугольника ABC, считая стороны квадратных клеток равными 1.
Найдите радиус окружности, описанной около правильного треугольника ABC, считая стороны квадратных клеток равными 1.
Слайд 28Задание В7.
Задание на вычисление значения тригонометрического, логарифмического, иррационального выражения и выражения,
содержащего степени. Для решения данных заданий необходимо знать свойства логарифмов, степеней, уметь преобразовывать иррациональные и тригонометрические выражения.
Слайд 30Наиболее сложные задания:
По тригонометрии: на применение формул приведения и двойного угла
По
преобразованию иррациональных выражений: задания по преобразованию корней, степени которых различны
По преобразованию степенных выражений: умножение и деление степеней с разными основаниями
По преобразованию логарифмических выражений: задания, связанные с формулами перехода к новому основанию
По преобразованию степенных выражений: умножение и деление степеней с разными основаниями
По преобразованию логарифмических выражений: задания, связанные с формулами перехода к новому основанию
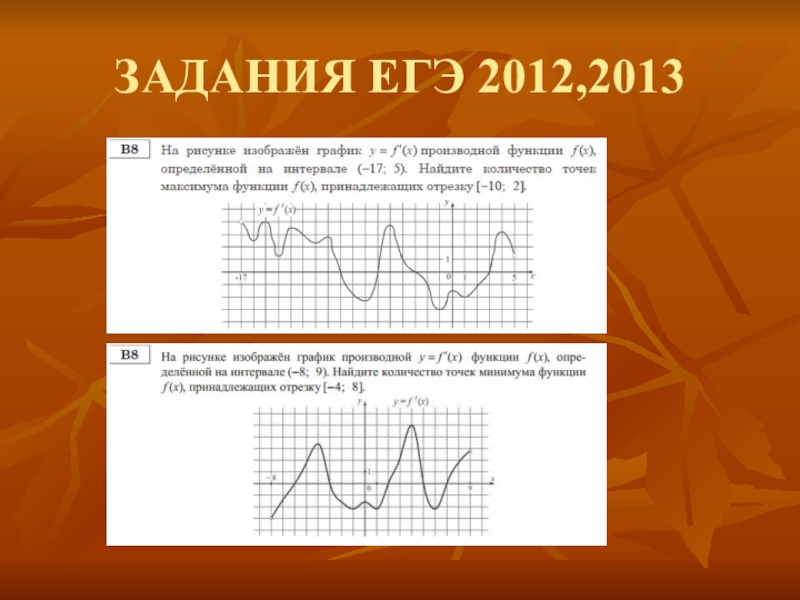
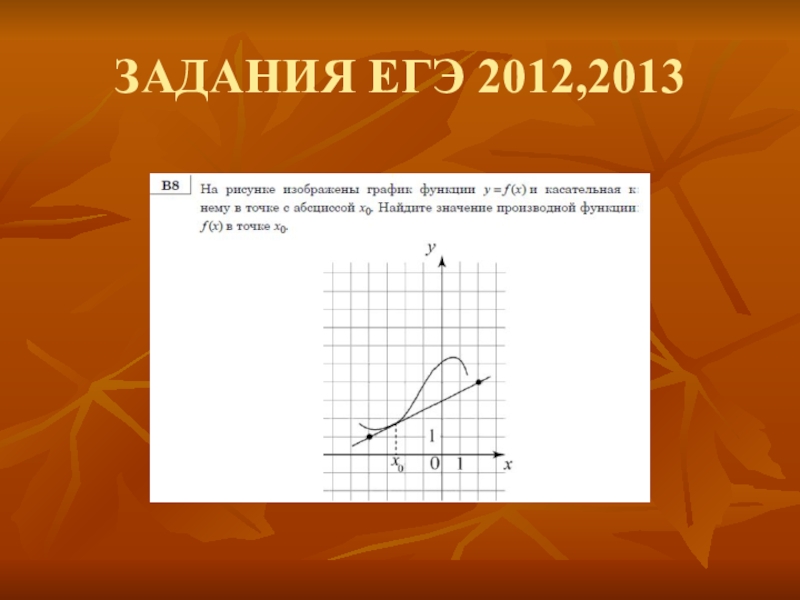
Слайд 32Задание В8.
Задание основано на знании геометрического смысла производной, это задание оказалось
наиболее сложным для понимания многими учащимися,
Умение вычислять площади фигур, первообразную и интеграл.
Умение вычислять площади фигур, первообразную и интеграл.
Слайд 33Типичные ошибки:
По количеству допущенных ошибок задание является рекордсменом
Неправильно определяют точки экстремума
по графику производной и по графику функции (часто путая эти графики из-за невнимательности)
Не видят, как себя ведет функция, если дан график ее производной
Забывают про геометрический смысл производной
Не видят, как себя ведет функция, если дан график ее производной
Забывают про геометрический смысл производной
Слайд 34Наиболее сложные задания:
Таковыми оказались практически все задания. С этими заданиями следует
начинать работать далеко не в 11 классе, а сразу после того, как пройдена тема «Геометрический смысл производной» и периодически повторять их
Определение по графику производной наибольшего или наименьшего значения функции
Определение количества точек, в которых касательная параллельна заданной прямой
Определение по графику производной наибольшего или наименьшего значения функции
Определение количества точек, в которых касательная параллельна заданной прямой
Слайд 38ЗАДАНИЯ ЕГЭ 2013
На рисунке изображён график некоторой функции
Функция — одна из первообразных функции . Найдите площадь закрашенной фигуры.
Слайд 39ЗАДАНИЯ ЕГЭ 2013
На рисунке изображён график некоторой функции
(два луча с общей начальной точкой). Пользуясь рисунком, вычислите , где — одна из первообразных функции .
Слайд 40ЗАДАНИЯ ЕГЭ 2013
На рисунке изображён график функции —
одной из первообразных некоторой функции , определённой на интервале . Пользуясь рисунком, определите количество решений уравнения на отрезке .
Слайд 41ЗАДАНИЯ ЕГЭ 2013
Функция
— одна из первообразных функции . Найдите площадь закрашенной фигуры.
Слайд 42Задание В10.
Задание по теории вероятностей, связанное с вычислением вероятности какого-либо события,
с 2013 года значительно увеличился объем задач в этом блоке и изменился так же и их уровень, став более сложным.
Слайд 43Типичные ошибки:
В основном это либо вычислительные ошибки, либо ошибки из-за невнимательности
В
этом году количество ошибок в данном задании может резко увеличиться, т.к. значительно усложнились сами задания.
Слайд 44ЗАДАНИЯ ЕГЭ 2012
В сборнике билетов по математике всего 25 билетов, в
10 из них встречается вопрос по неравенствам. Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику не достанется вопроса по неравенствам
В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 8 очков. Результат округлите до сотых.
В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 8 очков. Результат округлите до сотых.
Слайд 45ЗАДАНИЯ ЕГЭ 2013
Автоматическая линия изготавливает батарейки. Вероятность того, что готовая батарейка
неисправна, равна 0,02. Перед упаковкой каждая батарейка проходит систему контроля. Вероятность того, что система забракует неисправную батарейку, равна 0,99. Вероятность того, что система по ошибке забракует исправную батарейку, равна 0,01. Найдите вероятность того, что случайно выбранная из упаковки батарейка будет забракована.
Слайд 46ЗАДАНИЯ ЕГЭ 2013
Механические часы с двенадцатичасовым циферблатом в какой-то момент сломались
и перестали ходить. Найдите вероятность того, что часовая стрелка застыла, достигнув отметки 10, но не дойдя до отметки 1 час.
Слайд 47Задание В9 и В11.
Задание на вычисление площадей поверхностей или объемов многогранников
и тел вращения. Это задание на применение основных формул, связанных с вычислением площадей поверхностей или объемов многогранников (пирамид и призм) или тел вращения (цилиндров, конусов, шаров), в том числе вписанных или описанных около других многогранников или тел вращения.
Слайд 48Задание В12.
Текстовое задание, моделирующее реальную или близкую к реальной ситуацию (
например, физические, химические и др.процессы). Анализируя данную ситуацию, необходимо составить квадратное уравнение или неравенство.
Слайд 49Типичные ошибки:
Задание не для слабого учащегося. Дети не умеющие мыслить, не
могут по описанию практической ситуации построить ее математическую модель в виде квадратного неравенства или квадратного уравнения
Невнимательно читается само задание, в следствии чего учащийся даже не приступает к его решению, а часто достаточно просто подставив в уже данную в задаче формулу все известные в задаче величины получить ответ
Вычислительные ошибки
Невнимательно читается само задание, в следствии чего учащийся даже не приступает к его решению, а часто достаточно просто подставив в уже данную в задаче формулу все известные в задаче величины получить ответ
Вычислительные ошибки
Слайд 50Наиболее сложные задания:
Очень сложно оказалось их выделить, требуется кропотливая работа по
их прорешиванию, которую необходимо начинать, как только пройдены темы : «Решение квадратных неравенств» и «Степени», при этом неплохо подключить к решению этих задач учителей физики.
Слайд 53Задание В13.
Кроме традиционных «текстовых» задач на движение или работу, т.е. задач
на составление уравнения, которое сводится или к квадратному или к линейному, задачи на смеси, задачи на арифметическую и геометрическую прогрессии, а так же задачи на «сложные проценты»
Слайд 54Типичные ошибки:
Вычислительные ошибки (неумение извлекать квадратный корень из числа, не используя
калькулятор)
Неправильно составляют уравнения, особенно в задачах на производительность и движение по течению и против течения
Не умеют применять формулы арифметической и геометрической прогрессии к решению задач.
Не умеют решать задачи на сплавы и смеси.
Неправильно составляют уравнения, особенно в задачах на производительность и движение по течению и против течения
Не умеют применять формулы арифметической и геометрической прогрессии к решению задач.
Не умеют решать задачи на сплавы и смеси.
Слайд 55Наиболее сложные задания:
Задачи на движение, в которых весь путь принимается за
1
Задачи на совместную работу
Задачи на производительность
Задачи на проценты
Задачи на совместную работу
Задачи на производительность
Задачи на проценты
Слайд 57Задание В14.
Задание на исследование функций с помощью производной. В этом задании
с помощью производной необходимо вычислить значения точек экстремума данной функции или наибольшего (наименьшего) значения данной функции на данном отрезке.
Слайд 58Типичные ошибки:
Выбор корней тригонометрического уравнения. Неумение найти корни тригонометрического уравнения, принадлежащие
определенному промежутку.
Нахождение производной сложной функции
Не выполняют равносильные преобразования, которые упрощают дальнейшие исследования функции
Нахождение производной сложной функции
Не выполняют равносильные преобразования, которые упрощают дальнейшие исследования функции
Слайд 59Наиболее сложные задания:
Задания на исследования логарифмической функции
Задание на исследование функции у=tgx.
Исследование функций, содержащих корни и степени с дробным показателем.
Слайд 61Самостоятельные работы
Должны быть составлены минимум на 5 вариантов
Предусмотрены индивидуальные работы, с
учетом ошибок каждого учащегося
Варианты работ должны быть вариативными, в зависимости от того, как составлены задания они могут использоваться на различных этапах обучения (начиная с 5 класса)
Варианты работ должны быть вариативными, в зависимости от того, как составлены задания они могут использоваться на различных этапах обучения (начиная с 5 класса)
Слайд 63Итоговое повторение.
Составляется из заданий В части, с учетом наиболее типичных ошибок
Может проводиться, как в конце учебного года, так и непосредственно на консультациях перед экзаменом
Может для разных классов содержать различные задания