- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике Метод следов
Содержание
- 1. Презентация по математике Метод следов
- 2. Метод следов След- линия пересечения секущей плоскости с
- 3. Алгоритм построения следа секущей плоскости1. Находим проекции
- 4. Пример 1 На рёбрах ВВ1, СС1,
- 5. Пример1XY-искомый след
- 6. Пример2 На ребре МС пирамиды МАВСD задана
- 7. Пример2XY-искомый след.
- 8. Пример 3Построить сечение пирамиды DАВС плоскостью, проходящей
- 9. Пример3MNPK- искомое сечение
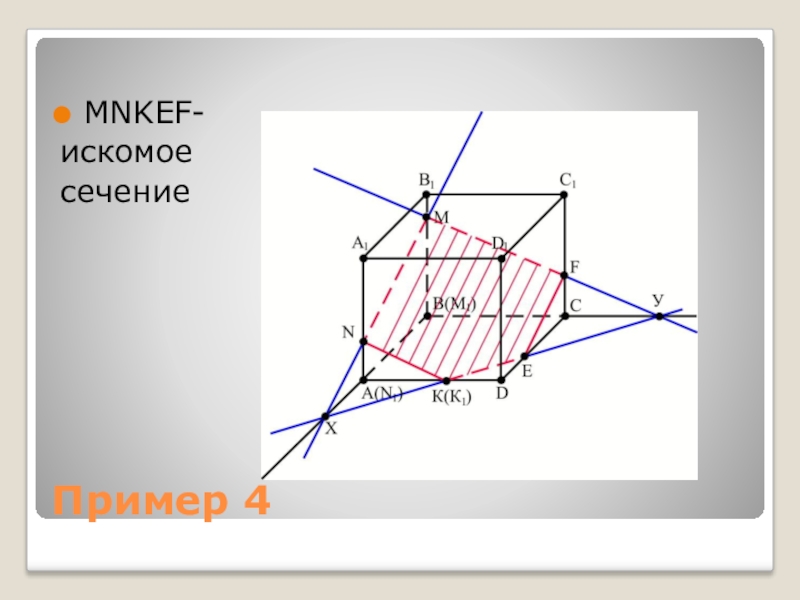
- 10. Пример 4Построить сечение параллелепипеда АВСDА1В1С1D1 плоскостью, проходящей
- 11. Пример 4MNKEF-искомое сечение
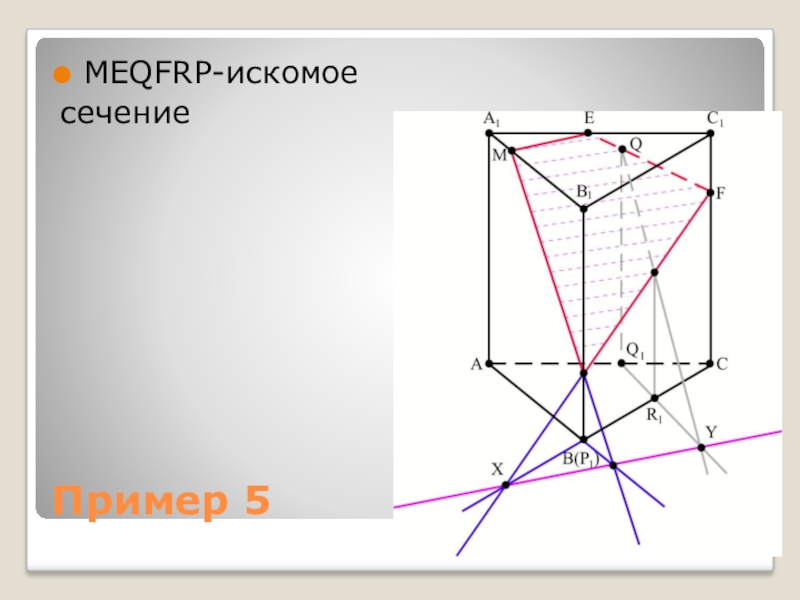
- 12. Пример 5 Построить сечение треугольной призмы плоскостью,
- 13. Пример 5 MEQFRP-искомое сечение
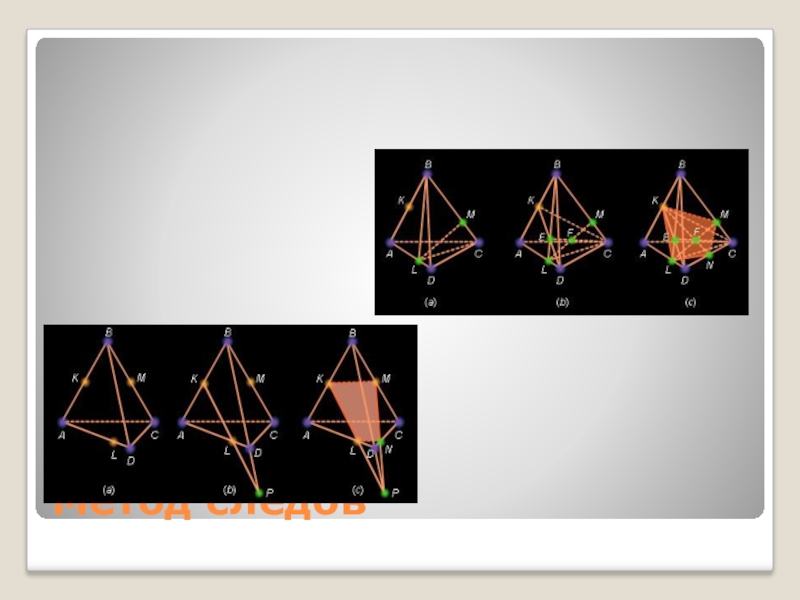
Метод следов След- линия пересечения секущей плоскости с каждой гранью многоугольника. След секущей плоскости будем находить на нижнем основании.
Слайд 2Метод следов
След- линия пересечения секущей плоскости с каждой гранью многоугольника. След
секущей плоскости будем находить на нижнем основании.
Слайд 3Алгоритм построения следа секущей плоскости
1. Находим проекции данных точек на плоскость
нижнего основания.
2.Строим точку X.
3. Строим точку Y.
4. XY – это след секущей плоскости на плоскость нижнего основания.
2.Строим точку X.
3. Строим точку Y.
4. XY – это след секущей плоскости на плоскость нижнего основания.
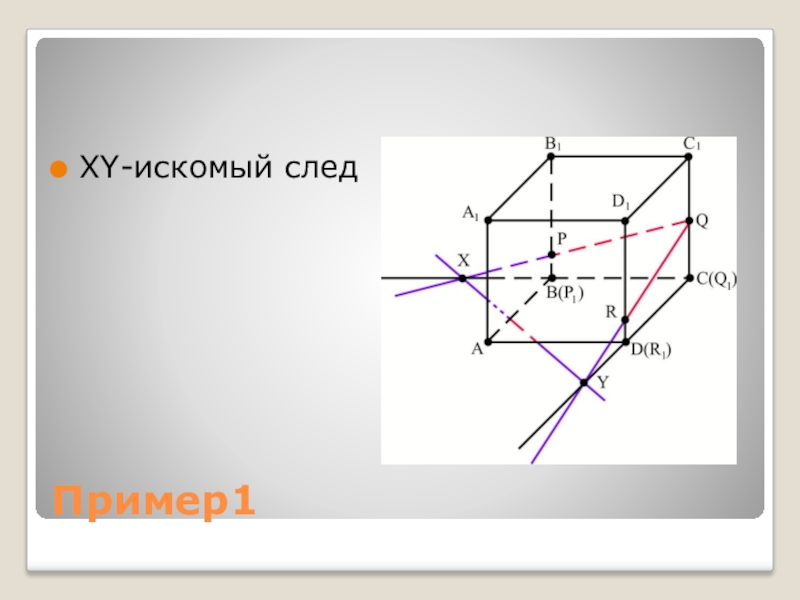
Слайд 4Пример 1
На рёбрах ВВ1, СС1, DD1 призмы АВСDА1В1С1D1 заданы
соответственно точки Р, Q и R. Построить основной след секущей плоскости PQR
РЕШЕНИЕ.
1) Найдём проекции точек P, Q, R на плоскость нижнего основания. Получим P1, Q1, R1.
2) Прямая РР1 ⎮⎮ QQ1, поэтому P, Q, P1, Q1 лежат в одной плоскости.
3) Построим точку Х – точку пересечения прямых PQ, и P1Q1.
4) Построим точку Y – точку пересечения прямых QR и Q1R1.
5) XY – искомый след.
РЕШЕНИЕ.
1) Найдём проекции точек P, Q, R на плоскость нижнего основания. Получим P1, Q1, R1.
2) Прямая РР1 ⎮⎮ QQ1, поэтому P, Q, P1, Q1 лежат в одной плоскости.
3) Построим точку Х – точку пересечения прямых PQ, и P1Q1.
4) Построим точку Y – точку пересечения прямых QR и Q1R1.
5) XY – искомый след.
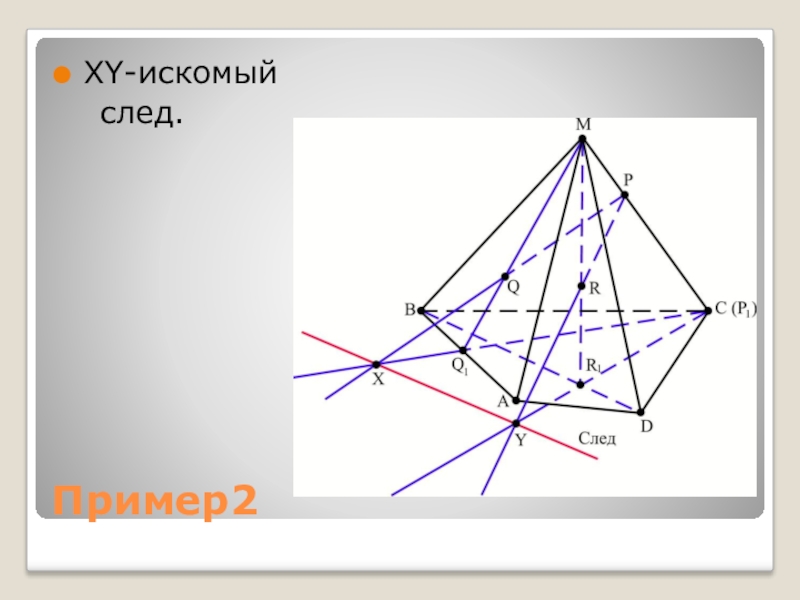
Слайд 6Пример2
На ребре МС пирамиды МАВСD задана точка Р, в грани
МАВ – точка Q, а внутри пирамиды в плоскости МВD – точка R. Построить основной след секущей плоскости PQR.
РЕШЕНИЕ
1) Найдём проекции точек P, Q, R на плоскость АВС, приняв вершину М за центр проектирования, получим точки P1, Q1, R1.
2) Построим точку Х – точку пересечения PQ, и P1Q1.
3) Построим точку Y – точку пересечения прямых РR и Р1R1.
4) XY – искомый след.
РЕШЕНИЕ
1) Найдём проекции точек P, Q, R на плоскость АВС, приняв вершину М за центр проектирования, получим точки P1, Q1, R1.
2) Построим точку Х – точку пересечения PQ, и P1Q1.
3) Построим точку Y – точку пересечения прямых РR и Р1R1.
4) XY – искомый след.
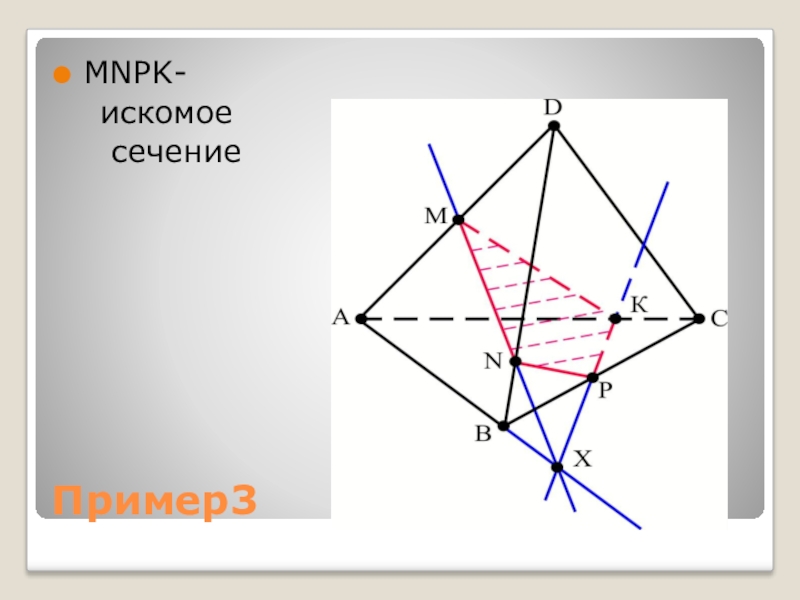
Слайд 8Пример 3
Построить сечение пирамиды DАВС плоскостью, проходящей через точки М, N,
P.
РЕШЕНИЕ.
1) Соединим точки М и N.
2) Соединим N и P.
3) Х – точка пересечения MN и АВ.
4) Через точки Х и P проведём прямую, которая пересечёт плоскость АВС в точке К.
5) Соединим точки М и К.
6) MNPK – искомое сечение.
РЕШЕНИЕ.
1) Соединим точки М и N.
2) Соединим N и P.
3) Х – точка пересечения MN и АВ.
4) Через точки Х и P проведём прямую, которая пересечёт плоскость АВС в точке К.
5) Соединим точки М и К.
6) MNPK – искомое сечение.
Слайд 10Пример 4
Построить сечение параллелепипеда АВСDА1В1С1D1 плоскостью, проходящей через точки М, К,
N.
РЕШЕНИЕ
1) Соединим точки M и N, N и K.
2) Найдём проекции точек M, N, K на плоскость АВСD, получим точки M1, N1, K1.
3) Х – точка пересечения MN и M1N1.
4) Y – точка пересечения ХК и ВY.
5) F – точка пересечения MY и ХY.
MNKEF-искомое сечение.
РЕШЕНИЕ
1) Соединим точки M и N, N и K.
2) Найдём проекции точек M, N, K на плоскость АВСD, получим точки M1, N1, K1.
3) Х – точка пересечения MN и M1N1.
4) Y – точка пересечения ХК и ВY.
5) F – точка пересечения MY и ХY.
MNKEF-искомое сечение.
Слайд 12Пример 5
Построить сечение треугольной призмы плоскостью, проходящей через точки P,
Q, R. P∈ВВ1, R∈(ВВ1С1С), Q∈(АА1С1С).
РЕШЕНИЕ
1) Построим проекции точек P, Q, R на плоскость нижнего основания. Получим P1, Q1, R1.
2) Х – точка пересечения РR и Р1R1.
3) Y – точка пересечения QR и Q1R1.
4) XY – след секущей плоскости.
5) Продолжим прямую АВ, получим точку, которую соединим с P и продолжим прямую. Она пересечёт А1В1 в точке М.
6) Соединим М и Е.
7) МЕQFRP – искомое сечение.
РЕШЕНИЕ
1) Построим проекции точек P, Q, R на плоскость нижнего основания. Получим P1, Q1, R1.
2) Х – точка пересечения РR и Р1R1.
3) Y – точка пересечения QR и Q1R1.
4) XY – след секущей плоскости.
5) Продолжим прямую АВ, получим точку, которую соединим с P и продолжим прямую. Она пересечёт А1В1 в точке М.
6) Соединим М и Е.
7) МЕQFRP – искомое сечение.