- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике к уроку по теме Теорема Виета.
Содержание
- 1. Презентация по математике к уроку по теме Теорема Виета.
- 2. «Лучший способ изучить что-либо - это открыть самому»Джордж Пойа
- 3. Вопросы Какое уравнение называют:1) квадратным 2) неполным3) приведённым.
- 4. Выписать в две строчки номера уравнений 1)
- 5. Взаимопроверка полные квадратные2; 4 приведённые1; 7; 8; 9
- 6. Физкультминутка
- 7. Слайд 7
- 8. Слайд 8
- 9. Слайд 9
- 10. Теорема ВиетаСумма корней приведенного квадратного уравнения равна
- 11. Теорема обратная теореме ВиетаЕсли m и n
- 12. Общая схема решения квадратных уравнений по теореме
- 13. Для уравнений вида ax2 + bx +
- 14. Франсуа Виет 1540 г. –
- 15. Примените т. Виета1.Составьте квадратное уравнение в котором
- 16. ВЗАИМОПРОВЕРКА 1)х2 + 5х +
- 17. Примените т. Виета1.Составьте квадратное уравнение в котором
- 18. 1)х2 -9х + 20 = 0
- 19. Домашнее заданиеПункт 24, № 580 бежз, 581
- 20. Слайд 20
- 21. Слайд 21
«Лучший способ изучить что-либо - это открыть самому»Джордж Пойа
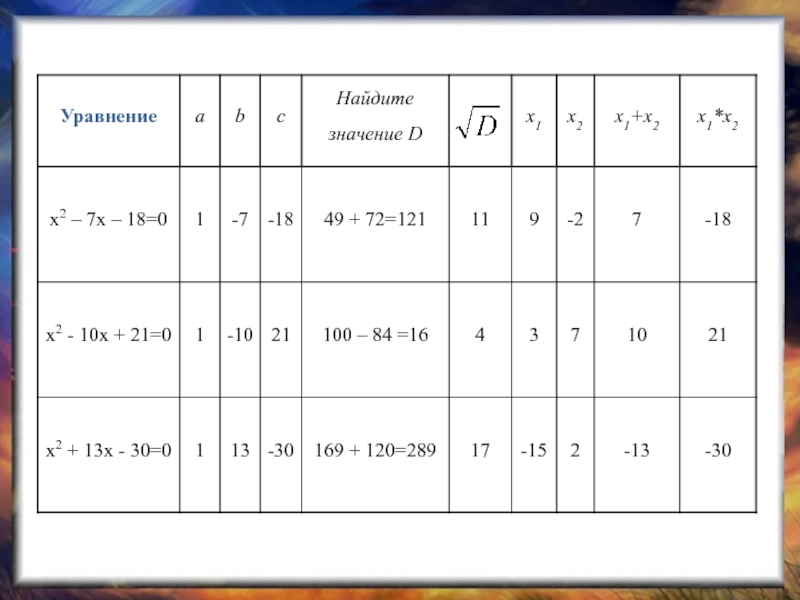
Слайд 4Выписать в две строчки номера уравнений 1) полные квадратные
2) приведённые
1)
х2 – 5х + 6 = 0
2) 3х2 – 5х +19 = 0
3) 7х2 – 14 = 0
4) 6х2 + 11х + 24 = 0
5) 2х2 + 6х = 6
6) х 2– 13х = 0
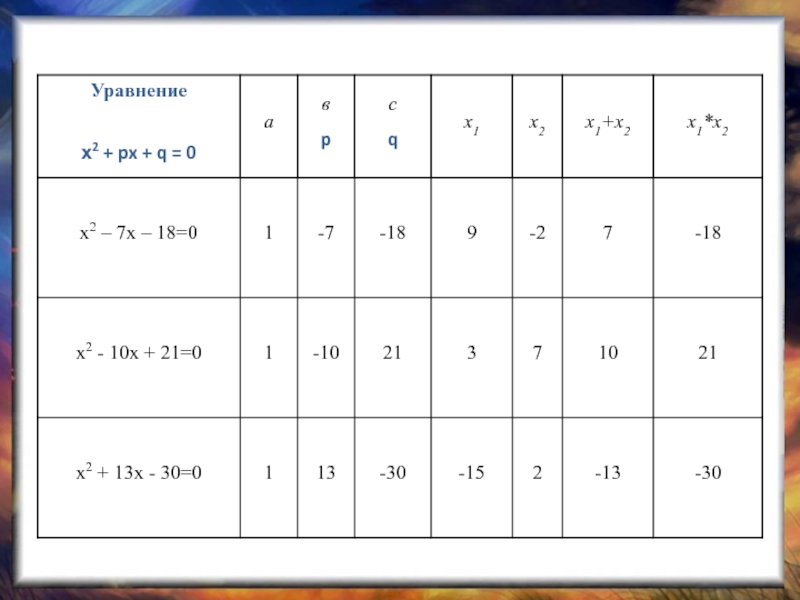
7) х2 – 7х - 18 = 0
2) 3х2 – 5х +19 = 0
3) 7х2 – 14 = 0
4) 6х2 + 11х + 24 = 0
5) 2х2 + 6х = 6
6) х 2– 13х = 0
7) х2 – 7х - 18 = 0
8) х2 – 10х + 21 = 0
9) х2 + 13х – 30 = 0
Слайд 10Теорема Виета
Сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с
противоположным знаком, а произведение корней равно свободному члену
х2 + px + q = 0
x1 + x2 = - p
x1 * x2 = q
Слайд 11Теорема обратная теореме Виета
Если m и n таковы, что их сумма
равна -p, а произведение равно q, то эти числа являются корнями уравнения х2 + px + q = 0.
m + n = - p
m* n = q
Слайд 12Общая схема решения квадратных уравнений по теореме Виета выглядит следующим образом:
привести
квадратное уравнение к приведенному, если это еще не сделано в условии задачи;
если коэффициенты в приведенном квадратном уравнении получились дробными, решаем через дискриминант;
в случае с целочисленными коэффициентами решаем уравнение по теореме Виета.
если коэффициенты в приведенном квадратном уравнении получились дробными, решаем через дискриминант;
в случае с целочисленными коэффициентами решаем уравнение по теореме Виета.
Слайд 13Для уравнений вида ax2 + bx + c= 0
x2 +
x + = 0
сумма корней равна х1 + х2 = - ,
а произведение х1 * х2 =
сумма корней равна х1 + х2 = - ,
а произведение х1 * х2 =
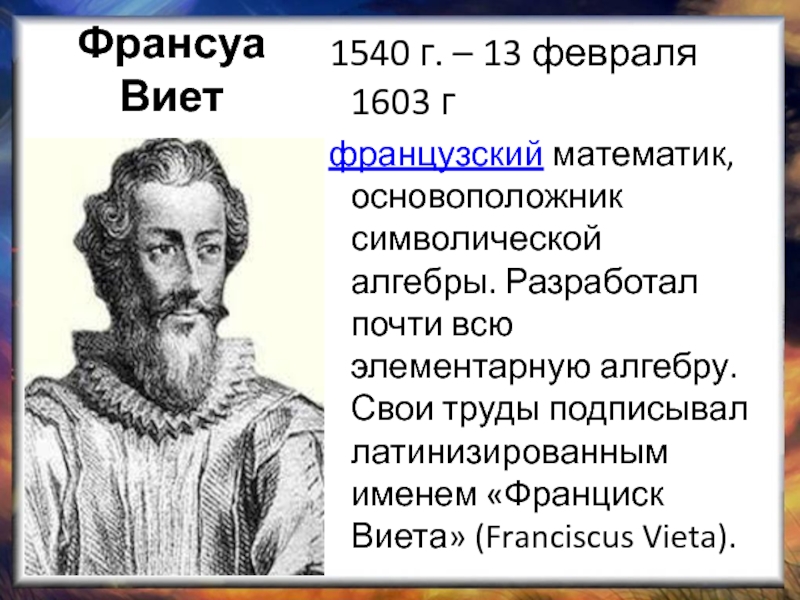
Слайд 14Франсуа Виет
1540 г. – 13 февраля 1603 г
французский математик,
основоположник символической алгебры. Разработал почти всю элементарную алгебру. Свои труды подписывал латинизированным именем «Франциск Виета» (Franciscus Vieta).
Слайд 15Примените т. Виета
1.Составьте квадратное уравнение в котором сумма p и произведение
q его корней равны:
а)p = 5; q = 6 б)p = 2; q = -3 в) p = 0; q = 6
2. Составьте квадратные уравнения по известному значению их корней:а)х1 =4;х2=-2 б)х1 =0;х2 =-5
а)p = 5; q = 6 б)p = 2; q = -3 в) p = 0; q = 6
2. Составьте квадратные уравнения по известному значению их корней:а)х1 =4;х2=-2 б)х1 =0;х2 =-5
Слайд 17Примените т. Виета
1.Составьте квадратное уравнение в котором сумма p и произведение
q его корней равны:
а)p = 9; q = 20 б)p =- 7; q = 0 в) p = 0; q = 4
2. Составьте квадратные уравнения по известному значению их корней:а)х1=-4;х2=-5 б)х1 =0;х2 =4
а)p = 9; q = 20 б)p =- 7; q = 0 в) p = 0; q = 4
2. Составьте квадратные уравнения по известному значению их корней:а)х1=-4;х2=-5 б)х1 =0;х2 =4
Слайд 19Домашнее задание
Пункт 24,
№ 580 бежз, 581 г, 583 б.
3. Решить
уравнение: х2 + 2013х – 2014 = 0