- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике и литературе на тему Математика в искусстве
Содержание
- 1. Презентация по математике и литературе на тему Математика в искусстве
- 2. Слайд 2
- 3. Гипотеза:математика как наука имеет свои
- 4. Задачи:познакомиться с новыми математическими понятиями (золотой
- 5. Геометрия владеет двумя сокровищами.
- 6. Золотое сечение. Золотым сечением
- 7. Ряд Фибоначчи. Месяцы 0
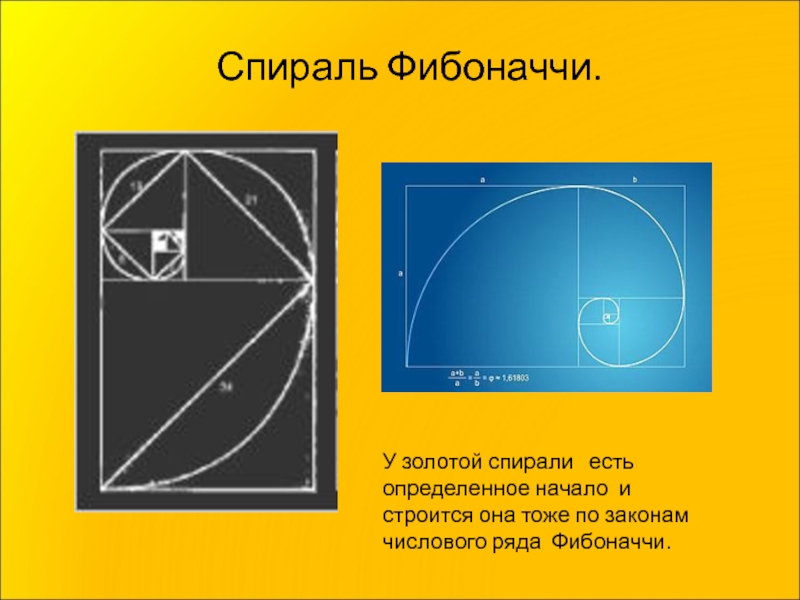
- 8. Спираль Фибоначчи.У золотой спирали есть определенное
- 9. Золотой прямоугольник. Отношение смежных сторон
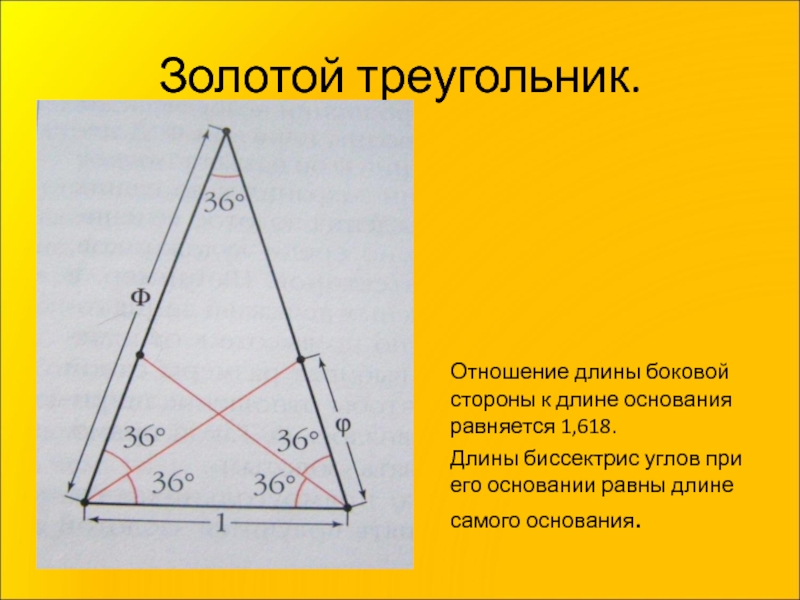
- 10. Золотой треугольник. Отношение длины боковой
- 11. Звёздчатый пятиугольник.Каждая из пяти линий, составляющая звездчатый
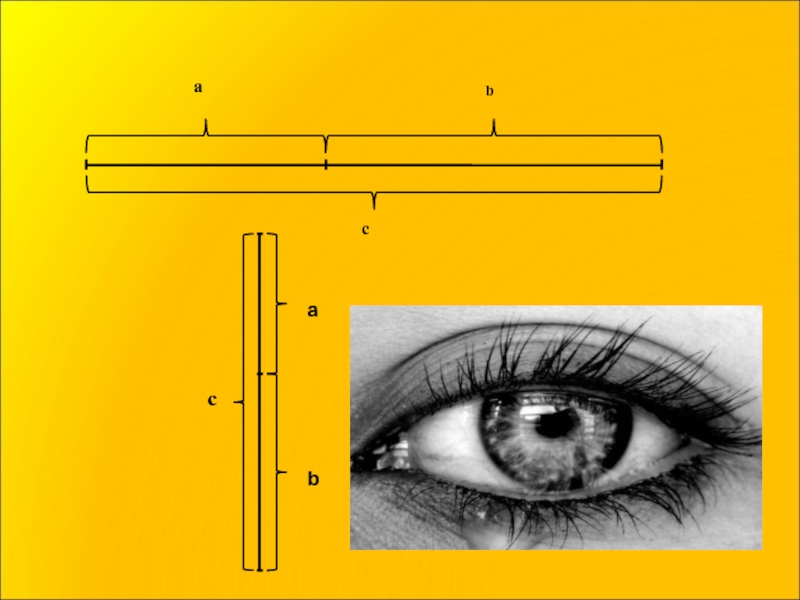
- 12. аb
- 13. Слайд 13
- 14. расстояние от талии
- 15. Слайд 15
- 16. Математика в архитектуре.
- 17. Практическое исследование. Кукольный театр в г. Дзержинске
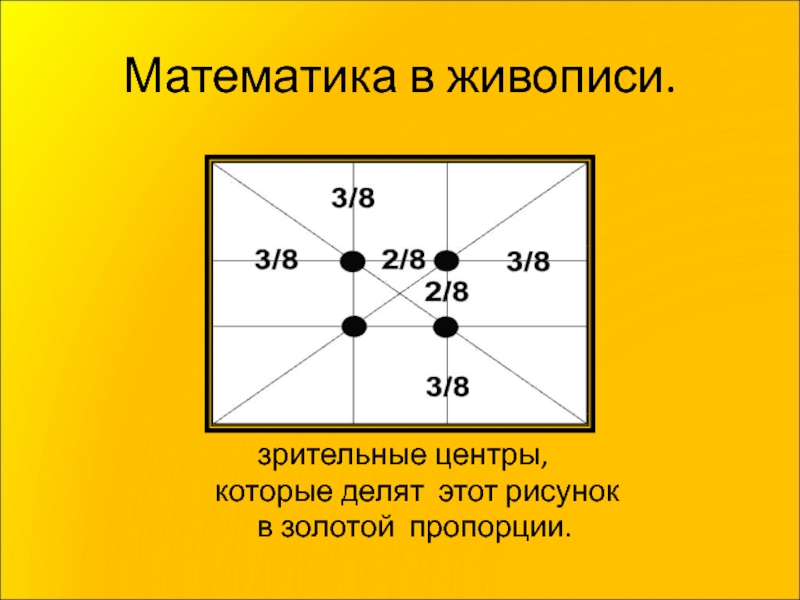
- 18. Математика в живописи.
- 19. Картина Леонардо да Винчи «Тайная вечеря» построена на золотых прямоугольниках.
- 20. Леонардо да Винчи «Мона Лиза» («Джоконда»)
- 21. Рафаэль «Избиение младенцев» На подготовительном
- 22. Практическое исследование. «Спас нерукотворный»
- 23. Математика и декоративно-прикладное искусство. Главную роль
- 24. Блюдо
- 25. Математика в литературе. Практическое исследование.
- 26. Л. Кэрролл «Алиса в Зазеркалье». Практическое исследование.
- 27. Слайд 27
- 28. Слайд 28
- 29. Слайд 29
- 30. В. Губарев «Королевство кривых зеркал» Практическое исследование. Оля и её симметричный двойник Яло.
- 31. Нушрок - КоршунАнидаг – Гадина Абаж -
- 32. Математика в музыке.
- 33. Практическое исследование. 30 см18 см48 см48 :
- 34. Все великие произведения искусства построены по
- 35. Бессмертие искусства - в математике!
Слайд 1Математика в искусстве.
выполнил:
Викулов Виталий,
ученик 9Б класса,
МБОУ СОШ №30
г.Дзержинска
руководители:
Бойко Г.И.
Викулова О.А.
Слайд 3
Гипотеза:
математика как наука имеет свои каноны красоты, которые используются
Цель работы -
показать связь математики и искусства.
Слайд 4
Задачи:
познакомиться с новыми математическими понятиями (золотой треугольник, золотое сечение,
произвести анализ разных видов искусства: живописи, архитектуры, скульптуры, литературы, музыки, прикладного искусства;
показать присутствие в них понятий арифметики, алгебры, геометрии;
произвести практическое исследование, как красота определённого произведения искусства (картины, архитектурного строения, литературного произведения) связана с математикой;
на основании всего изложенного сформулировать вывод о том, какую роль играет математика в искусстве.
Слайд 5 Геометрия владеет двумя сокровищами.
Иоганн Кеплер
Слайд 6Золотое сечение.
Золотым сечением (“божественной пропорцией”) называли математики
Это соотношение сводится к решению уравнения: b² = са
Это отношение приближенно равно 1,618…
оно получило название число Ф(фи)
в честь древнегреческого скульптора Фидия.
Если принять длину всего отрезка за единицу, то с = 1 b = х а = 1-х
При решении этого уравнения х² =1·(1-х) величина Х = 0, 618 …
следовательно, величина 1-Х = 0,382…
Значит, длина большего отрезка b будет равна 0,618…
длина меньшего отрезка a будет равна 1- 0,618 = 0,382…
Слайд 7Ряд Фибоначчи.
Месяцы 0 1 2 3 4
Пары кроликов 0 1 1 2 3 5 8 13 21 34 55 89 144 и т.д.
Этот ряд и получил название ряда Фибоначчи:
каждый его член, начиная с третьего, равен сумме двух предыдущих:
2 + 3 = 5; 3 + 5 = 8; 5 + 8 = 13, 8 + 13 = 21; 13 + 21 = 34
отношение смежных чисел ряда приближается к отношению золотого сечения:
например, 3 5 8 8:5 примерно равно 5:3
8:5 = 1,60 5:3 = 1,66…
если разделить каждый член этого ряда на предыдущий, полученные результаты будут стремиться к числу 1,618 , т.е. к числу Ф.
5:3=1.66… 13:8=1.625 21:13=1.615... 34:21=1.61…
Числа 0.618 и 0.382 являются коэффициентами последовательности Фибоначчи.
Слайд 8Спираль Фибоначчи.
У золотой спирали есть определенное начало и строится она
Слайд 9 Золотой прямоугольник.
Отношение смежных сторон дает пропорцию Фидия 1,618.
Если от него отрезать квадрат, то останется вновь золотой прямоугольник.
Слайд 10Золотой треугольник.
Отношение длины боковой стороны к длине основания
Длины биссектрис углов при его основании равны длине самого основания.
Слайд 11Звёздчатый пятиугольник.
Каждая из пяти линий, составляющая звездчатый пятиугольник, делит другую линию
Слайд 14
расстояние от талии до стопы кратно 0,618
от
т.е. составляет золотую пропорцию
a кратно 0,618
b кратно 0,382
Отношение a к b соответствует числу Ф,
т.е. равно 1,618
статуи Венеры Милосской и Аполлона Бельведерского
Математика в скульптуре.
0,618
0,382
Слайд 15
c=5,02
a=1,92
b=3,1
b : а = с : b
3,1 : 1,92 =1,614…
5,02 : 3,1 =1,619…
Оба эти значения близки к отношению золотого сечения 1,618
Практическое исследование.
a
b
c
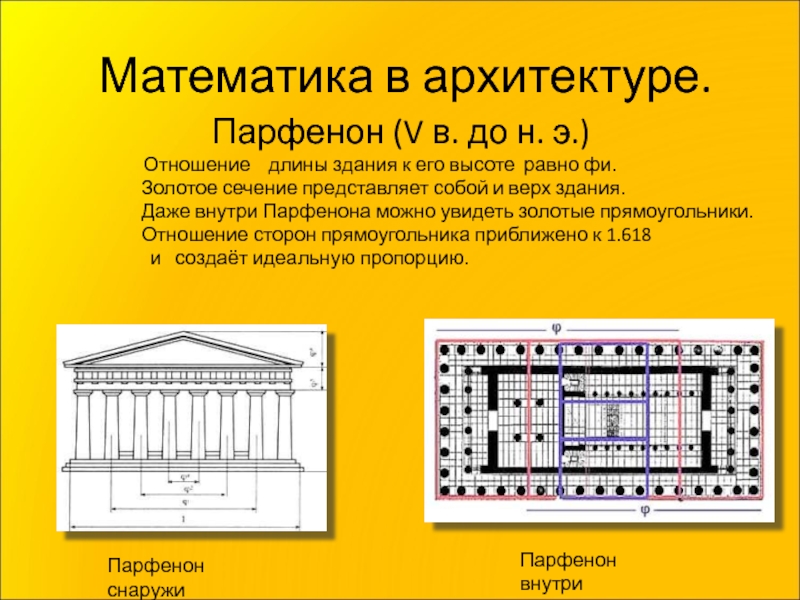
Слайд 16 Математика в архитектуре.
Отношение длины здания к его высоте равно фи.
Золотое сечение представляет собой и верх здания.
Даже внутри Парфенона можно увидеть золотые прямоугольники.
Отношение сторон прямоугольника приближено к 1.618
и создаёт идеальную пропорцию.
Парфенон снаружи
Парфенон внутри
Слайд 17Практическое исследование.
Кукольный театр в г. Дзержинске
с = 1,7
а = 0,65
b:а = 1,05:0,65 = 1,615…
с:b = 1,7:1, 05 = 1, 619…
эти значения близки к отношению золотой пропорции 1,618
a
φ²
φ
c
b
1
Слайд 20Леонардо да Винчи
«Мона Лиза» («Джоконда»)
Картина привлекательна тем, что
Мона Лиза – пример идеального изображения человека.
Слайд 21Рафаэль «Избиение младенцев»
На подготовительном эскизе Рафаэля проведены красные
Это можно проверить, измеряя отношение длин отрезков, высекаемых спиралью на прямых, проходящих через начало кривой.
Слайд 22Практическое исследование.
«Спас нерукотворный»
Божественный свет – это и
19,4 : 12 = 1,616…
12 : 7,4 = 1,62…
Даже на репродукции иконы эти значения близки к Ф.
7,4 см
12 см
19,4см
Слайд 23Математика и декоративно-прикладное искусство.
Главную роль здесь играет соблюдение закона
Наиболее распространенными мотивами этого вида прикладного искусства являются цветы
Слайд 25Математика в литературе. Практическое исследование.
Линейные перемещения: «Железная
Перемещение по плоскости: «Сентиментальное путешествие» Д. Стерна, «Письма русского путешественника» Н.М. Карамзина, «Дети капитана Гранта» Ж. Верна.
Перемещение в трёхмерном пространстве: «Из пушки на луну» Ж. Верна, «Вокруг света за 80 дней» Ж. Верна, «Гарри Поттер» Дж. Ролинг.
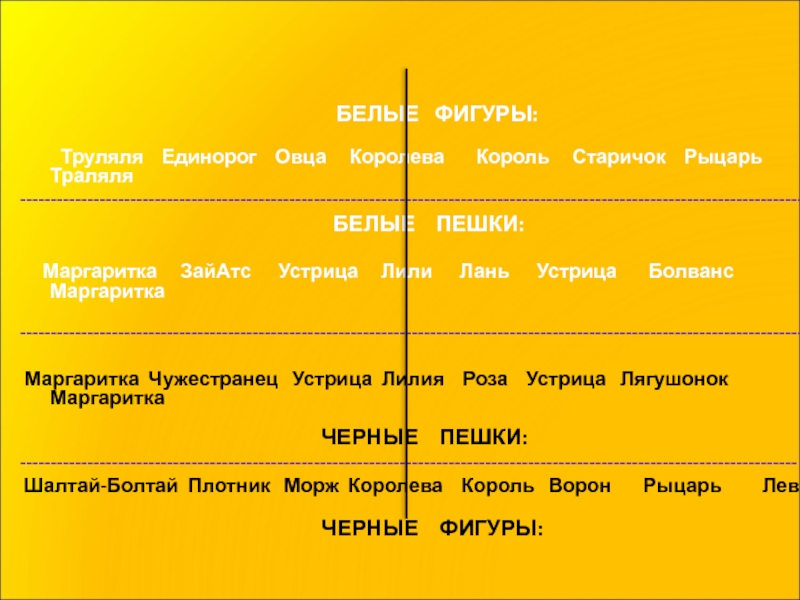
Слайд 29
БЕЛЫЕ ФИГУРЫ:
Труляля Единорог Овца Королева Король Старичок Рыцарь Траляля
--------------------------------------------------------------------------------------------------------------------------------
БЕЛЫЕ ПЕШКИ:
Маргаритка ЗайАтс Устрица Лили Лань Устрица Болванс Маргаритка
--------------------------------------------------------------------------------------------------------------------------------
Маргаритка Чужестранец Устрица Лилия Роза Устрица Лягушонок Маргаритка
ЧЕРНЫЕ ПЕШКИ:
-------------------------------------------------------------------------------------------------------------------------------
Шалтай-Болтай Плотник Морж Королева Король Ворон Рыцарь Лев
ЧЕРНЫЕ ФИГУРЫ:
Слайд 30 В. Губарев «Королевство кривых зеркал» Практическое исследование.
Оля и её
Слайд 31Нушрок - Коршун
Анидаг – Гадина
Абаж - Жаба
Топсед – Деспот
враги:
Яло
Гурд - Друг
Аксал – Ласка
Бар - Раб
друзья:
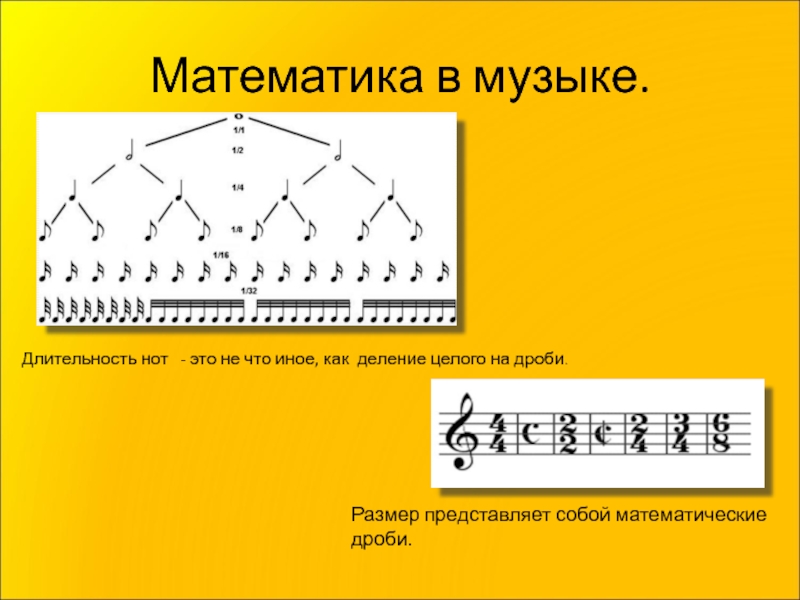
Слайд 32Математика в музыке.
Длительность нот
Размер представляет собой математические дроби.
Слайд 33Практическое исследование.
30 см
18 см
48 см
48 : 30 = 1,6
30 :
Это соотношение близко к числу Ф.