- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике Графический метод решения задач с параметрами
Содержание
- 1. Презентация по математике Графический метод решения задач с параметрами
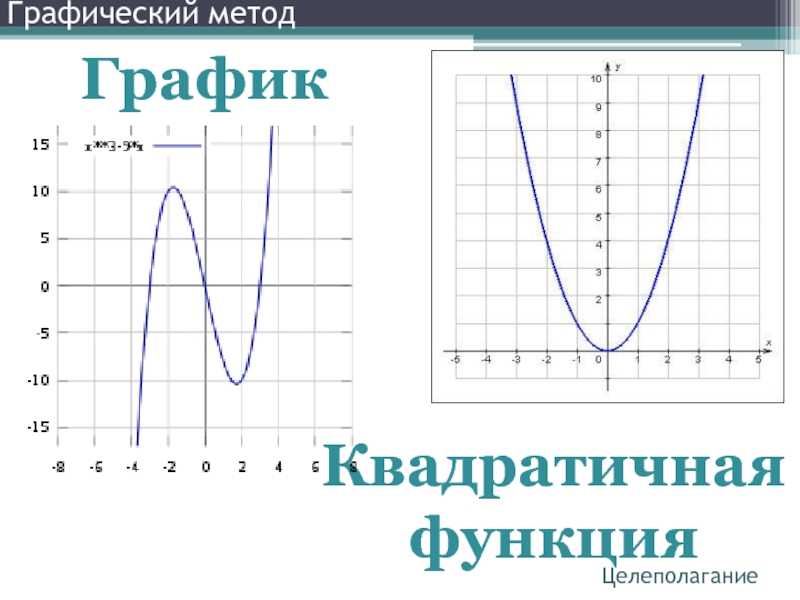
- 2. Графический методЦелеполаганиеГрафикКвадратичнаяфункция
- 3. 1)Что является графиком следующих функций? Вхождение в темуМатематическая разминкаОхарактеризуйте каждую из выше приведенных функцийГрафический метод
- 4. Организация учащихсяГрафический методТрудность решения в какой-то мере
- 5. Что значит графический метод?Любая задача с параметром
- 6. Что будет являться решением уравнения с одной
- 7. Решение. Рассмотрим функции
- 8. Решение. При |a|2 исходное неравенство будет выполняться при x>x2 и x
- 9. Рассмотрим ломанную f(x)=|x+2|-6 и семейство ломанных g(x,a)=-a|x-4|.ПрактикумПример2.
- 10. при a
- 11. при a=-1 части правых ветвей ломанной
- 12. при -1
- 13. при a=1 часть правой ветви f(x)
- 14. при a>1 графики семейства ломанных g(x,a)
- 15. Задание для самостоятельного решенияРешение. ОДЗ:Данное уравнение эквивалентно
- 16. Задание для самостоятельного решенияУравнение имеет единственный корень
- 17. Домашнее заданиеПри каких значениях параметра а уравнение
Слайд 1Графический метод
(квадратные уравнения и неравенства, уравнения с модулем)
Мельник П.И
ФМиКН,
5 курс
Слайд 31)Что является графиком следующих функций?
Вхождение в тему
Математическая разминка
Охарактеризуйте каждую из
Графический метод
Слайд 4Организация учащихся
Графический метод
Трудность решения в какой-то мере входит в само понятие
Д.Пойа
Слайд 5Что значит графический метод?
Любая задача с параметром есть задача как минимум
Координатно-графический метод представляет искомые решения в виде геометрического места точек на координатной плоскости, где в качестве одной из координат выступает параметр, а в качестве другой – искомая переменная.
Решение задачи в ином случае рассматривается как значение координаты, соответствующей искомой переменной, принадлежащей линии или области, задаваемой условием.
Графический метод
Освоение новых знаний
Слайд 6Что будет являться решением уравнения с одной переменной и одним параметром?
Графический
Первичное освоение темы
Что будет являться решением неравенства с одной переменной и одним параметром?
Что будет являться решением уравнения с двумя переменными и одним параметром?
Что будет являться решением неравенства с двумя переменными и одним параметром?
Подумаем?!
Слайд 7Решение. Рассмотрим функции
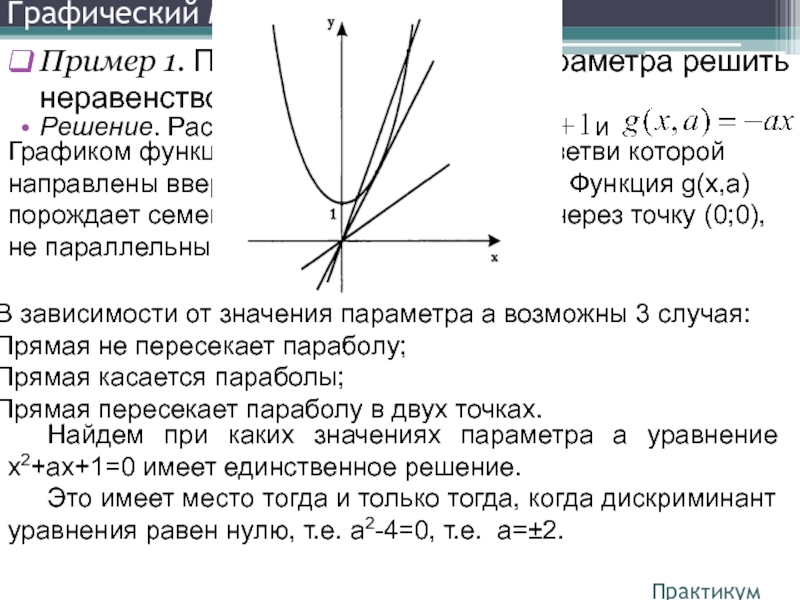
Пример 1. При каждом значении параметра решить неравенство
Практикум
Графиком функции f(x) является парабола, ветви которой направлены вверх, с вершиной в точке (0;1). Функция g(x,a) порождает семейство прямых, проходящих через точку (0;0), не параллельных оси OY.
Графический метод
Найдем при каких значениях параметра a уравнение x2+ax+1=0 имеет единственное решение.
Это имеет место тогда и только тогда, когда дискриминант уравнения равен нулю, т.е. a2-4=0, т.е. a=±2.
В зависимости от значения параметра a возможны 3 случая:
Прямая не пересекает параболу;
Прямая касается параболы;
Прямая пересекает параболу в двух точках.
Слайд 8Решение. При |a|
При |a|=2 парабола касается прямой и неравенство выполняется при всех , кроме тех, которые отвечают точкам касания, т.е. при x≠-1(если a=2) и x≠1 (если a=-2);
При |a|>2 исходное неравенство будет выполняться при x>x2
и x
Пример 1. При каждом значении параметра решить неравенство
Практикум
Ответ:
Графический метод
Слайд 9Рассмотрим ломанную f(x)=|x+2|-6 и семейство ломанных
g(x,a)=-a|x-4|.
Практикум
Пример2. При всех значениях параметра решить
Решение. Перепишем уравнение
Графический метод
Построим график ломанной f(x)=|x+2|-6
График ломанной f(x)=|x+2|-6 проходит через точку (4;0). Все ломанные семейства g(x,a)=-a|x-4| имеют «вершину» именно в этой точке.
Слайд 10при a
Практикум
Пример2. При всех значениях параметра решить уравнение.
Графический метод
Слайд 11 при a=-1 части правых ветвей ломанной и ломанных семейства g(x,a)
Практикум
Пример2. При всех значениях параметра решить уравнение.
Графический метод
Слайд 12 при -1
-x-2-6=a(x-4) x=(-8+4a)/(a+1).
Практикум
Пример2. При всех значениях параметра решить уравнение.
Графический метод
Слайд 13 при a=1 часть правой ветви f(x) совпадает с частью левой
Практикум
Пример2. При всех значениях параметра решить уравнение.
Графический метод
Слайд 14 при a>1 графики семейства ломанных g(x,a) будут симметричны относительно
Практикум
Пример2. При всех значениях параметра решить уравнение.
Графический метод
Ответ: а) при a<-1 и a>1 x=4;
б) при a=-1 x≥4;
в) при -1
Слайд 15Задание для самостоятельного решения
Решение. ОДЗ:
Данное уравнение эквивалентно системе:
Приведем ее к виду:
Проверка полученных результатов
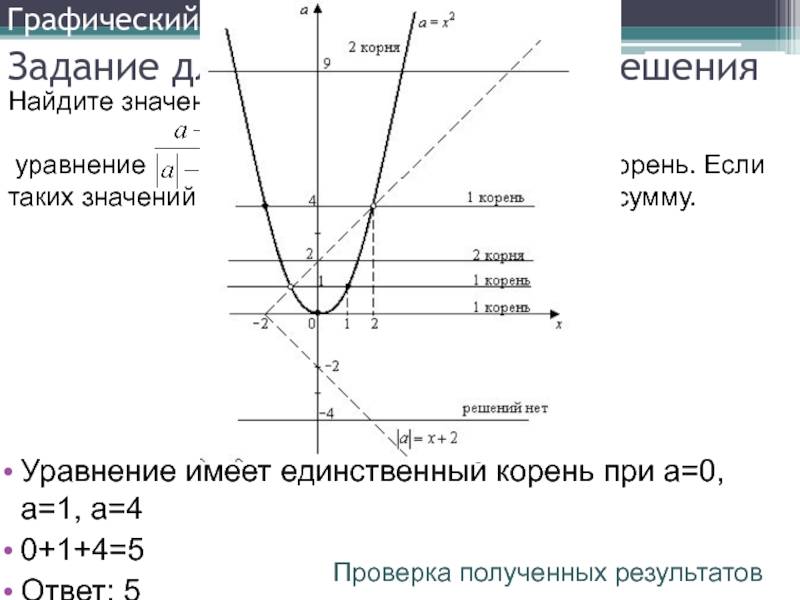
Найдите значение параметра а, при котором
уравнение имеет единственный корень. Если таких значений несколько, в ответе запишите их сумму.
Графический метод
Слайд 16Задание для самостоятельного решения
Уравнение имеет единственный корень при а=0, а=1, а=4
0+1+4=5
Ответ:
Проверка полученных результатов
Найдите значение параметра а, при котором
уравнение имеет единственный корень. Если таких значений несколько, в ответе запишите их сумму.
Графический метод
Слайд 17Домашнее задание
При каких значениях параметра а уравнение имеет ровно два решения?
Подведение
Величие человека - в его способности мыслить. Б. Паскаль
Графический метод
Какие были трудности на уроке?
Как вы их преодолели?
Остались ли непонятные моменты?