- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике Функции и их графики
Содержание
- 1. Презентация по математике Функции и их графики
- 2. ОглавлениеПонятие функцииПостоянная функцияКорень n-ой степениСтепенная функцияПоказательная функцияЛогарифмическая функцияТригонометрические функции
- 3. Понятие функцииПонятие функции является одним из основных
- 4. Постоянная функция
- 5. Постоянная функция задается на множестве всех действительных
- 6. Свойства постоянной функции: Область определения: все множество
- 7. Корень n-ой степени
- 8. Рассмотрим основную элементарную функцию, которая задается формулой
- 9. Свойства функции корень n-ой степени при четных n.Область определения:
- 10. Функция корень n-ой степени с нечетным показателем корня n определена
- 11. Свойства функции корень n-ой степени при нечетных n.Область определения:
- 12. Степенная функция
- 13. Степенная функция.Степенная функция задается формулой вида
- 14. Степенная функция с нечетным положительным показателем.Рассмотрим степенную
- 15. Свойства степенной функции с нечетным положительным показателем.Область
- 16. Степенная функция с четным положительным показателем.Рассмотрим степенную функцию с четным положительным показателем степени, то есть, при а=2,4,6,….
- 17. Свойства степенной функции с четным положительным показателем.Область
- 18. Степенная функция с нечетным отрицательным показателемПосмотрите на
- 19. Свойства степенной функции с нечетным отрицательным показателем.Область
- 20. Степенная функция с четным отрицательным показателем.Перейдем к степенной функции при а=-2,-4,-6,….
- 21. Свойства степенной функции с четным отрицательным показателем.Область
- 22. Степенная функция с рациональным или иррациональным показателем,
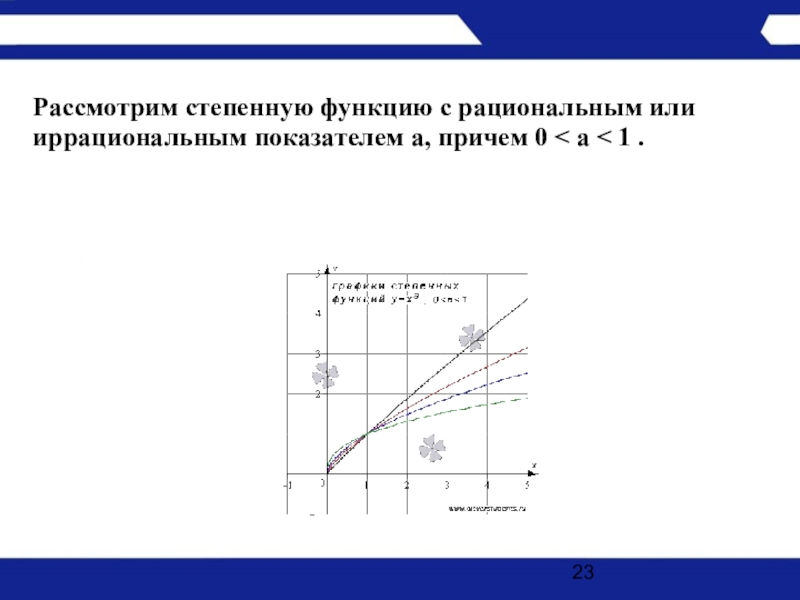
- 23. Рассмотрим степенную функцию с рациональным или иррациональным показателем a, причем 0 < a < 1 .
- 24. Свойства степенной функции при 0 < a <
- 25. Степенная функция с нецелым рациональным или иррациональным
- 26. Свойства степенной функции при a > 1.Область определения:
- 27. Степенная функция с действительным показателем, который больше
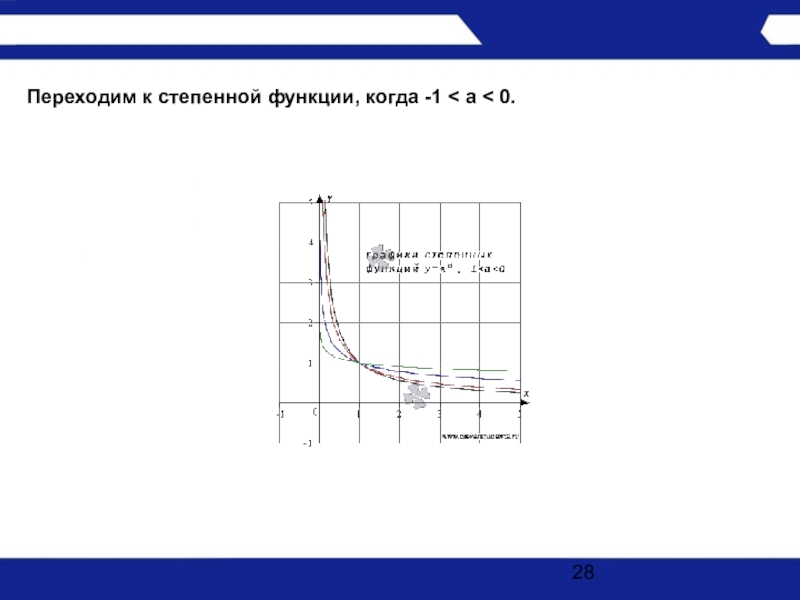
- 28. Переходим к степенной функции, когда -1 < a < 0.
- 29. Свойства степенной функции с показателем -1 < a
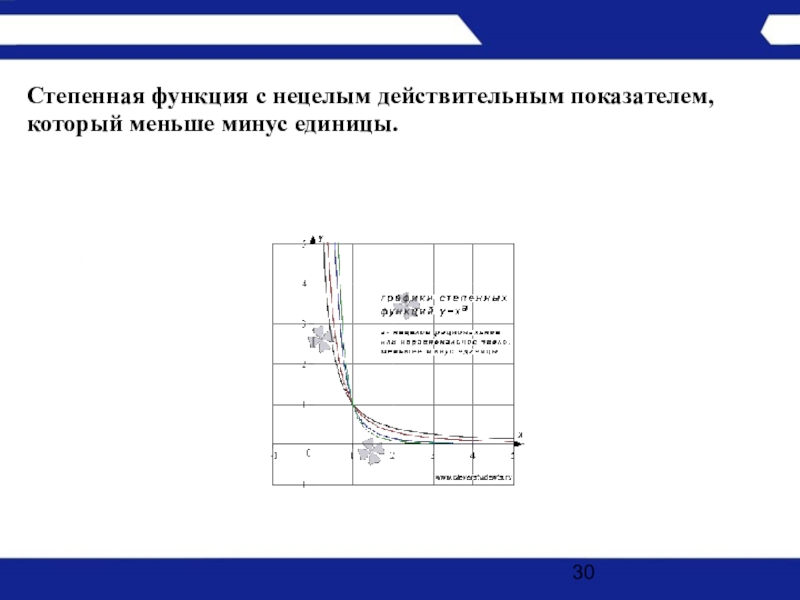
- 30. Степенная функция с нецелым действительным показателем, который меньше минус единицы.
- 31. Свойства степенной функции с нецелым отрицательным показателем,
- 32. Показательная функция
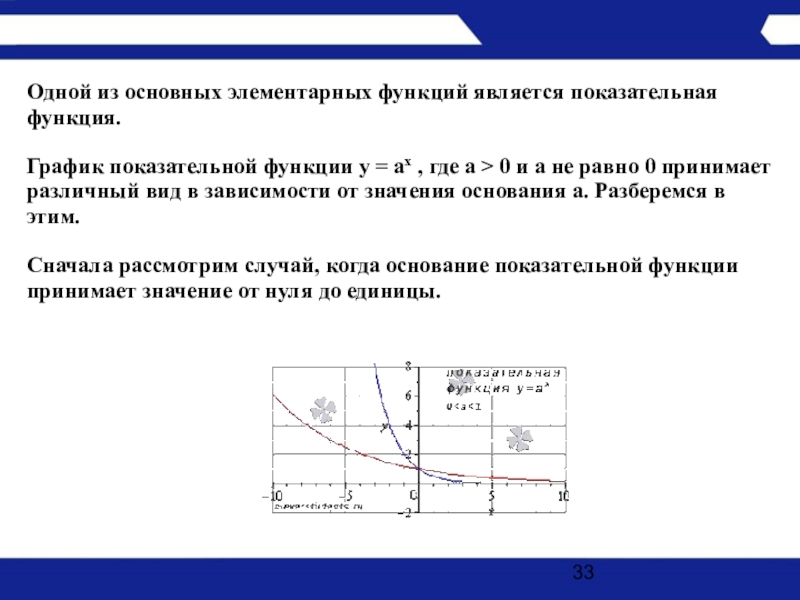
- 33. Одной из основных элементарных функций является показательная
- 34. Свойства показательной функции с основанием меньшим единицы.Областью
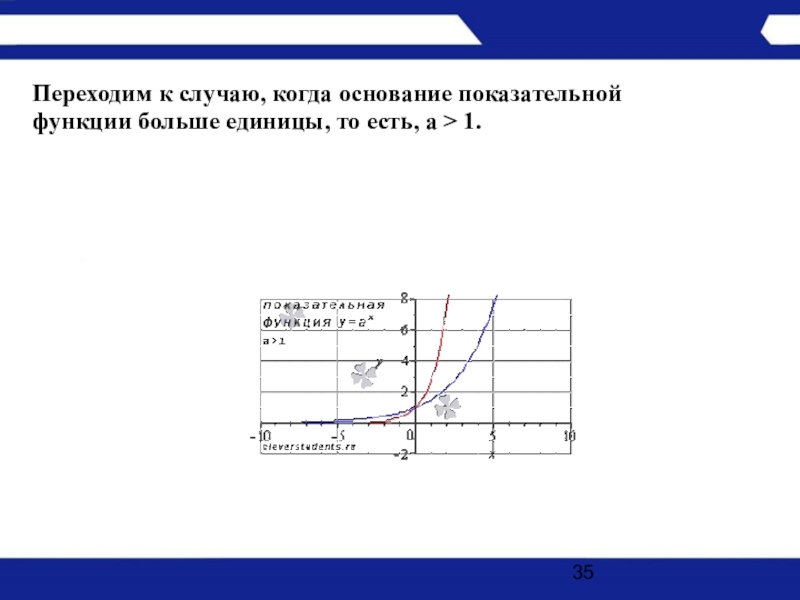
- 35. Переходим к случаю, когда основание показательной функции больше единицы, то есть, a > 1.
- 36. Свойства показательной функции с основанием большим единицы.Область
- 37. Логарифмическая функция
- 38. Следующей основной элементарной функцией является логарифмическая функция
- 39. Свойства логарифмической функции с основанием меньшим единицы.Область
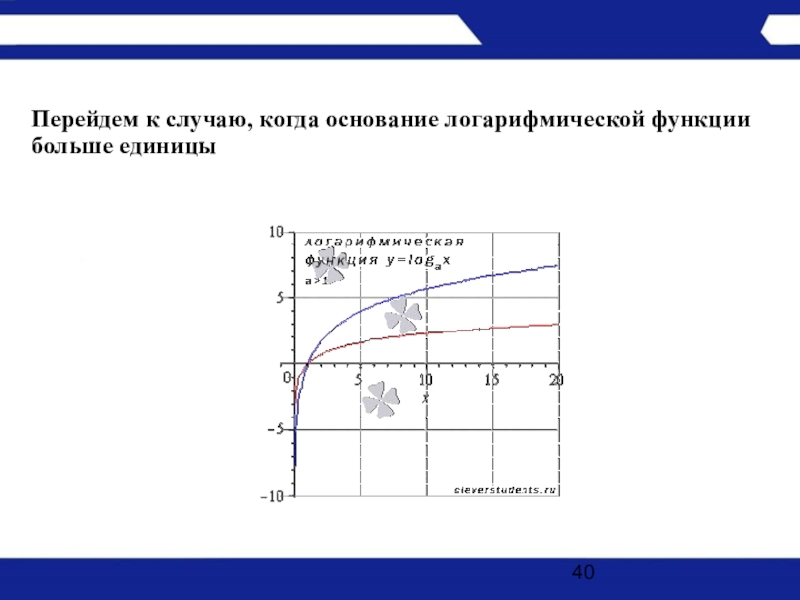
- 40. Перейдем к случаю, когда основание логарифмической функции больше единицы
- 41. Свойства логарифмической функции с основанием большим единицы.Область
- 42. Тригонометрические функции
- 43. Все тригонометрические функции (синус, косинус, тангенс и
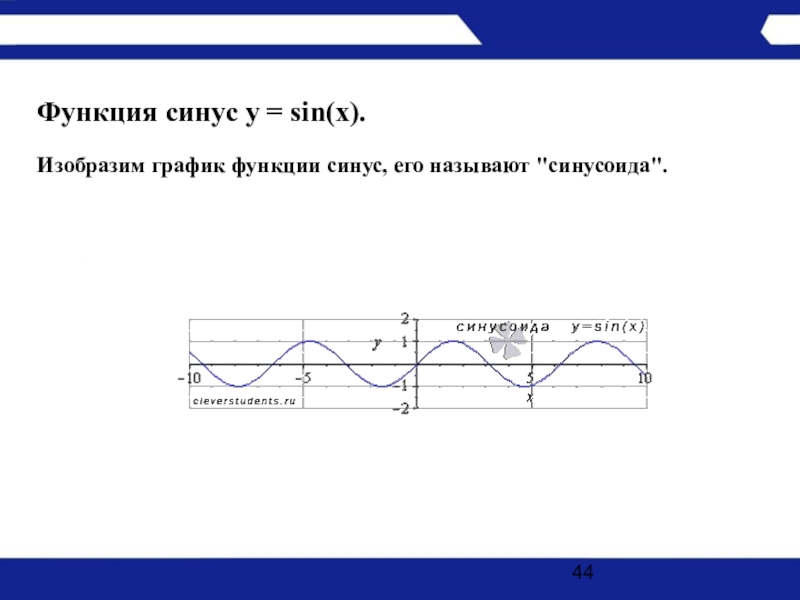
- 44. Функция синус y = sin(x).Изобразим график функции синус, его называют "синусоида".
- 45. Функция косинус y = cos(x).График функции косинус (его называют "косинусоида") имеет вид:
- 46. Функция тангенс y = tg(x).График функции тангенс (его называют "тангенсоида") имеет вид:
- 47. Функция котангенс y = ctg(x).Изобразим график функции котангенс (его называют "котангенсоида"):
ОглавлениеПонятие функцииПостоянная функцияКорень n-ой степениСтепенная функцияПоказательная функцияЛогарифмическая функцияТригонометрические функции
Слайд 2Оглавление
Понятие функции
Постоянная функция
Корень n-ой степени
Степенная функция
Показательная функция
Логарифмическая функция
Тригонометрические функции
Слайд 3Понятие функции
Понятие функции является одним из основных в математике. Оно вводится
следующим образом. Пусть заданы два множества X и Y. Если каждому элементу x из множества X поставлен в соответствие элемент y = f(x) множества Y, то говорят, что на множестве X задана функция f. При этом элемент x называется независимой переменной, а элемент y — зависимой переменной. В случае, когда x и y являются действительными числами, функцию y = f(x) можно представить в виде графика в декартовой системе координат Oxy.
Слайд 5Постоянная функция задается на множестве всех действительных чисел формулой y равно
C, где C – некоторое действительное число. Постоянная функция ставит в соответствие каждому действительному значению независимой переменной x одно и то же значение зависимой переменной y – значение С. Постоянную функцию также называют константой.
Графиком постоянной функции является прямая, параллельная оси абсцисс и проходящая через точку с координатами (0,C). Для примера покажем графики постоянных функций y=5, y=-2 и y равно кубическому корню из трех, которым на рисунке, приведенном ниже, отвечают черная, красная и синяя прямые соответственно.
Графиком постоянной функции является прямая, параллельная оси абсцисс и проходящая через точку с координатами (0,C). Для примера покажем графики постоянных функций y=5, y=-2 и y равно кубическому корню из трех, которым на рисунке, приведенном ниже, отвечают черная, красная и синяя прямые соответственно.
Слайд 6Свойства постоянной функции:
Область определения: все множество действительных чисел.
Постоянная функция является
четной.
Область значений: множество, состоящее из единственного числа С.
Постоянная функция невозрастающая и неубывающая (на то она и постоянная).
Говорить о выпуклости и вогнутости постоянной не имеет смысла.
Асимптот нет.
Функция проходит через точку (0,C) координатной плоскости.
Область значений: множество, состоящее из единственного числа С.
Постоянная функция невозрастающая и неубывающая (на то она и постоянная).
Говорить о выпуклости и вогнутости постоянной не имеет смысла.
Асимптот нет.
Функция проходит через точку (0,C) координатной плоскости.
Слайд 8Рассмотрим основную элементарную функцию, которая задается формулой
, где n – натуральное число, большее единицы.
Корень n-ой степени, n - четное число.
Начнем с функции корень n-ой степени при четных значениях показателя корня n.
Для примера приведем рисунок с изображениями графиков функций и, им соответствуют черная, красная и синяя линии.
Аналогичный вид имеют графики функций корень четной степени при других значениях показателя.
Корень n-ой степени, n - четное число.
Начнем с функции корень n-ой степени при четных значениях показателя корня n.
Для примера приведем рисунок с изображениями графиков функций и, им соответствуют черная, красная и синяя линии.
Аналогичный вид имеют графики функций корень четной степени при других значениях показателя.
Слайд 9Свойства функции корень n-ой степени при четных n.
Область определения: множество всех неотрицательных действительных
чисел .
При x=0 функция принимает значение, равное нулю.
Эта функция общего вида (не является четной или нечетной).
Область значений функции: все неотрицательные числа .
Функция, при четных показателях корня возрастает на всей области определения.
Эта функция имеет выпуклость, направленную вверх, на всей области определения, точек перегиба нет.
Асимптот нет.
График функции корень n-ой степени при четных n проходит через точки (0,0) и(1,1).
При x=0 функция принимает значение, равное нулю.
Эта функция общего вида (не является четной или нечетной).
Область значений функции: все неотрицательные числа .
Функция, при четных показателях корня возрастает на всей области определения.
Эта функция имеет выпуклость, направленную вверх, на всей области определения, точек перегиба нет.
Асимптот нет.
График функции корень n-ой степени при четных n проходит через точки (0,0) и(1,1).
Слайд 10Функция корень n-ой степени с нечетным показателем корня n определена на всем множестве действительных
чисел. Для примера приведем графики функций и, им соответствуют черная, красная и синяя кривые.
Слайд 11Свойства функции корень n-ой степени при нечетных n.
Область определения: множество всех действительных чисел.
Эта
функция нечетная.
Область значений функции: множество всех действительных чисел.
Функция при нечетных показателях корня возрастает на всей области определения.
Эта функция вогнутая на промежутке и выпуклая на промежутке , точка с координатами (0,0) – точка перегиба.
Асимптот нет.
График функции корень n-ой степени при нечетных n проходит через точки (-1,-1), (0,0) и (1,1).
Область значений функции: множество всех действительных чисел.
Функция при нечетных показателях корня возрастает на всей области определения.
Эта функция вогнутая на промежутке и выпуклая на промежутке , точка с координатами (0,0) – точка перегиба.
Асимптот нет.
График функции корень n-ой степени при нечетных n проходит через точки (-1,-1), (0,0) и (1,1).
Слайд 13Степенная функция.
Степенная функция задается формулой вида .
Рассмотрим
вид графиков степенной функции и свойства степенной функции в зависимости от значения показателя степени.
Начнем со степенной функции с целым показателем a. В этом случае вид графиков степенных функций и свойства функций зависят от четности или нечетности показателя степени, а также от его знака. Поэтому сначала рассмотрим степенные функции при нечетных положительных значениях показателя a, далее - при четных положительных, далее - при нечетных отрицательных показателях степени, и, наконец, при четных отрицательных a.
Свойства степенных функций с дробными и иррациональными показателями (как и вид графиков таких степенных функций) зависят от значения показателя a. Их будем рассматривать, во-первых, при a от нуля до единицы, во-вторых, при a больших единицы, в-третьих, при a от минус единицы до нуля, в-четвертых, при a меньших минус единицы.
В заключении этого пункта для полноты картины опишем степенную функцию с нулевым показателем.
Начнем со степенной функции с целым показателем a. В этом случае вид графиков степенных функций и свойства функций зависят от четности или нечетности показателя степени, а также от его знака. Поэтому сначала рассмотрим степенные функции при нечетных положительных значениях показателя a, далее - при четных положительных, далее - при нечетных отрицательных показателях степени, и, наконец, при четных отрицательных a.
Свойства степенных функций с дробными и иррациональными показателями (как и вид графиков таких степенных функций) зависят от значения показателя a. Их будем рассматривать, во-первых, при a от нуля до единицы, во-вторых, при a больших единицы, в-третьих, при a от минус единицы до нуля, в-четвертых, при a меньших минус единицы.
В заключении этого пункта для полноты картины опишем степенную функцию с нулевым показателем.
Слайд 14Степенная функция с нечетным положительным показателем.
Рассмотрим степенную функцию при нечетном положительном показателе
степени, то есть, при а=1,3,5,….
На рисунке ниже приведены графики степенных функций:
На рисунке ниже приведены графики степенных функций:
Слайд 15Свойства степенной функции с нечетным положительным показателем.
Область определения: все действительные числа .
Область
значений: все действительные числа.
Функция нечетная, так как y(-x) = -y(x).
Функция возрастает при любом значении.
Функция выпуклая при неположительных значениях и вогнутая при неотрицательных (кроме линейной функции).
Точка (0;0) является точкой перегиба (кроме линейной функции).
Асимптот нет.
Функция проходит через точки (-1;-1), (0;0), (1;1).
Функция нечетная, так как y(-x) = -y(x).
Функция возрастает при любом значении.
Функция выпуклая при неположительных значениях и вогнутая при неотрицательных (кроме линейной функции).
Точка (0;0) является точкой перегиба (кроме линейной функции).
Асимптот нет.
Функция проходит через точки (-1;-1), (0;0), (1;1).
Слайд 16Степенная функция с четным положительным показателем.
Рассмотрим степенную функцию с четным положительным показателем
степени, то есть, при а=2,4,6,….
Слайд 17Свойства степенной функции с четным положительным показателем.
Область определения: все действительные числа.
Область значений: все
действительные числа.
Функция четная, так как y(-x) = y(x).
Функция возрастает при неотрицательных значениях функции, убывает при неположительных.
Функция вогнутая при всех действительных значениях.
Точек перегиба нет.
Асимптот нет.
Функция проходит через точки (-1;1), (0;0), (1;1).
Функция четная, так как y(-x) = y(x).
Функция возрастает при неотрицательных значениях функции, убывает при неположительных.
Функция вогнутая при всех действительных значениях.
Точек перегиба нет.
Асимптот нет.
Функция проходит через точки (-1;1), (0;0), (1;1).
Слайд 18Степенная функция с нечетным отрицательным показателем
Посмотрите на графики степенной функции y
равно x в степени a при нечетных отрицательных значениях показателя степени, то есть, при а=-1,-3,-5,
Слайд 19Свойства степенной функции с нечетным отрицательным показателем.
Область определения: все действительные числа, кроме
нуля.
При x=0 имеем разрыв второго рода. Следовательно, прямая x=0 является вертикальной асимптотой.
Область значений: все действительные числа, кроме нуля.
Функция нечетная.
Функция убывает при любом значении.
Точек перегиба нет.
Горизонтальной асимптотой является прямая y = 0.
Функция проходит через точки (-1;-1), (1;1).
При x=0 имеем разрыв второго рода. Следовательно, прямая x=0 является вертикальной асимптотой.
Область значений: все действительные числа, кроме нуля.
Функция нечетная.
Функция убывает при любом значении.
Точек перегиба нет.
Горизонтальной асимптотой является прямая y = 0.
Функция проходит через точки (-1;-1), (1;1).
Слайд 20Степенная функция с четным отрицательным показателем.
Перейдем к степенной функции при а=-2,-4,-6,….
Слайд 21Свойства степенной функции с четным отрицательным показателем.
Область определения: все действительные числа, кроме
нуля.
При x=0 имеем разрыв второго рода. Следовательно, прямая x=0 является вертикальной асимптотой.
Область значений: все положительные числа.
Функция четная
Функция возрастает при отрицательных значениях, убывает при положительных .
Точек перегиба нет.
Горизонтальной асимптотой является прямая y=0.
Функция проходит через точки (-1;1), (1;1).
При x=0 имеем разрыв второго рода. Следовательно, прямая x=0 является вертикальной асимптотой.
Область значений: все положительные числа.
Функция четная
Функция возрастает при отрицательных значениях, убывает при положительных .
Точек перегиба нет.
Горизонтальной асимптотой является прямая y=0.
Функция проходит через точки (-1;1), (1;1).
Слайд 22Степенная функция с рациональным или иррациональным показателем, значение которого больше нуля
и меньше единицы.
Обратите внимание! Если a - положительная дробь с нечетным знаменателем, то некоторые авторы считают областью определения степенной функции интервал . При этом оговариваются, что показатель степени a – несократимая дробь. Сейчас авторы многих учебников по алгебре и началам анализа НЕ ОПРЕДЕЛЯЮТ степенные функции с показателем в виде дроби с нечетным знаменателем при отрицательных значениях аргумента. Мы будем придерживаться именно такого взгляда, то есть, будем считать областями определения степенных функций с дробными положительными показателями степени множество.
Обратите внимание! Если a - положительная дробь с нечетным знаменателем, то некоторые авторы считают областью определения степенной функции интервал . При этом оговариваются, что показатель степени a – несократимая дробь. Сейчас авторы многих учебников по алгебре и началам анализа НЕ ОПРЕДЕЛЯЮТ степенные функции с показателем в виде дроби с нечетным знаменателем при отрицательных значениях аргумента. Мы будем придерживаться именно такого взгляда, то есть, будем считать областями определения степенных функций с дробными положительными показателями степени множество.
Слайд 23Рассмотрим степенную функцию с рациональным или иррациональным показателем a, причем 0 < a
< 1 .
Слайд 24Свойства степенной функции при 0 < a < 1.
Область определения: все неотрицательные
числа .
Область значений: все неотрицательные числа.
Функция не является ни четной, ни нечетной, то есть она общего вида.
Функция возрастает при неотрицательных значениях.
Функция выпуклая при положительных значениях.
Точек перегиба нет.
Асимптот нет.
Функция проходит через точки (0;0), (1;1).
Область значений: все неотрицательные числа.
Функция не является ни четной, ни нечетной, то есть она общего вида.
Функция возрастает при неотрицательных значениях.
Функция выпуклая при положительных значениях.
Точек перегиба нет.
Асимптот нет.
Функция проходит через точки (0;0), (1;1).
Слайд 25Степенная функция с нецелым рациональным или иррациональным показателем, большим единицы.
Рассмотрим степенную
функцию с нецелым рациональным или иррациональным показателем a, причем a > 1 .
Слайд 26Свойства степенной функции при a > 1.
Область определения: все неотрицательные числа.
Область значений:
все неотрицательные числа .
Функция не является ни четной, ни нечетной, то есть она общего вида.
Функция возрастает при неотрицательных значениях .
Функция вогнутая при положительных значениях , если 1 < a < 2 ; при неотрицательных значениях , если a > 2 .
Точек перегиба нет.
Асимптот нет.
Функция проходит через точки (0;0), (1;1).
Функция не является ни четной, ни нечетной, то есть она общего вида.
Функция возрастает при неотрицательных значениях .
Функция вогнутая при положительных значениях , если 1 < a < 2 ; при неотрицательных значениях , если a > 2 .
Точек перегиба нет.
Асимптот нет.
Функция проходит через точки (0;0), (1;1).
Слайд 27Степенная функция с действительным показателем, который больше минус единицы и меньше
нуля.
Обратите внимание! Если a - отрицательная дробь с нечетным знаменателем, то некоторые авторы считают областью определения степенной функции интервал . При этом оговариваются, что показатель степени a – несократимая дробь. Сейчас авторы многих учебников по алгебре и началам анализа НЕ ОПРЕДЕЛЯЮТ степенные функции с показателем в виде дроби с нечетным знаменателем при отрицательных значениях аргумента. Мы будем придерживаться именно такого взгляда, то есть, будем считать областями определения степенных функций с дробными дробными отрицательными показателями степени множество соответственно.
Обратите внимание! Если a - отрицательная дробь с нечетным знаменателем, то некоторые авторы считают областью определения степенной функции интервал . При этом оговариваются, что показатель степени a – несократимая дробь. Сейчас авторы многих учебников по алгебре и началам анализа НЕ ОПРЕДЕЛЯЮТ степенные функции с показателем в виде дроби с нечетным знаменателем при отрицательных значениях аргумента. Мы будем придерживаться именно такого взгляда, то есть, будем считать областями определения степенных функций с дробными дробными отрицательными показателями степени множество соответственно.
Слайд 29Свойства степенной функции с показателем -1 < a < 0
Область определения: все положительные
числа.
х=0 является вертикальной асимптотой.
Область значений: все положительные числа.
Функция не является ни четной, ни нечетной, то есть она общего вида.
Функция убывает при положительных значениях.
Функция вогнутая при положительных значениях.
Точек перегиба нет.
Горизонтальной асимптотой является прямая y=0.
Функция проходит через точку (1;1).
х=0 является вертикальной асимптотой.
Область значений: все положительные числа.
Функция не является ни четной, ни нечетной, то есть она общего вида.
Функция убывает при положительных значениях.
Функция вогнутая при положительных значениях.
Точек перегиба нет.
Горизонтальной асимптотой является прямая y=0.
Функция проходит через точку (1;1).
Слайд 31Свойства степенной функции с нецелым отрицательным показателем, меньшим минус единицы.
Область определения: все
положительные числа.
х=0 является вертикальной асимптотой.
Область значений: все отрицательные числа.
Функция не является ни четной, ни нечетной, то есть она общего вида.
Функция убывает при положительных значениях.
Функция вогнутая при положительных значениях.
Точек перегиба нет.
Горизонтальной асимптотой является прямая y=0.
Функция проходит через точку (1;1).
х=0 является вертикальной асимптотой.
Область значений: все отрицательные числа.
Функция не является ни четной, ни нечетной, то есть она общего вида.
Функция убывает при положительных значениях.
Функция вогнутая при положительных значениях.
Точек перегиба нет.
Горизонтальной асимптотой является прямая y=0.
Функция проходит через точку (1;1).
Слайд 33Одной из основных элементарных функций является показательная функция.
График показательной функции y =
ax , где a > 0 и a не равно 0 принимает различный вид в зависимости от значения основания а. Разберемся в этим.
Сначала рассмотрим случай, когда основание показательной функции принимает значение от нуля до единицы.
Сначала рассмотрим случай, когда основание показательной функции принимает значение от нуля до единицы.
Слайд 34Свойства показательной функции с основанием меньшим единицы.
Областью определения показательной функции является
все множество действительных чисел: .
Область значений: все положительные числа .
Функция не является ни четной, ни нечетной, то есть, она общего вида.
Показательная функция, основание которой меньше единицы, убывает на всей области определения.
Функция вогнутая при любых значениях.
Точек перегиба нет.
Горизонтальной асимптотой является прямая y = 0 при х стремящемся к плюс бесконечности.
Функция проходит через точку (0;1).
Область значений: все положительные числа .
Функция не является ни четной, ни нечетной, то есть, она общего вида.
Показательная функция, основание которой меньше единицы, убывает на всей области определения.
Функция вогнутая при любых значениях.
Точек перегиба нет.
Горизонтальной асимптотой является прямая y = 0 при х стремящемся к плюс бесконечности.
Функция проходит через точку (0;1).
Слайд 36Свойства показательной функции с основанием большим единицы.
Область определения показательной функции: любое действительное
число.
Область значений: все положительные числа.
Функция не является ни четной, ни нечетной, то есть она общего вида.
Показательная функция, основание которой больше единицы, возрастает при .
Функция вогнутая при любом значении.
Точек перегиба нет.
Горизонтальной асимптотой является прямая y = 0 при х стремящемся к минус бесконечности.
Функция проходит через точку (0;1).
Область значений: все положительные числа.
Функция не является ни четной, ни нечетной, то есть она общего вида.
Показательная функция, основание которой больше единицы, возрастает при .
Функция вогнутая при любом значении.
Точек перегиба нет.
Горизонтальной асимптотой является прямая y = 0 при х стремящемся к минус бесконечности.
Функция проходит через точку (0;1).
Слайд 38Следующей основной элементарной функцией является логарифмическая функция y = log a
(x) , где a > 0, a не равно 1 , . Логарифмическая функция определена лишь для положительных значений аргумента.
График логарифмической функции принимает различный вид в зависимости от значения основания а.
Начнем со случая, когда 0 < a < 1.
График логарифмической функции принимает различный вид в зависимости от значения основания а.
Начнем со случая, когда 0 < a < 1.
Слайд 39Свойства логарифмической функции с основанием меньшим единицы.
Область определения логарифмической функции: все
положительные числа . При х стремящемся к нулю справа, значения функции стремятся к плюс бесконечности.
Область значений: любое число .
Функция не является ни четной, ни нечетной, то есть она общего вида.
Логарифмическая функция убывает на всей области определения.
Функция вогнутая при положительных значениях.
Точек перегиба нет.
Горизонтальных асимптот нет.
Функция проходит через точку (1;0).
Область значений: любое число .
Функция не является ни четной, ни нечетной, то есть она общего вида.
Логарифмическая функция убывает на всей области определения.
Функция вогнутая при положительных значениях.
Точек перегиба нет.
Горизонтальных асимптот нет.
Функция проходит через точку (1;0).
Слайд 41Свойства логарифмической функции с основанием большим единицы.
Область определения: все положительные числа .
При х стремящемся к нулю справа, значения функции стремятся к минус бесконечности.
Областю значений логарифмической функции является все множество действительных чисел.
Функция не является ни четной, ни нечетной, то есть она общего вида.
Функция возрастает при положительных значениях .
Функция выпуклая при положительных значениях.
Точек перегиба нет.
Горизонтальных асимптот нет.
Функция проходит через точку (1;0).
Областю значений логарифмической функции является все множество действительных чисел.
Функция не является ни четной, ни нечетной, то есть она общего вида.
Функция возрастает при положительных значениях .
Функция выпуклая при положительных значениях.
Точек перегиба нет.
Горизонтальных асимптот нет.
Функция проходит через точку (1;0).
Слайд 43Все тригонометрические функции (синус, косинус, тангенс и котангенс) относятся к основным
элементарным функциям. Сейчас мы рассмотрим их графики и перечислим свойства.
Тригонометрическим функциям присуще понятие периодичности (повторяемости значений функции при различных значениях аргумента, отличных друг от друга на величину периода f(x + T) = f(x) , где Т - период), поэтому, в список свойств тригонометрических функций добавлен пункт «наименьший положительный период». Также для каждой тригонометрической функции мы укажем значения аргумента, при которых соответствующая функция обращается в ноль.
Теперь разберемся со всеми тригонометрическими функциями по-порядку.
Тригонометрическим функциям присуще понятие периодичности (повторяемости значений функции при различных значениях аргумента, отличных друг от друга на величину периода f(x + T) = f(x) , где Т - период), поэтому, в список свойств тригонометрических функций добавлен пункт «наименьший положительный период». Также для каждой тригонометрической функции мы укажем значения аргумента, при которых соответствующая функция обращается в ноль.
Теперь разберемся со всеми тригонометрическими функциями по-порядку.