- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике для 11 класса Интегралы. Применение интегралов
Содержание
- 1. Презентация по математике для 11 класса Интегралы. Применение интегралов
- 2. Материал темы разбивается на параграфы:Первообразная, основное свойство
- 3. ЧАСТЬ 1 (ВВОДНАЯ)Учащиеся выбирают карточки, которые включают
- 4. Карточка 1. Определение первообразной.Вычислите интегралы:
- 5. Карточка 2.Что называется решением дифференциального уравнения?Решите неравенство
- 6. Карточка 3. Определение криволинейной трапеции.Решите уравнение
- 7. Карточка 4.Определенный интеграл.Найдите производную функции Вычислите площадь фигуры, ограниченной линиями
- 8. Карточка 5.Формула Ньютона – Лейбница.Решите уравнение Вычислите площадь фигуры, ограниченной линиями
- 9. Карточка 6.Правило вычисления определенного интеграла.Вычислите интегралы:
- 10. ЧАСТЬ 2 (ОСНОВНАЯ)Задачи разбиваются на три группы
- 11. ГРУППА 1
- 12. Вычислите площадь криволинейной трапеции, ограниченной заданными линиями :
- 13. Вычислите интегралы :
- 14. ГРУППА 2.
- 15. 1. Вычислите площадь фигуры, ограниченной графиком функции
- 16. 5. Вычислите площадь фигуры, ограниченной графиком функции
- 17. 10. Фигура ограничена линиями Найдите отношение
- 18. Вычислите интегралы
- 19. Найдите объем тела, полученного при вращении вокруг
- 20. Вычислите интегралы
- 21. ГРУППА 3.
- 22. Найдите площадь фигуры, ограниченной осью абсцисс и
- 23. 4. Пользуясь геометрическим смыслом определенного интеграла, вычислите5.
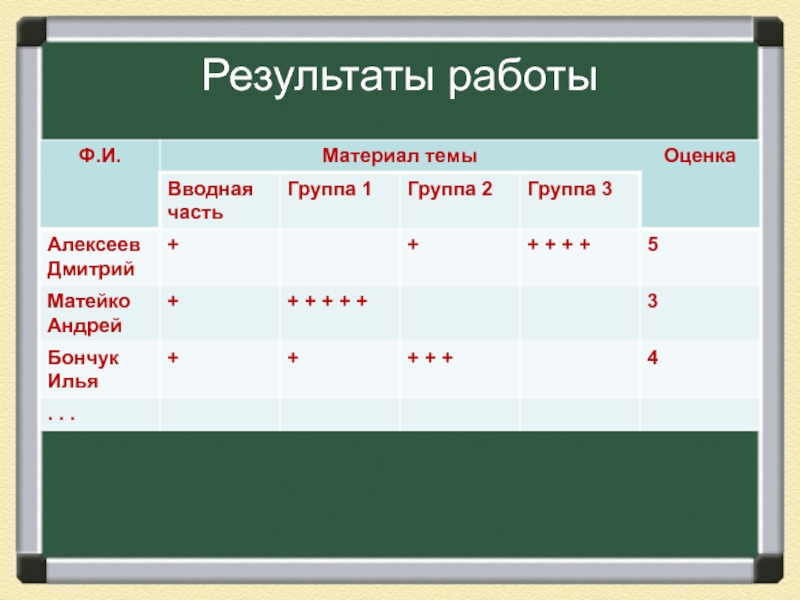
- 24. Результаты работы
- 25. ЧАСТЬ 3Задания этой части известны учащимся за
- 26. 1.Найдите площадь фигуры, ограниченной линиями у2 =
- 27. 5. Найдите площадь фигуры, ограниченной графиком функции
- 28. Найдите площадь фигуры, ограниченной линиями у =
- 29. 10. При каких а площадь криволинейной трапеции,
- 30. Литература Саакян С., Гольдман А., Денисов Д.
- 31. Слайд 31
Слайд 1Интегралы.
Применение интегралов.
Релейный зачет
11 класс
Ерёмина Людмила Александровна –
учитель математики МАУ ШИЛИ
г.Калининград
Слайд 2Материал темы разбивается на параграфы:
Первообразная, основное свойство первообразной.
Определенный интеграл. Площадь криволинейной
Формула Ньютона – Лейбница.
Вычисление площадей плоских фигур с помощью интегралов. Вычисление объемов.
Дифференциальные уравнения, их решение. Дифференциальные уравнения с разделяющимися переменными.
Нестандартные задачи.
Слайд 3ЧАСТЬ 1 (ВВОДНАЯ)
Учащиеся выбирают карточки, которые включают теорию и задачи. Карточки
Слайд 4Карточка 1.
Определение первообразной.
Вычислите интегралы:
Вычислите площадь фигуры, ограниченной линиями ,
.
,
.
Слайд 5Карточка 2.
Что называется решением дифференциального уравнения?
Решите неравенство
Вычислите площадь фигуры, ограниченной
и
Слайд 6Карточка 3.
Определение криволинейной трапеции.
Решите уравнение
Докажите, что функция является первообразной для функции
Слайд 7Карточка 4.
Определенный интеграл.
Найдите производную функции
Вычислите площадь фигуры, ограниченной линиями
Слайд 8Карточка 5.
Формула Ньютона – Лейбница.
Решите уравнение
Вычислите площадь фигуры, ограниченной
Слайд 9Карточка 6.
Правило вычисления определенного интеграла.
Вычислите интегралы:
Найдите А и В,
удовлетворяет условиям
и
Слайд 10ЧАСТЬ 2 (ОСНОВНАЯ)
Задачи разбиваются на три группы по степени сложности. В
Слайд 15
1. Вычислите площадь фигуры, ограниченной графиком функции
2. Найдите площадь фигуры, ограниченной линиями
3. Найдите площадь фигуры, ограниченной линиями
4. Вычислите площадь фигуры, ограниченной графиком функции касательной к графику в его точке с абсциссой х0= и прямой
Слайд 16
5. Вычислите площадь фигуры, ограниченной графиком функции определенной на
6. Найдите площадь фигуры, ограниченной линиями
7. Найдите площадь фигуры, ограниченной линиями
8. Найдите площадь фигуры, ограниченной линиями
9. Найдите площадь фигуры, ограниченной линиями
Слайд 17
10. Фигура ограничена линиями
Найдите отношение площадей фигур, на которые
11. Найдите площадь фигуры, ограниченной линиями
12. Найдите площадь фигуры, ограниченной линиями
Слайд 19Найдите объем тела, полученного при вращении вокруг оси абсцисс фигуры, ограниченной
И
4.
Слайд 22
Найдите площадь фигуры, ограниченной осью абсцисс и графиком функции
Изобразите на координатной плоскости линию, задаваемую уравнением
и найдите площадь фигуры, ограниченной этой линией.
3. Пользуясь геометрическим смыслом определенного интеграла, вычислите
Слайд 23
4. Пользуясь геометрическим смыслом определенного интеграла, вычислите
5. Решите неравенство
6. Найдите
7. Найдите минимумы функции
Слайд 25ЧАСТЬ 3
Задания этой части известны учащимся за две недели до зачета.
Слайд 26
1.Найдите площадь фигуры, ограниченной линиями у2 = х и х +
2.Найдите площадь фигуры, ограниченной линиями у = х2+2 | х | -8 и у =4- х2.
3. Найдите площадь фигуры, ограниченной линиями у=|х2-3х | + х и у = х+4.
4. Вычислить площадь фигуры, ограниченной графиком функции у = , касательной к графику этой функции в точке с абсциссой х0=1 и прямой х=3 (
Слайд 27
5. Найдите площадь фигуры, ограниченной графиком функции
у =
6. Фигура, ограниченная линиями у = -2х+8, х=-1, у=0, делится параболой у = х2-4х+5 на две части. Найдите площадь каждой части.
Слайд 28
Найдите площадь фигуры, ограниченной линиями у = у
8. Найдите площадь фигуры, ограниченной кривой у = и прямой, проходящей через точки А (2;2) и В (4;3).
9. Найдите площадь фигуры, ограниченной кривой у = х2 - 2х, касательной к этой кривой в точке с абсциссой х0=3 и прямой х=-1.
Слайд 29
10. При каких а площадь криволинейной трапеции, ограниченной линиями у =
11. Докажите, что при всех k площадь фигуры, ограниченной графиком функции f (х)= k2х5 – kх2 и осью абсцисс, не зависит от k.
12. Вычислите определенный интеграл, пользуясь его геометрической интерпретацией:
Слайд 30Литература
Саакян С., Гольдман А., Денисов Д. «Задачи по алгебре и началам
Сборник конкурсных задач по математике/ Под ред. М.Сканави. М.: Высшая школа, 2003
Галицкий М.Л., Мошкович М.М., Шварцбурд С.И. «Углубленное изучение курса алгебры и математического анализа (пособие для учителя). М.: Просвещение, 1995
Звавич Л.И., Рязановский А.Р., Поташник А.М. «Сборник задач по алгебре и математическому анализу. Выпуск 1. Интеграл и площадь». М.: Новая школа, 1996