- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике 10 класс Введение в стереометрию. Аксиомы стериометрии
Содержание
- 1. Презентация по математике 10 класс Введение в стереометрию. Аксиомы стериометрии
- 2. Я думаю, что никогда до настоящего времени
- 3. Постройте четыре равносторонних треугольника
- 4. ГеометрияПланиметрияСтереометрияЭто раздел математики, изучающий пространственные отношения и
- 5. Предмет стереометрии. Первый дошедший до нас
- 6. Пирамида Хеопса
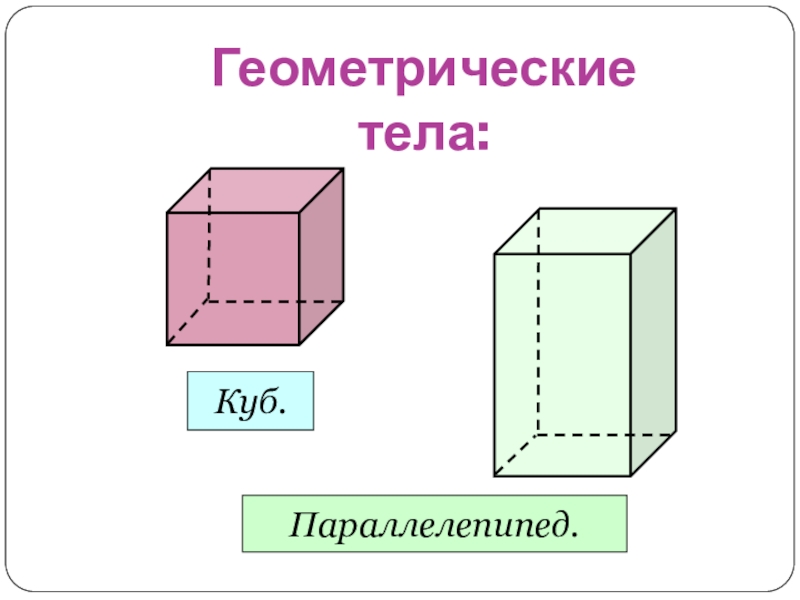
- 7. Геометрические тела:Куб.Параллелепипед.
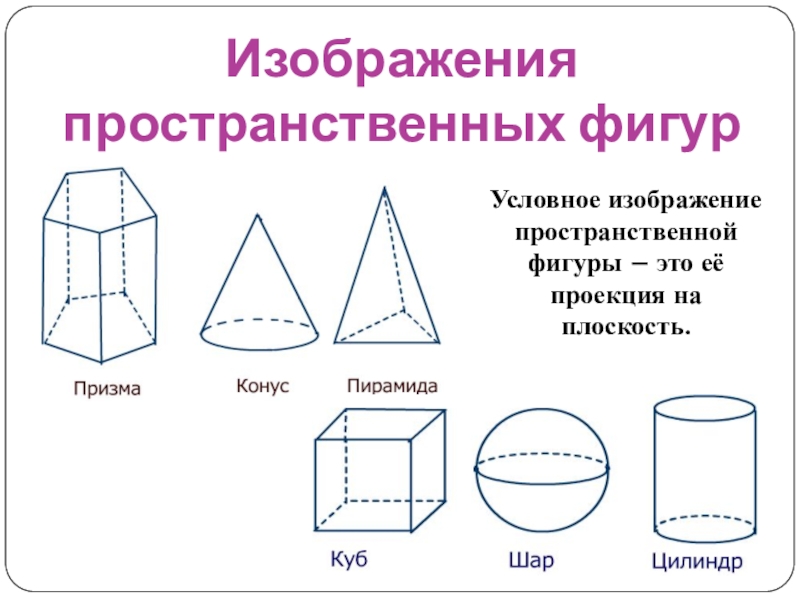
- 8. Изображения пространственных фигур Условное изображение пространственной фигуры – это её проекция на плоскость.
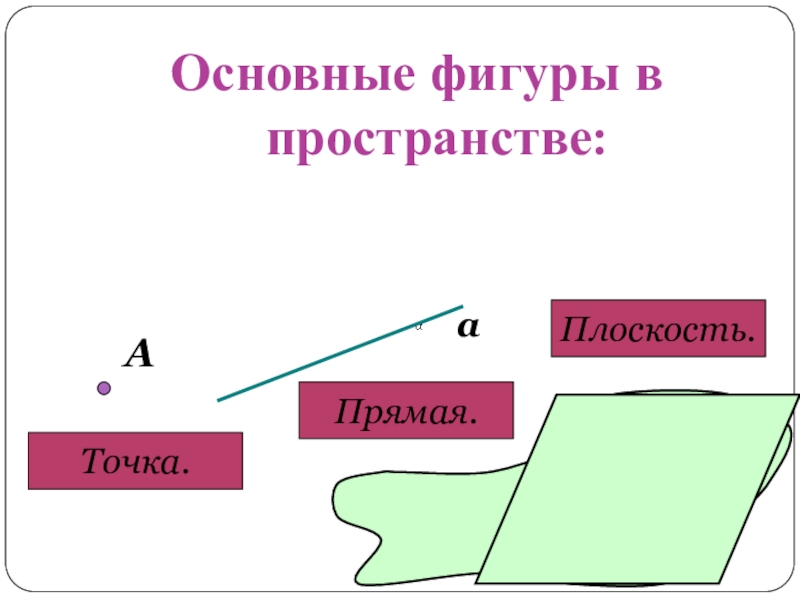
- 9. Основные фигуры в пространстве:АТочка.аПрямая.Плоскость.
- 10. A, B, C, …a, b, c, …илиAВ, BС, CD, …
- 11. Аксиома(от греч. axíõma – принятие положения)исходное положение научной теории, принимаемое без доказательства
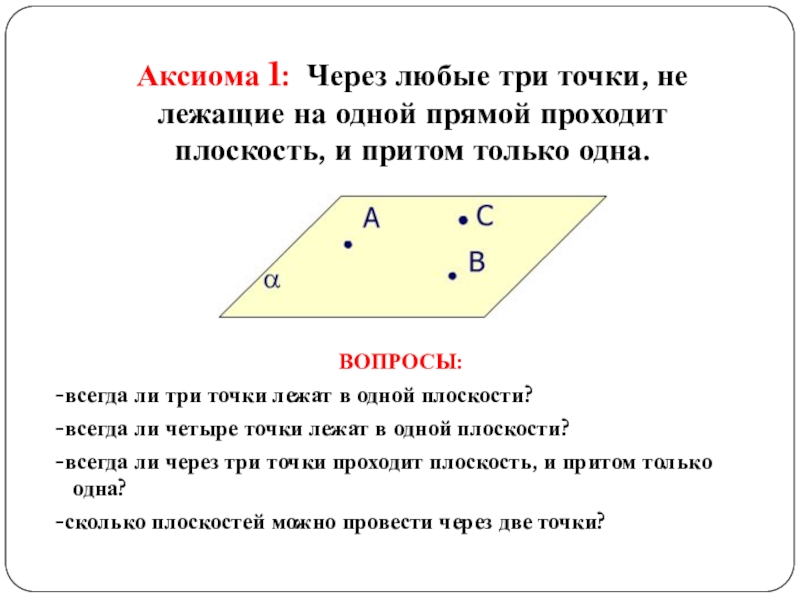
- 12. Аксиома 1: Через любые три точки, не
- 13. Аксиома 2: Если две точки прямой лежат
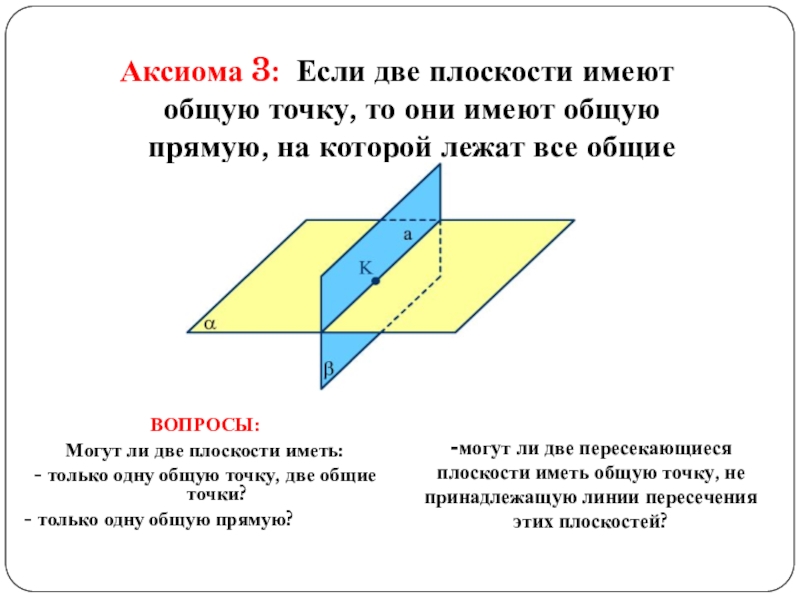
- 14. Аксиома 3: Если две плоскости имеют общую
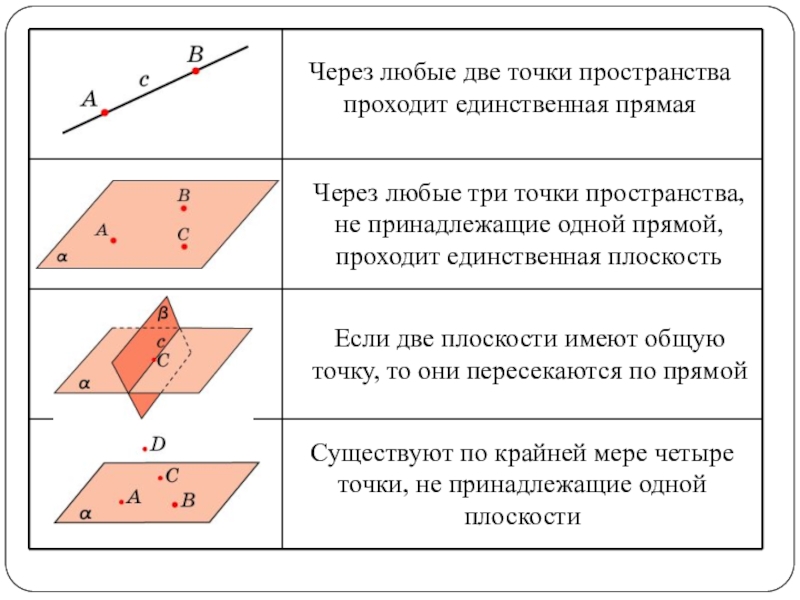
- 15. АКСИОМЫ СТЕРЕОМЕТРИИЧерез любые две точки пространства проходит
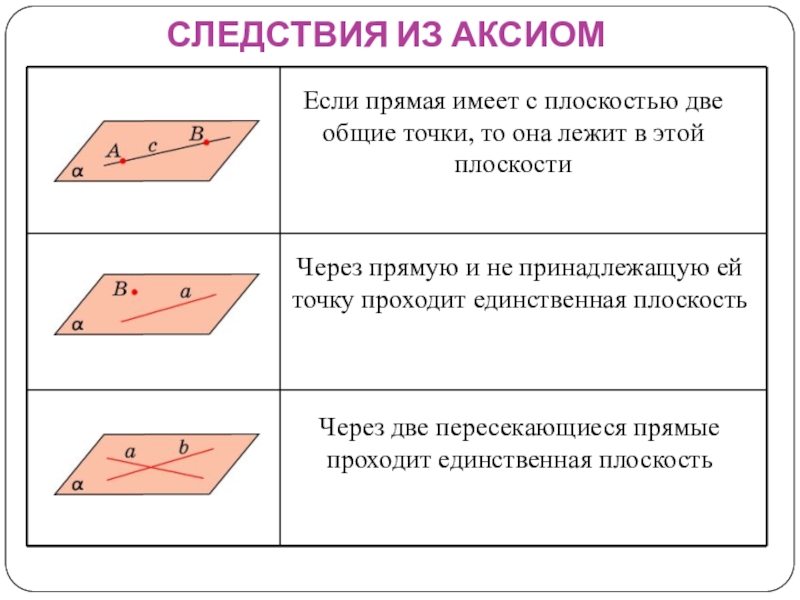
- 16. СЛЕДСТВИЯ ИЗ АКСИОМЕсли прямая имеет с плоскостью
Слайд 2Я думаю, что никогда до настоящего времени мы не жили в
Ле Корбюзье
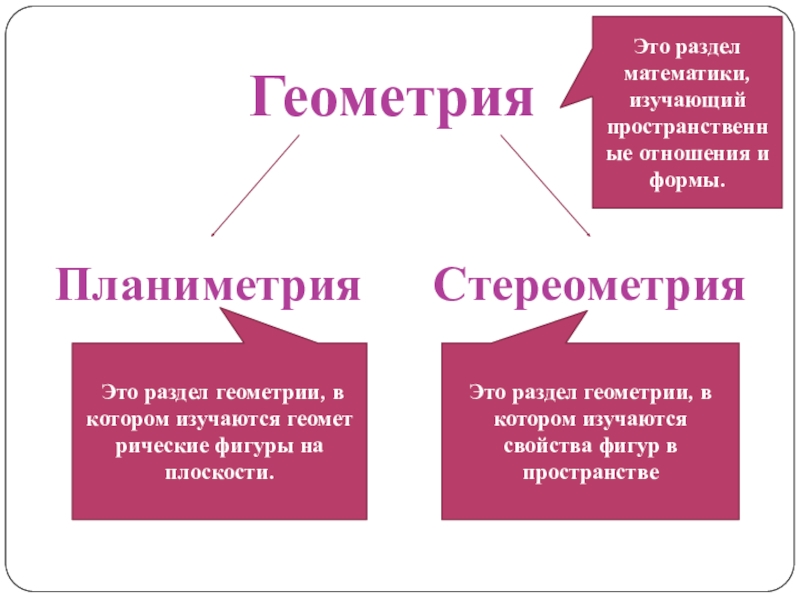
Слайд 4Геометрия
Планиметрия
Стереометрия
Это раздел математики, изучающий пространственные отношения и формы.
Это раздел геометрии, в котором изучаются геометрические фигуры на
Это раздел геометрии, в котором изучаются свойства фигур в пространстве
Слайд 5Предмет стереометрии.
Первый дошедший до нас учебник – руководство по
Слайд 8Изображения пространственных фигур
Условное изображение пространственной фигуры – это
Слайд 11Аксиома
(от греч. axíõma – принятие положения)
исходное положение научной теории, принимаемое без
Слайд 12Аксиома 1: Через любые три точки, не лежащие на одной прямой
ВОПРОСЫ:
-всегда ли три точки лежат в одной плоскости?
-всегда ли четыре точки лежат в одной плоскости?
-всегда ли через три точки проходит плоскость, и притом только одна?
-сколько плоскостей можно провести через две точки?
Слайд 13Аксиома 2: Если две точки прямой лежат в плоскости, то все
ВОПРОСЫ:
верно ли утверждение:
- если две точки окружности лежат в плоскости, то и вся окружность лежит в этой плоскости?
- а если три точки окружности лежат в плоскости, то …?
Слайд 14Аксиома 3: Если две плоскости имеют общую точку, то они имеют
ВОПРОСЫ:
Могут ли две плоскости иметь:
- только одну общую точку, две общие точки?
- только одну общую прямую?
-могут ли две пересекающиеся плоскости иметь общую точку, не принадлежащую линии пересечения этих плоскостей?
Слайд 15АКСИОМЫ СТЕРЕОМЕТРИИ
Через любые две точки пространства проходит единственная прямая
Через любые три
Если две плоскости имеют общую точку, то они пересекаются по прямой
Существуют по крайней мере четыре точки, не принадлежащие одной плоскости
Слайд 16СЛЕДСТВИЯ ИЗ АКСИОМ
Если прямая имеет с плоскостью две общие точки, то
Через прямую и не принадлежащую ей точку проходит единственная плоскость
Через две пересекающиеся прямые проходит единственная плоскость