- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии Расстояние от точки до плоскости(10 класс)
Содержание
- 1. Презентация по геометрии Расстояние от точки до плоскости(10 класс)
- 2. Теоретический опрос.Угол между прямыми равен 900. Как
- 3. Теоретический опрос.Как определяется расстояние от точки до
- 4. Изучение нового.Рассмотрим плоскость α и точку А
- 5. Замечание 1.Если две плоскости параллельны, то все
- 6. Замечание 2.Если прямая параллельна плоскости, то все
- 7. Замечание 3.Если две прямые скрещивающиеся, то через
- 8. Решить задачи.№ 138 (а)№ 139 (а)№ 140№ 143
- 9. № 138(а)Подсказки: Воспользуйтесь соотношением сторон и
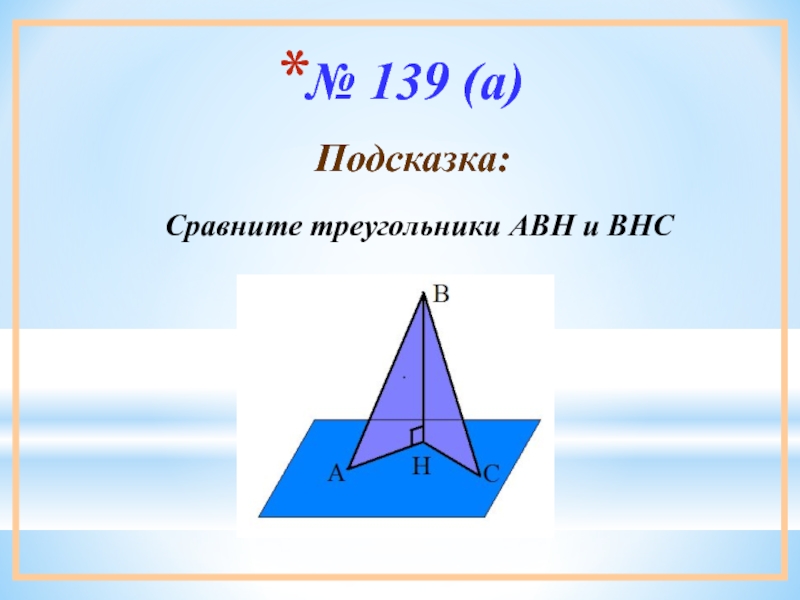
- 10. № 139 (а)Сравните треугольники АВН и ВНСПодсказка:
- 11. № 140Подсказки:Сравните треугольники АВО и АСОНайдите АВ
- 12. № 143Подсказки: Опустите перпендикуляр МО к плоскости
- 13. Если точка равноудалена от всех вершин многоугольника,
- 14. Докажите, что любая точка прямой, перпендикулярной плоскости
- 15. Назовите все наклонные к плоскости αНазовите проекции
- 16. α || β, назовите цвет линии, определяющей
- 17. Назовите цвет линии, определяющей расстояние между скрещивающимися прямыми
- 18. Домашнее заданиеТеория: пункт 19, стр. 40-41Задачи: №
Слайд 2Теоретический опрос.
Угол между прямыми равен 900. Как называются такие прямые?
Верно ли
Продолжите предложение: «Прямая перпендикулярна плоскости, если она …»
Что можно сказать о двух (3-х, 4-х) прямых, перпендикулярных к одной плоскости?
Две прямые, перпендикулярны третьей прямой, …
Слайд 3Теоретический опрос.
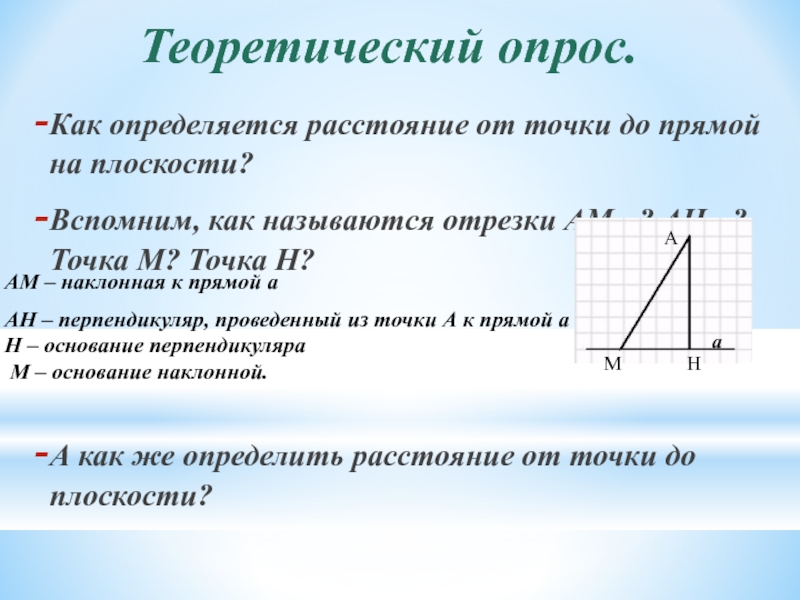
Как определяется расстояние от точки до прямой на плоскости?
Вспомним, как
А как же определить расстояние от точки до плоскости?
A
M
H
АМ – наклонная к прямой а
АН – перпендикуляр, проведенный из точки А к прямой а
Н – основание перпендикуляра
М – основание наклонной.
a
Слайд 4Изучение нового.
Рассмотрим плоскость α и точку А α
А
1) Через точку
2) Отметим в плоскости α произвольную точку М, отличную от Н.
М
АМ – наклонная, проведённая из А к плоскости α, НМ – её проекция на плоскость α.
3) Докажите, что АН<АМ; чему равен ∟МНА?
∟МНА= 900, значит ∆АНМ – прямоугольный: АН – катет, АМ - гипотенуза, следовательно АН<АМ
Вывод. Перпендикуляр, проведенный из данной точки к плоскости, меньше любой наклонной, проведенной из той же точки к этой плоскости. Длину перпендикуляра будем называть расстоянием от точки А до плоскости α.
Слайд 5Замечание 1.
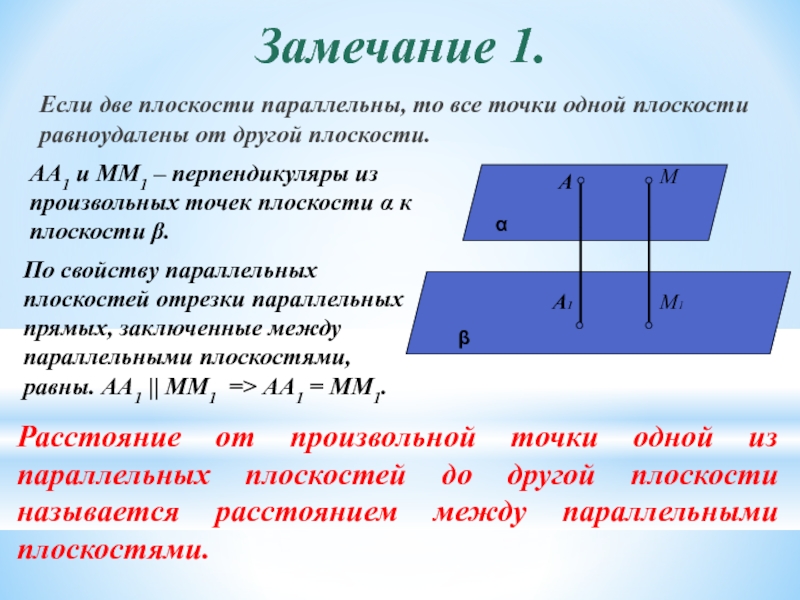
Если две плоскости параллельны, то все точки одной плоскости равноудалены
АА1 и ММ1 – перпендикуляры из произвольных точек плоскости α к плоскости β.
По свойству параллельных плоскостей отрезки параллельных прямых, заключенные между параллельными плоскостями, равны. АА1 || ММ1 => АА1 = ММ1.
Расстояние от произвольной точки одной из параллельных плоскостей до другой плоскости называется расстоянием между параллельными плоскостями.
Слайд 6Замечание 2.
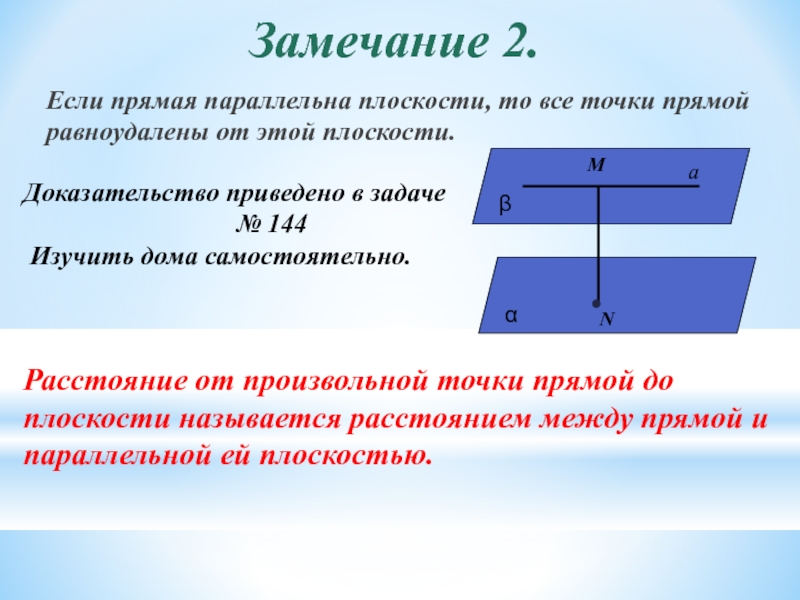
Если прямая параллельна плоскости, то все точки прямой равноудалены от
Доказательство приведено в задаче
№ 144
Изучить дома самостоятельно.
Расстояние от произвольной точки прямой до плоскости называется расстоянием между прямой и параллельной ей плоскостью.
Слайд 7Замечание 3.
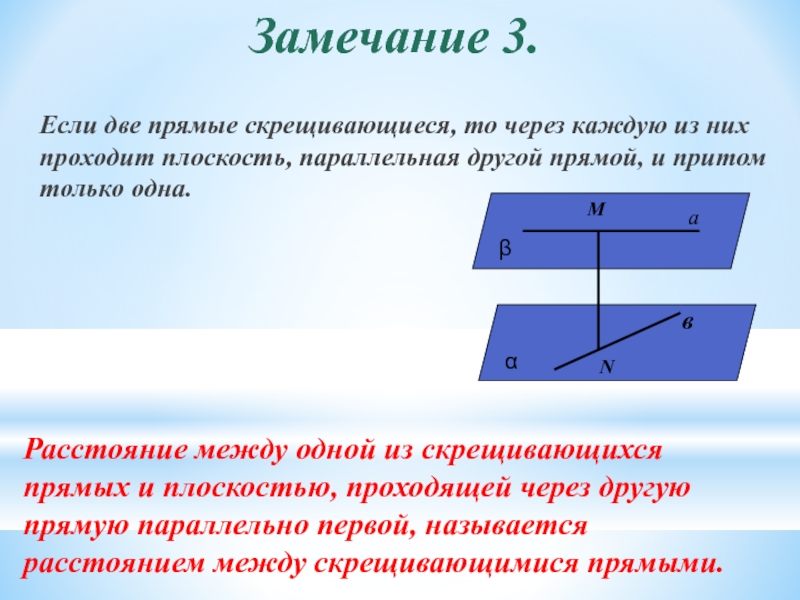
Если две прямые скрещивающиеся, то через каждую из них проходит
Расстояние между одной из скрещивающихся прямых и плоскостью, проходящей через другую прямую параллельно первой, называется расстоянием между скрещивающимися прямыми.
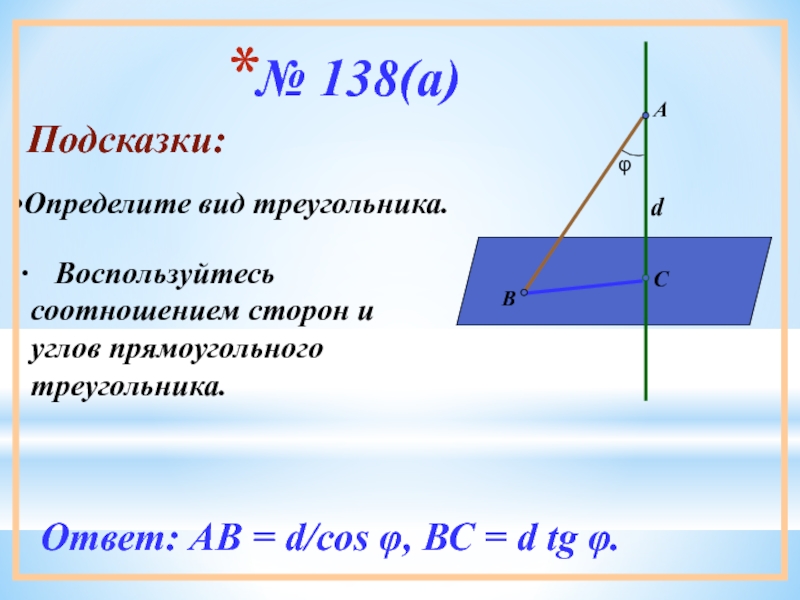
Слайд 9№ 138(а)
Подсказки:
Воспользуйтесь соотношением сторон и углов прямоугольного треугольника.
Ответ: АВ
Определите вид треугольника.
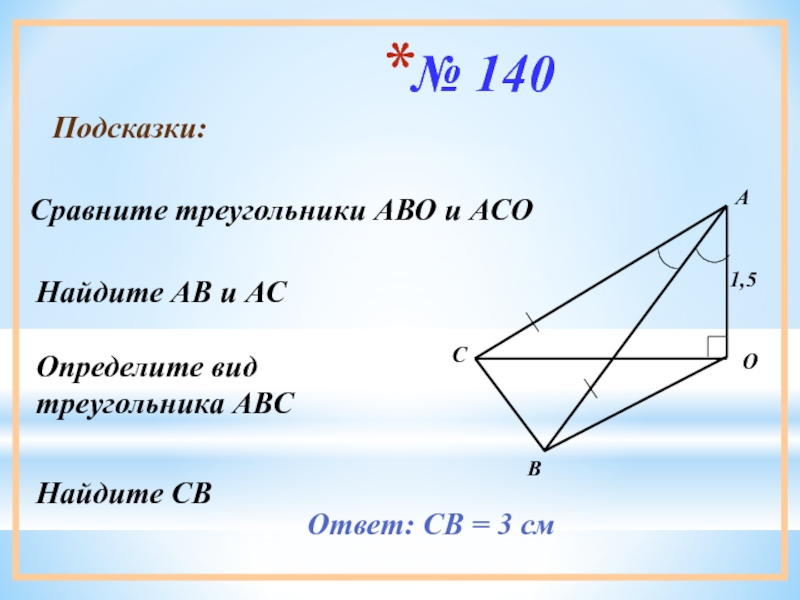
Слайд 11№ 140
Подсказки:
Сравните треугольники АВО и АСО
Найдите АВ и АС
Определите вид треугольника
Найдите СВ
Ответ: СВ = 3 см
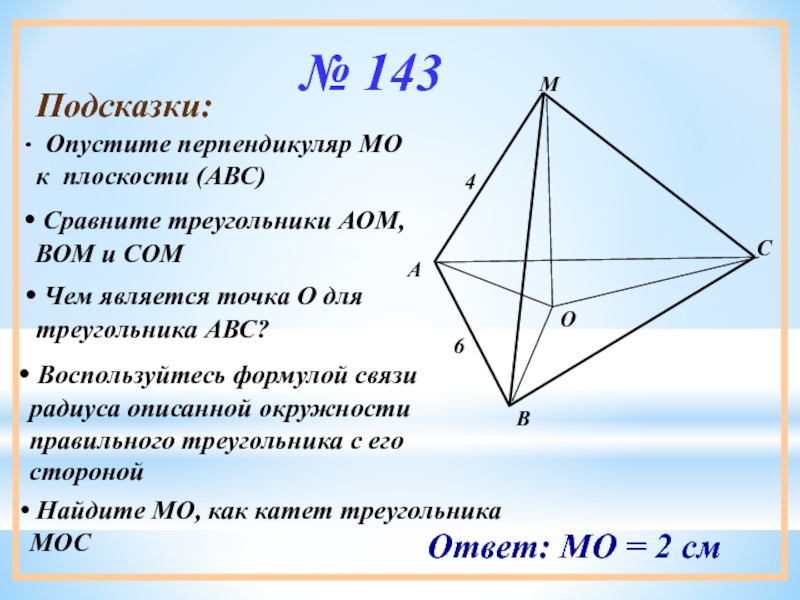
Слайд 12№ 143
Подсказки:
Опустите перпендикуляр МО к плоскости (АВС)
Сравните треугольники АОМ,
Чем является точка О для треугольника АВС?
Воспользуйтесь формулой связи радиуса описанной окружности правильного треугольника с его стороной
Найдите МО, как катет треугольника МОС
Ответ: МО = 2 см
Слайд 13Если точка равноудалена от всех вершин многоугольника, то во что она
Какой вывод можно сделать из решения этой задачи?
Если точка равноудалена от всех вершин многоугольника, то она проецируется в центр описанной окружности на его плоскости
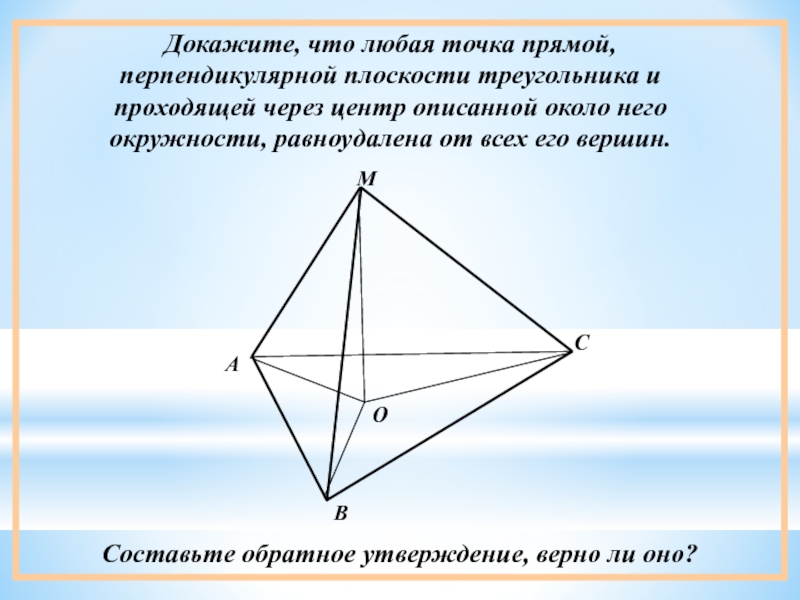
Слайд 14Докажите, что любая точка прямой, перпендикулярной плоскости треугольника и проходящей через
Составьте обратное утверждение, верно ли оно?
Слайд 15Назовите все наклонные к плоскости α
Назовите проекции этих наклонных на плоскость
Какой отрезок на чертеже определяет расстояние от точки М до плоскости α
ИТАК:
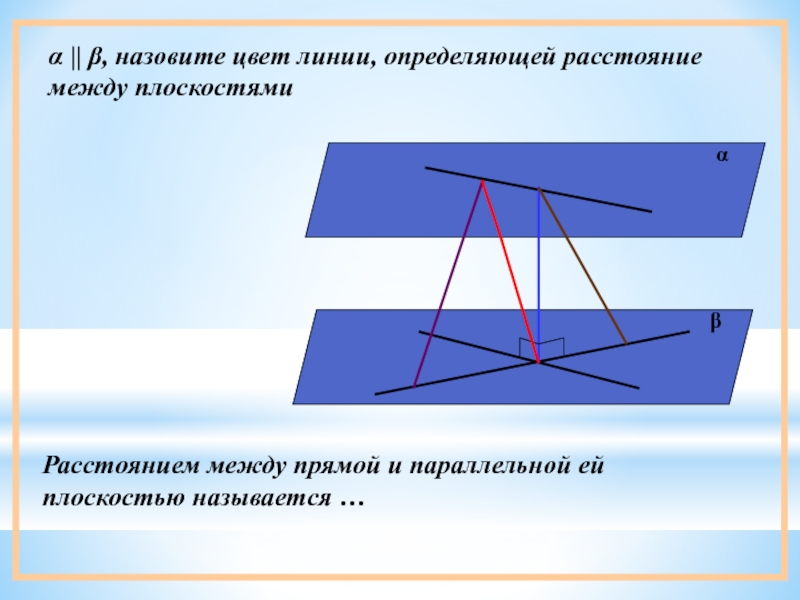
Слайд 16α || β, назовите цвет линии, определяющей расстояние между плоскостями
Расстоянием между