- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии Перпендикулярность плоскостей
Содержание
- 1. Презентация по геометрии Перпендикулярность плоскостей
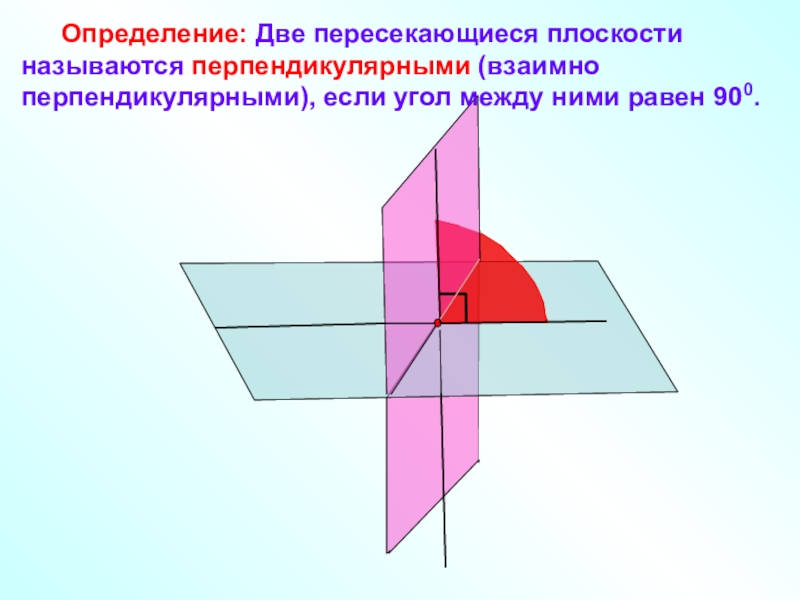
- 2. Определение: Две пересекающиеся плоскости называются перпендикулярными (взаимно перпендикулярными), если угол между ними равен 900.
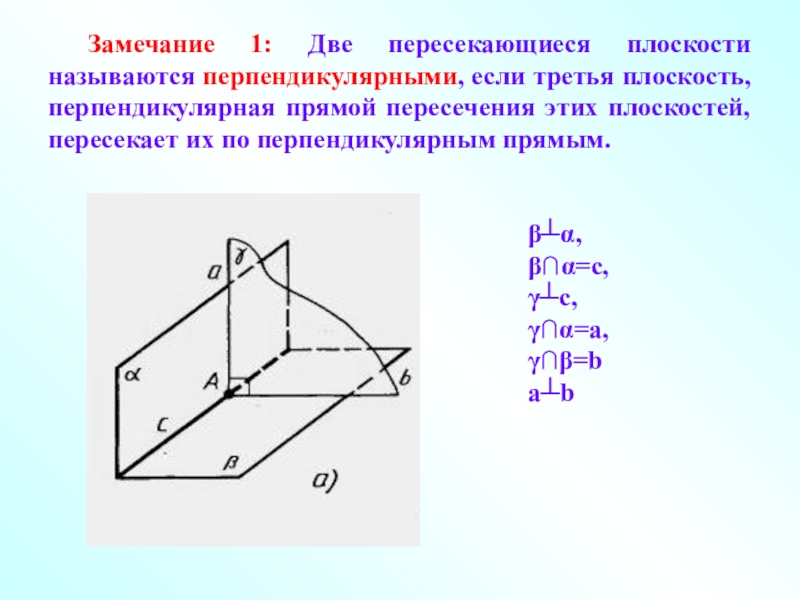
- 3. Замечание 1: Две пересекающиеся плоскости называются перпендикулярными,
- 4. Примером
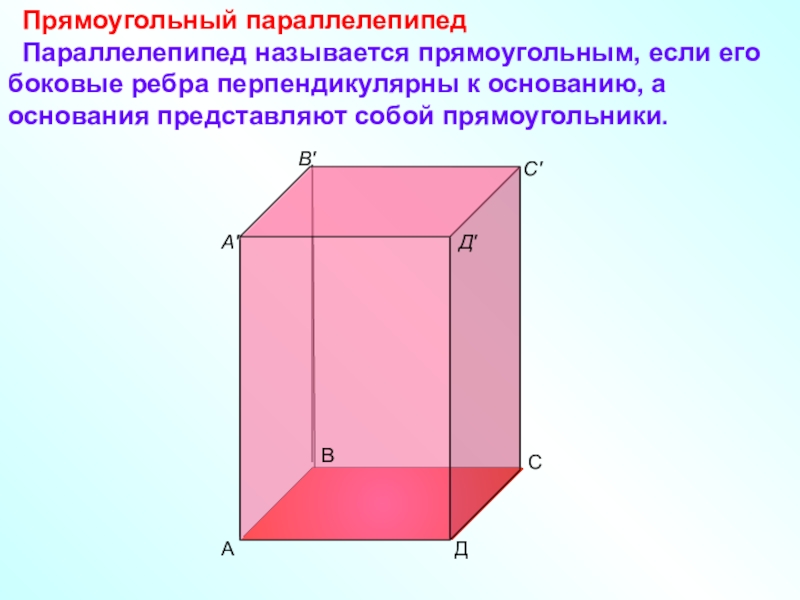
- 5. Прямоугольный параллелепипед
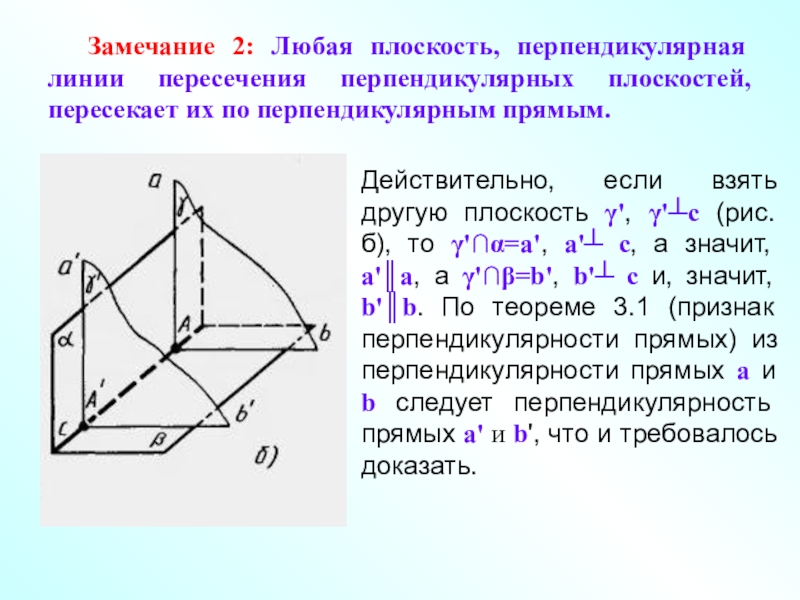
- 6. Замечание 2: Любая плоскость, перпендикулярная линии пересечения
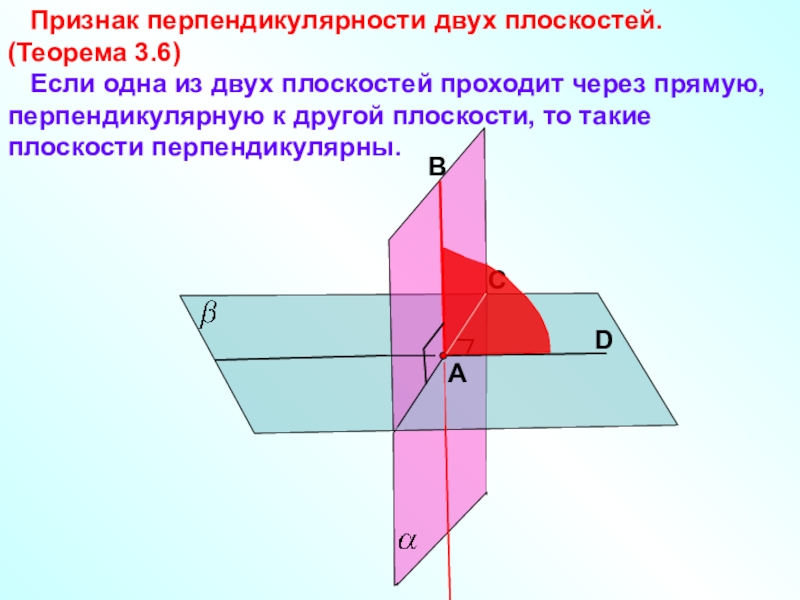
- 7. Признак перпендикулярности двух плоскостей. (Теорема
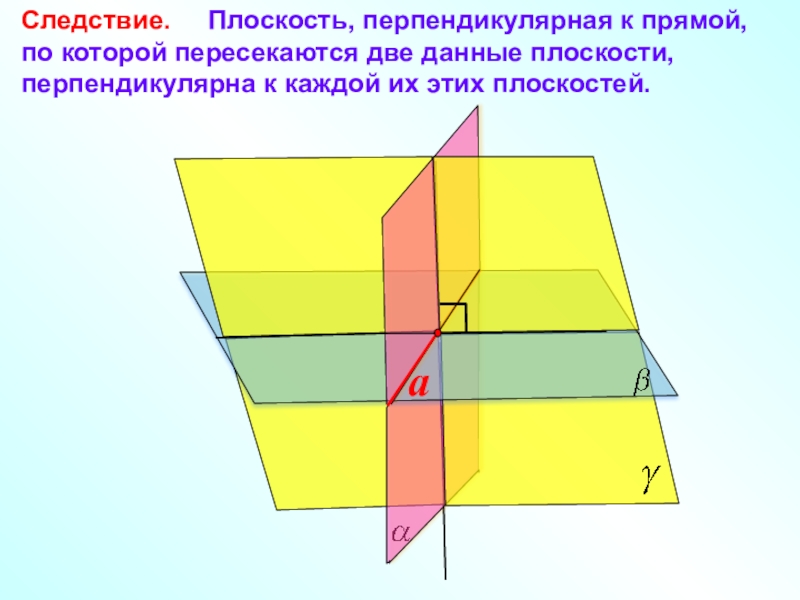
- 8. Следствие. Плоскость, перпендикулярная к прямой,
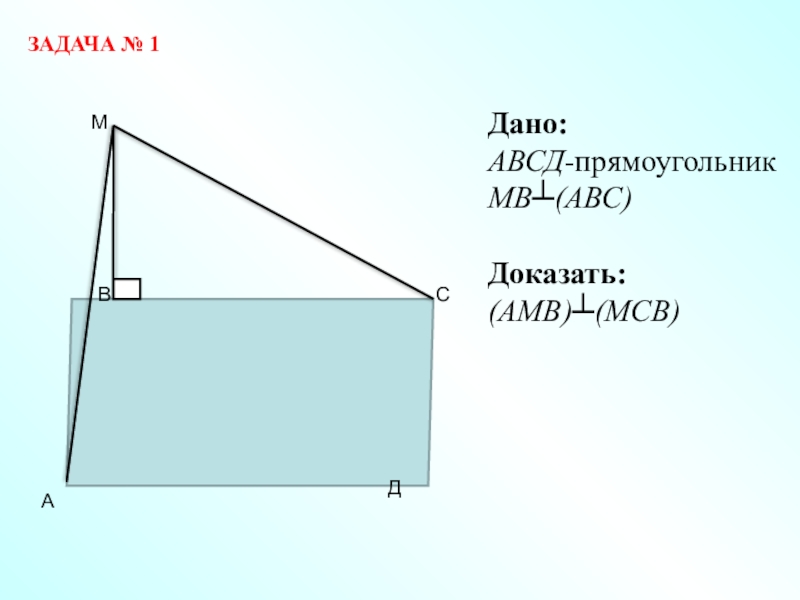
- 9. ЗАДАЧА № 1Дано: АВСД-прямоугольникМВ┴(АВС)Доказать:(АМВ)┴(МСВ)
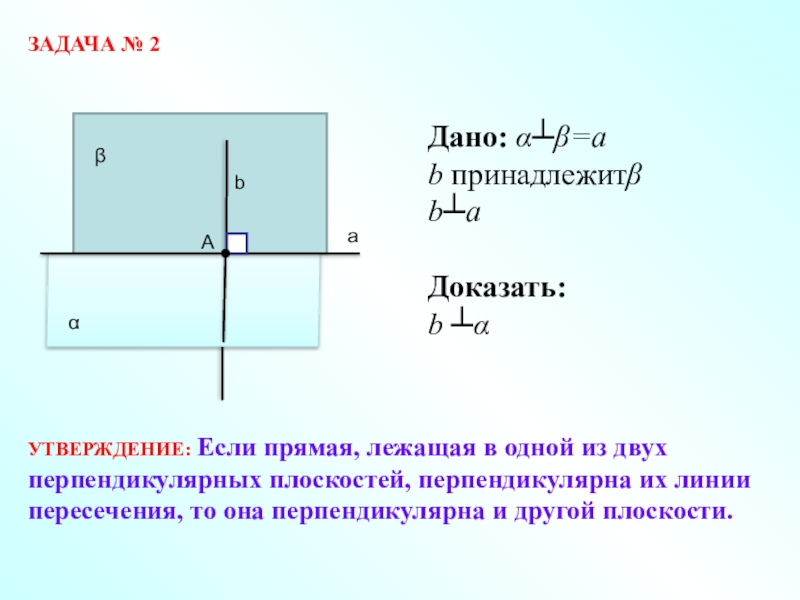
- 10. ЗАДАЧА № 2Дано: α┴β=аb принадлежитβb┴aДоказать:b ┴αУТВЕРЖДЕНИЕ: Если
- 11. № 59 Пункт 2.Дано: α┴β; А- принадлежит
Слайд 2
Определение: Две пересекающиеся плоскости называются перпендикулярными (взаимно перпендикулярными), если угол между
Слайд 3 Замечание 1: Две пересекающиеся плоскости называются перпендикулярными, если третья плоскость, перпендикулярная
β┴α,
β∩α=с,
γ┴с,
γ∩α=а,
γ∩β=b
a┴b
Слайд 4
Примером взаимно перпендикулярных плоскостей служат
плоскости стены и потолка.
Слайд 5 Прямоугольный параллелепипед
Параллелепипед называется прямоугольным,
Слайд 6 Замечание 2: Любая плоскость, перпендикулярная линии пересечения перпендикулярных плоскостей, пересекает их
Действительно, если взять другую плоскость γ', γ'┴с (рис. б), то γ'∩α=а', а'┴ с, а значит, а'║а, а γ'∩β=b', b'┴ с и, значит, b'║b. По теореме 3.1 (признак перпендикулярности прямых) из перпендикулярности прямых а и b следует перпендикулярность прямых а' и b', что и требовалось доказать.
Слайд 7
Признак перпендикулярности двух плоскостей. (Теорема 3.6)
Если одна из двух плоскостей проходит через прямую, перпендикулярную к другой плоскости, то такие плоскости перпендикулярны.
А
С
Слайд 8Следствие. Плоскость, перпендикулярная к прямой,
по которой пересекаются две
Слайд 10ЗАДАЧА № 2
Дано: α┴β=а
b принадлежитβ
b┴a
Доказать:
b ┴α
УТВЕРЖДЕНИЕ: Если прямая, лежащая в одной
перпендикулярных плоскостей, перпендикулярна их линии
пересечения, то она перпендикулярна и другой плоскости.
Слайд 11№ 59 Пункт 2.
Дано: α┴β; А- принадлежит α,
В – принадлежит
АС и ВД – перпендикуляры к прямой а;
АС = 3м, ВД = 4м, СД = 12м
Найти: длину отрезка АВ?
Решение: 1. Сделаем дополнительное построение проведем отрезки АВ и ВС. т.к. ВД┴а и АС ┴а (по условию), то ΔАСВ – прямоугольный. Тогда по теореме Пифагора следует, что
АВ2 = АС2 + ВС2.
2. Рассмотрим ΔВДС – прямоугольный. Тогда по теореме Пифагора ВС2 = ВД2 + СД2.
3. Т.О. получим ВС2 = 6+144 =160 м2;
АВ2 = 160 + 9 = 169; АВ =13м.
Ответ: 13м.