- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Пропорциональные отрезки
Содержание
- 1. Презентация по геометрии на тему Пропорциональные отрезки
- 2. Определение. Отрезки АВ и СD называются пропорциональными
- 3. Теорема о пропорциональных отрезках, отсекаемых параллельными прямыми
- 4. если на одной из двух прямых отложить
- 5. Теорема (обобщение теоремы Фалеса) Параллельные прямые, пересекающие две данные прямые, отсекают на этих прямых, пропорциональные отрезки.
- 6. Слайд 6
- 7. 2. Если стороны угла пересечены параллельными прямыми,
- 8. Задачи на нахождение отношений отрезков.Теорема. Биссектриса треугольника
- 9. Теорема. Если биссектриса внешнего угла при вершине
- 10. Задача. На биссектрисе BD треугольника АВС отмечена
- 11. Задача. На сторонах АС и ВС треугольника
- 12. Замечание. Существует простой способ, позволяющий запомнить полученные
- 13. Слайд 13
- 14. 6. Прямая, проходящая через вершину А треугольника
- 15. 1. Точка С делит отрезок АВ в
- 16. 3. Отрезок АВ=24см разделен в отношении 3:5.
- 17. 4. В трапеции ABCD боковые стороны AB
- 18. 5. На медиане BD треугольника ABC отмечена
- 19. 6. Прямая, проходящая через вершину А треугольника
- 20. Слайд 20
Слайд 1Пропорциональные отрезки
Учитель математики
МБОУ лицея №2
г. Южно – Сахалинска
Бокова Т.Н.
Фон лучше
Слайд 2
Определение. Отрезки АВ и СD называются пропорциональными
отрезкам А1В1 и С1D1,
Отрезки BC и AB пропорциональны отрезкам EF и FG, так как
коэффициент пропорциональности
Отрезки BC и AB не пропорциональны отрезкам EF и FM, так как
,
следовательно,
Слайд 3Теорема о пропорциональных отрезках, отсекаемых параллельными прямыми на сторонах угла.
Ели стороны
то отрезки OM и ON пропорциональны отрезкам OA и OB, то есть
Слайд 4если на одной из двух прямых отложить последовательно несколько равных отрезков
Напомним теорему Фалеса:
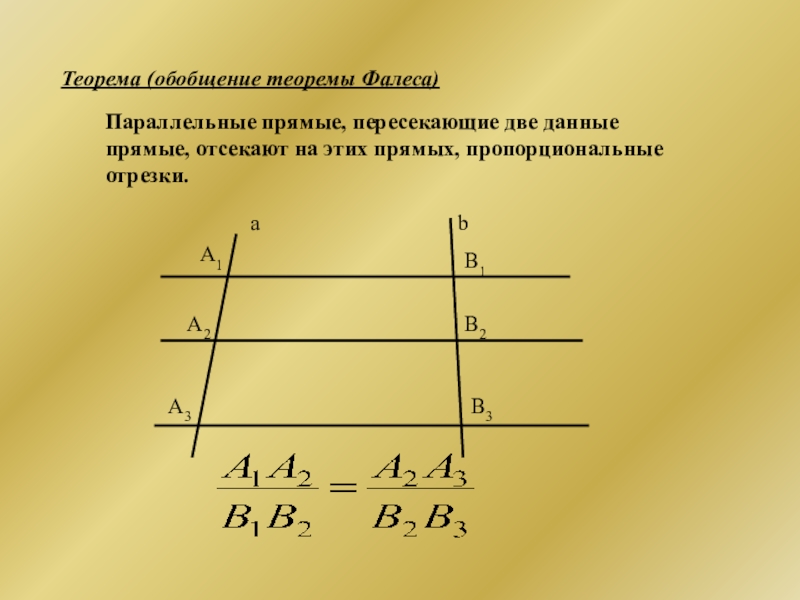
Слайд 5Теорема (обобщение теоремы Фалеса)
Параллельные прямые, пересекающие две данные прямые, отсекают
Слайд 6
Если стороны угла пересечены прямыми так, что полученные
отрезки на одной стороне пропорциональны
соответственным отрезкам на другой стороне, то секущие
прямые параллельны.
Слайд 72. Если стороны угла пересечены параллельными прямыми,
то отрезки параллельных
как отрезки, отсекаемые от сторон угла, считая от
вершины.
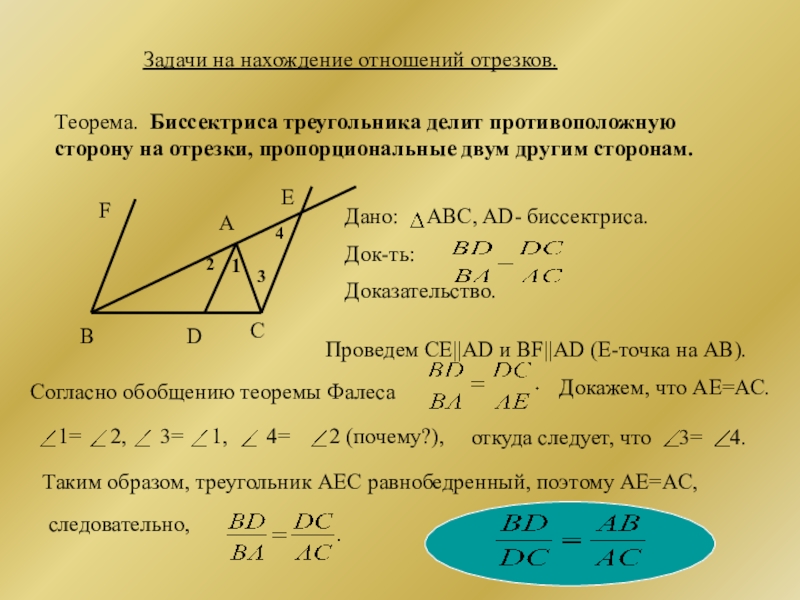
Слайд 8Задачи на нахождение отношений отрезков.
Теорема. Биссектриса треугольника делит противоположную сторону на
Дано: ABC, AD- биссектриса.
Док-ть:
Доказательство.
Проведем CE||AD и BF||AD (Е-точка на АВ).
Е
F
Согласно обобщению теоремы Фалеса
Докажем, что АЕ=АС.
1
2
3
4
1= 2, 3= 1, 4= 2 (почему?),
откуда следует, что 3= 4.
Таким образом, треугольник AEC равнобедренный, поэтому AE=AC,
следовательно,
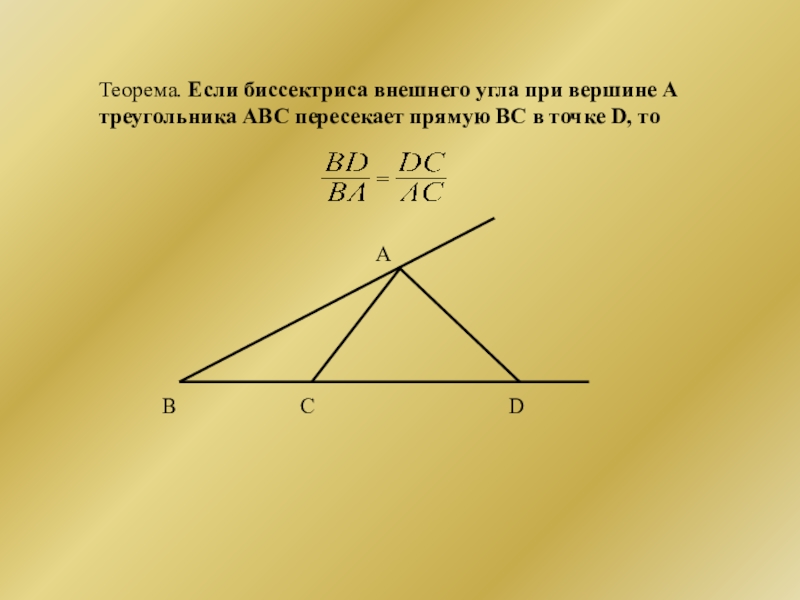
Слайд 9Теорема. Если биссектриса внешнего угла при вершине А треугольника АВС пересекает
В
А
С
D
Слайд 10Задача. На биссектрисе BD треугольника АВС отмечена точка М так, что
Проведем DP||AK.
P
По обобщению теоремы Фалеса отрезки BM и MD пропорциональны BK и KP, то есть
Точно так же отрезки AD и DC пропорциональны отрезкам KP и PC:
Но
Пусть КР=px тогда PC=qx, KC=(p+q)x, а из равенства (1) получаем
Откуда
Слайд 11Задача. На сторонах АС и ВС треугольника АВС отмечены точки К
Это утверждение называется теоремой о пропорциональных отрезках в треугольнике.
Задача решается аналогично предыдущей.
Слайд 12Замечание. Существует простой способ, позволяющий запомнить полученные формулы.
Например, чтобы написать формулу
и умножить его на отношение третьего отрезка к четвертому, сложенному с 1, то есть на
В результате получаем:
Формула для отношения ВО:ОК получается по тому же правилу, но нужно «двигаться» от то точки В к точке А:
Слайд 13
Точка С делит отрезок АВ в отношении АС:СВ=3:4.
Найти отношения:
Точка С делит отрезок АВ в отношении АС:СВ=m:n.
Найти отношения:
Отрезок АВ=24см разделен в отношении 3:5. Найти длины
полученных частей.
В трапеции ABCD боковые стороны AB и CD продолжены
до пересечения в точке F. Найти длину CD, если FB:BA=
=8:5 и FC-CD=2,25м.
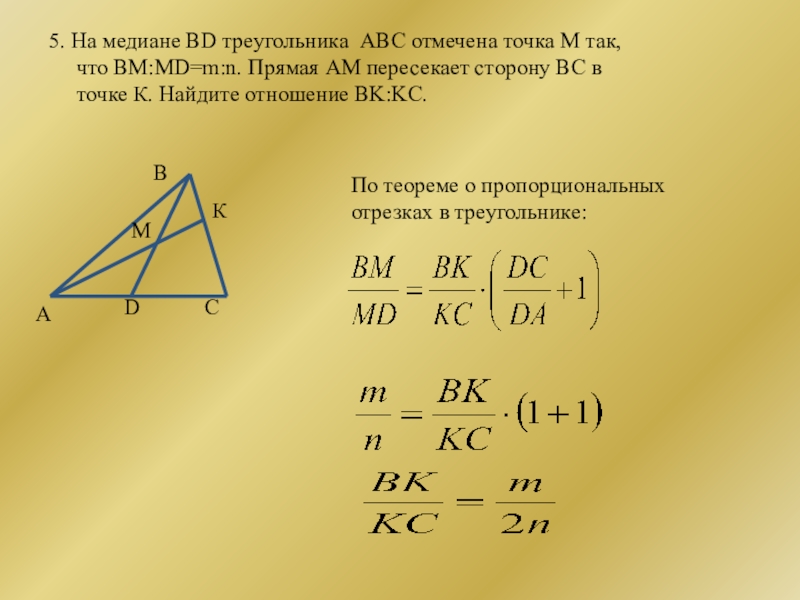
На медиане BD треугольника ABC отмечена точка М так,
что BM:MD=m:n. Прямая АМ пересекает сторону ВС в
точке К. Найдите отношение BK:KC.
Слайд 146. Прямая, проходящая через вершину А треугольника АВС и
пересекает сторону ВС в точке К. Найдите отношение
площадей треугольников ABК и ABC.
7. В треугольнике ABC медиана BM и биссектриса АК
пересекаются в точке О, АС:АВ=k. Найдите отношение
площадей треугольника AOB и четырехугольника MOKC.
Учебник: № 536, 537, 538, 539, 540
Слайд 15
1. Точка С делит отрезок АВ в отношении АС:СВ=3:4.
Найти
2. Точка С делит отрезок АВ в отношении АС:СВ=m:n.
Найти отношения:
Решения задач
Слайд 163. Отрезок АВ=24см разделен в отношении 3:5. Найти длины
Дано: АВ- отрезок, С АВ, АВ=24см,
АС:СВ=3:5.
Найти: АС, СВ.
Для решения на интерактивной доске.
Слайд 17
4. В трапеции ABCD боковые стороны AB и CD продолжены
FC-CD=2,25м.
Дано: АВСD-трапеция, АВ СD=F, FB:BA=8:5, FC-CD=2,25м
Найти:CD
Решение на интерактивной доске.
По теореме о пропорциональных отрезках:
Слайд 18
5. На медиане BD треугольника ABC отмечена точка М так,
точке К. Найдите отношение BK:KC.
По теореме о пропорциональных отрезках в треугольнике:
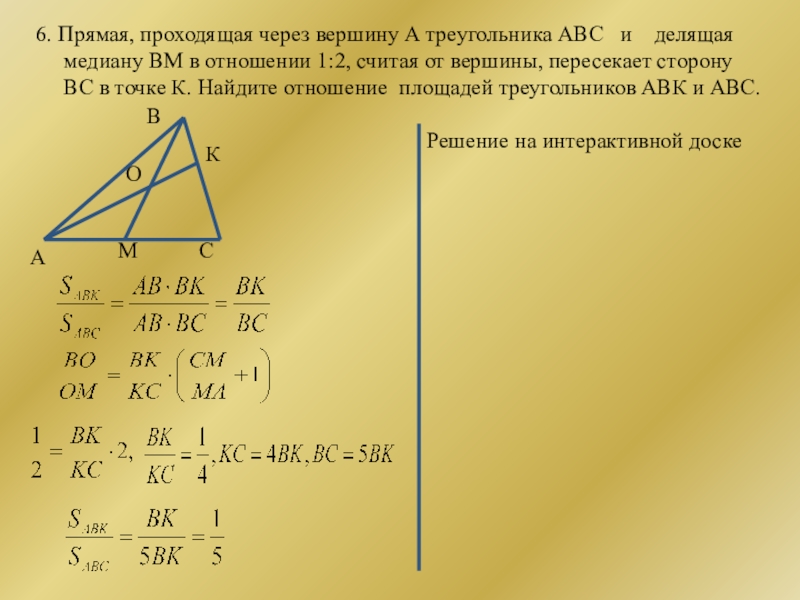
Слайд 196. Прямая, проходящая через вершину А треугольника АВС и
медиану BM в отношении 1:2, считая от вершины, пересекает сторону
ВС в точке К. Найдите отношение площадей треугольников ABК и ABC.
Решение на интерактивной доске
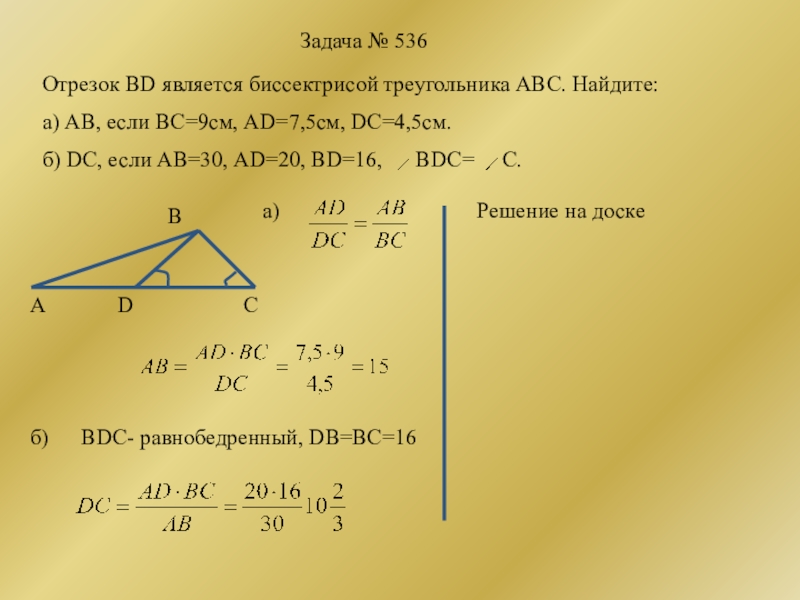
Слайд 20 Задача №
Отрезок BD является биссектрисой треугольника АВС. Найдите:
а) АВ, если ВС=9см, АD=7,5см, DC=4,5см.
б) DC, если АВ=30, АD=20, BD=16, BDC= C.
Решение на доске
а)
б) BDC- равнобедренный, DB=BC=16