- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Движение в пространстве(11 класс)
Содержание
- 1. Презентация по геометрии на тему Движение в пространстве(11 класс)
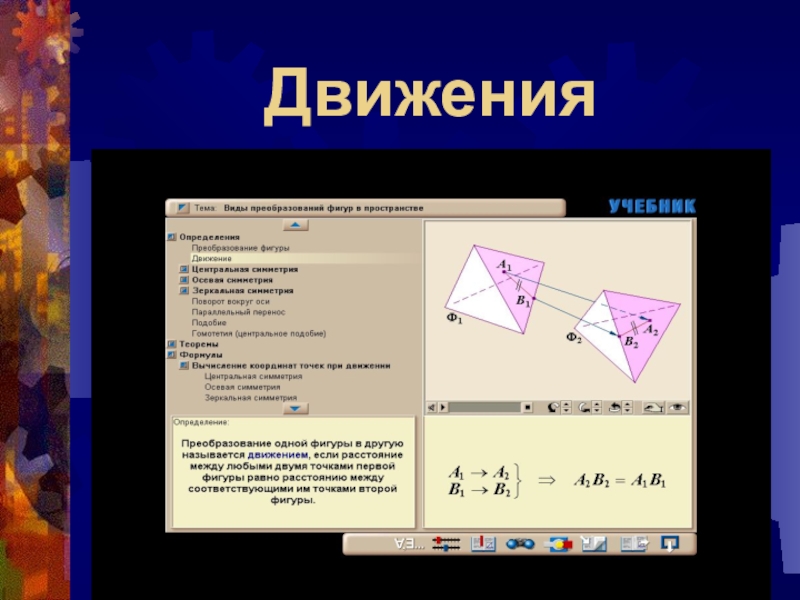
- 2. Движения
- 3. Преобразование симметрииВ древности слово «СИММЕТРИЯ» употреблялось в
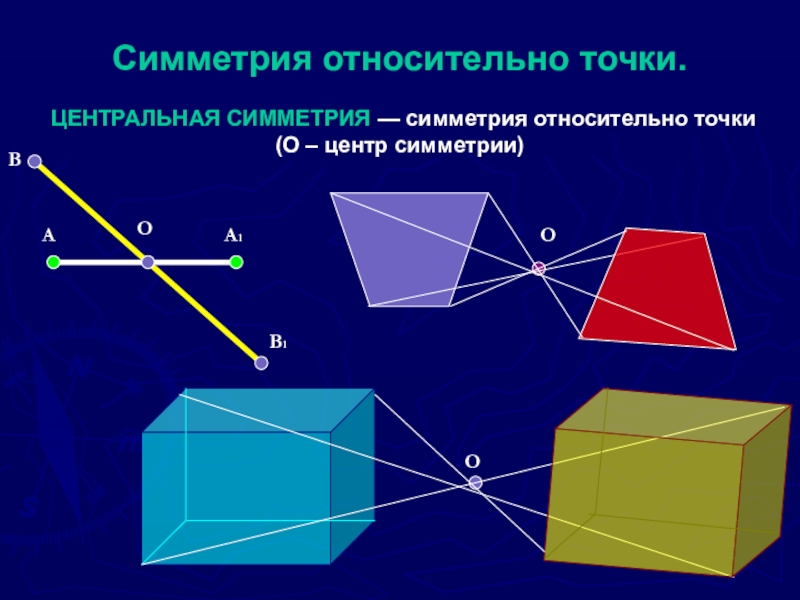
- 4. Симметрия относительно точки. ЦЕНТРАЛЬНАЯ СИММЕТРИЯ — симметрия относительно точки (О – центр симметрии)АА1ВВ1ООО
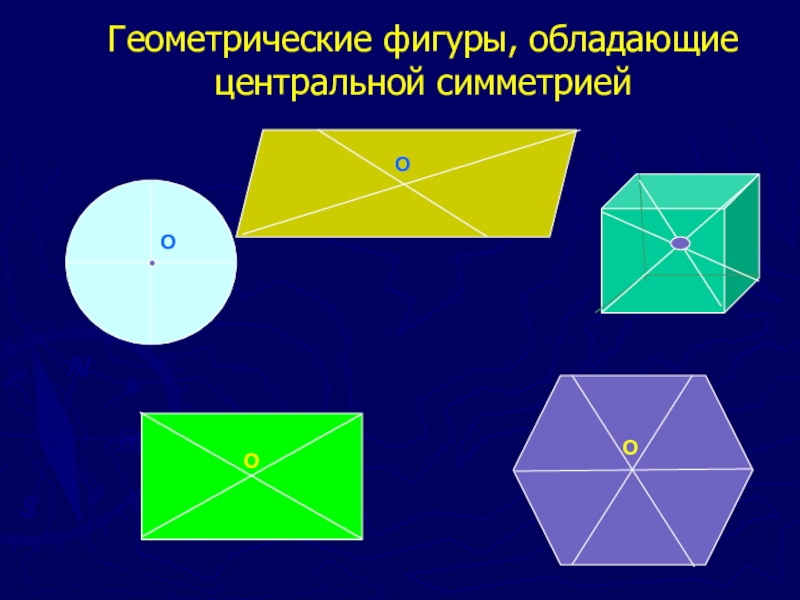
- 5. Геометрические фигуры, обладающие центральной симметриейОООО
- 6. Симметрия относительно точки –
- 7. Фигуры, обладающие центральной симметрией
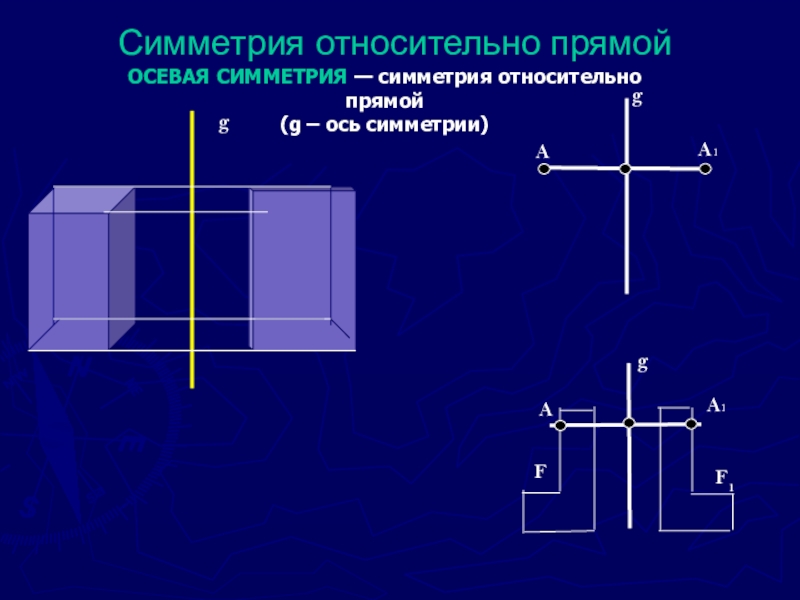
- 8. Симметрия относительно прямойgAA1gA1AFF1ОСЕВАЯ СИММЕТРИЯ — симметрия относительно прямой (g – ось симметрии)g
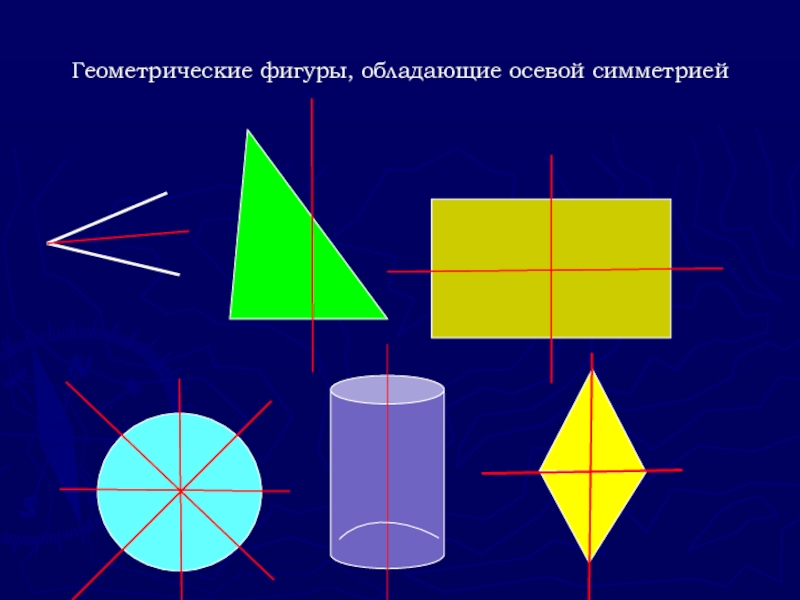
- 9. Геометрические фигуры, обладающие осевой симметрией
- 10. Осевая симметрия
- 11. Присмотритесь внимательно и вы увидите, что правая
- 12. Фигуры, обладающие осевой симметрией
- 13. Слайд 13
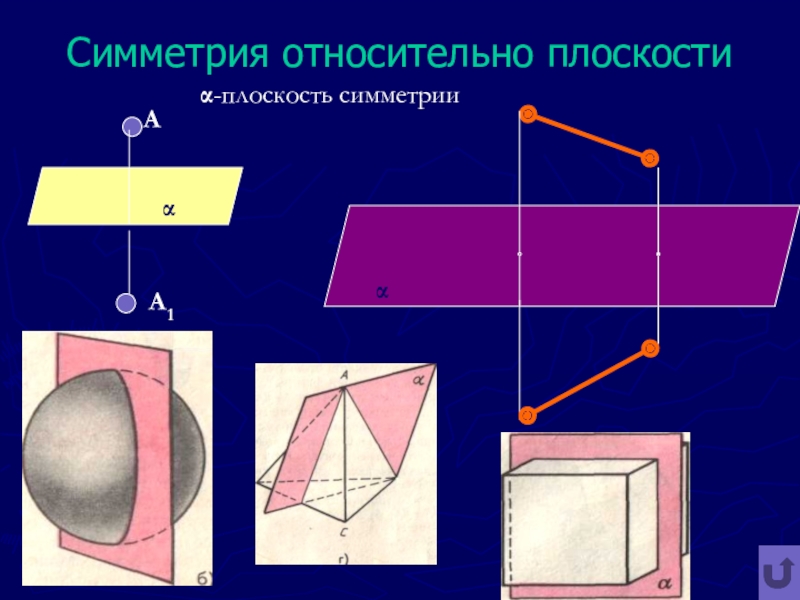
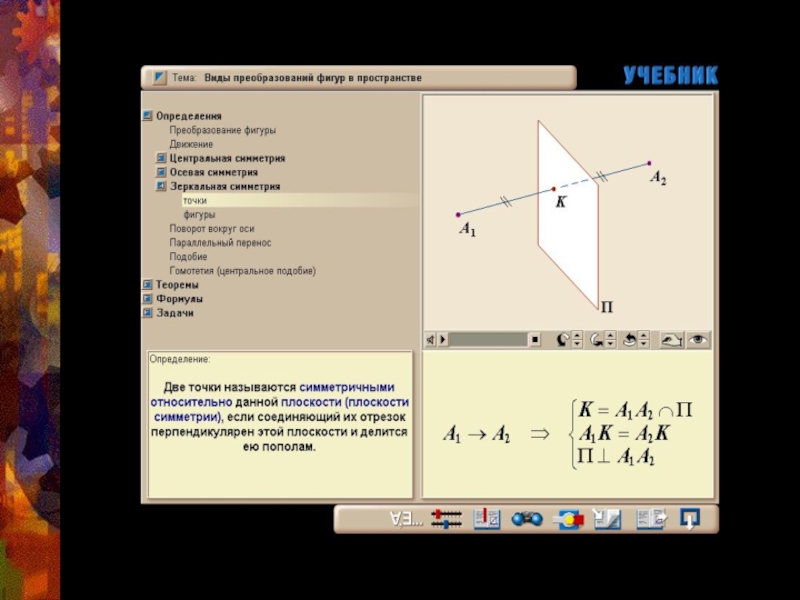
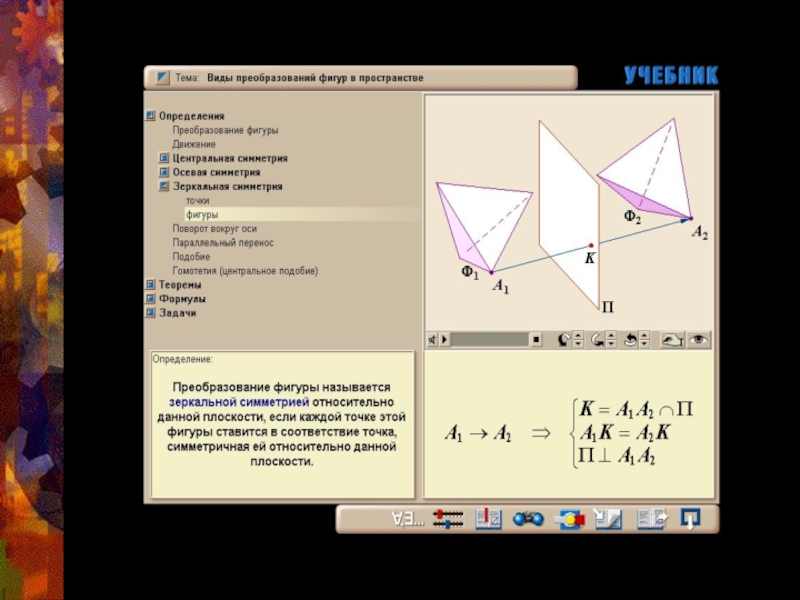
- 14. Симметрия относительно плоскостиАА1α-плоскость симметрииαα
- 15. Зеркальная симметрияФигура называется симметричной относительно плоскости, если
- 16. Слайд 16
- 17. Слайд 17
- 18. Замечательная постройка XVIII века – Казанский
- 19. В городе Осло, столице Норвегии, есть
- 20. Движение в пространстве:Симметрия относительно точки (центральная симметрия).
- 21. Симметрия относительно прямой (осевая симметрия)g
- 22. Симметрия относительно плоскости (зеркальная симметрия). α –
- 23. Поворотная симметрияЕсли n-число граней фигуры и n–натуральное
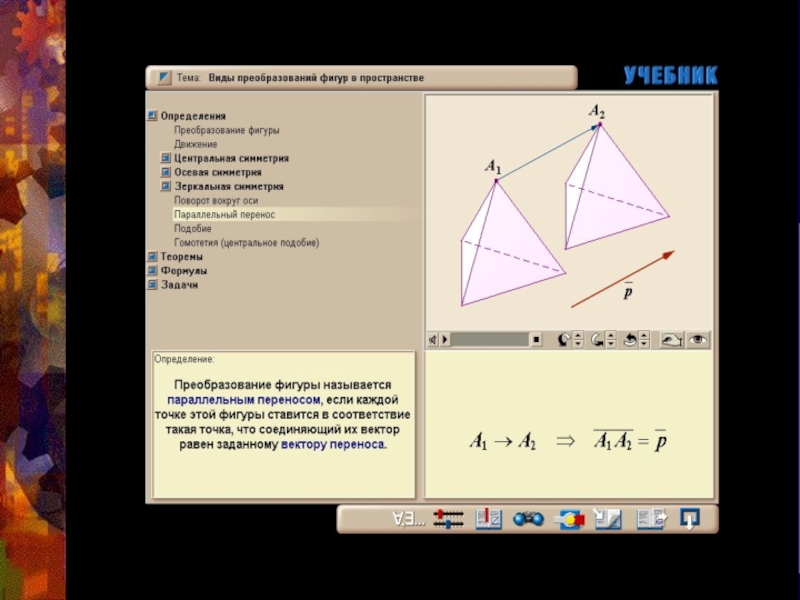
- 24. Параллельный переносПараллельным переносом на вектор р называют
- 25. Слайд 25
- 26. 11.10
- 27. Дополнительно:№1.Параллельный перенос задается формулами:х1=х+3 у1= у -
- 28. Сколько центров симметрии имеет:а)отрезок; б) прямая; в)
- 29. Д/з. выучить правила № 478(точки А и В)
Слайд 3Преобразование симметрии
В древности слово «СИММЕТРИЯ» употреблялось в значении «гармония», «красота». Действительно,
Слайд 4 Симметрия относительно точки. ЦЕНТРАЛЬНАЯ СИММЕТРИЯ — симметрия относительно точки (О – центр
А
А1
В
В1
О
О
О
Слайд 6Симметрия относительно точки – лучевая
Присмотритесь внимательно и вы увидите, что лепестки каждого тела расходятся во все стороны, как лучи от источника света. В математике - это симметрия относительно точки (центральная симметрия), в биологии – лучевая симметрия.
Слайд 8Симметрия относительно прямой
g
A
A1
g
A1
A
F
F1
ОСЕВАЯ СИММЕТРИЯ — симметрия относительно прямой
(g – ось
g
Слайд 11Присмотритесь внимательно и вы увидите, что правая сторона – есть зеркальное
Симметрия относительно прямой –
двусторонняя симметрия
Слайд 15Зеркальная симметрия
Фигура называется симметричной относительно плоскости, если преобразование симметрии переводит фигуру
При этом плоскость называется плоскостью симметрии этой фигуры.
Слайд 18 Замечательная постройка XVIII века – Казанский собор. Это архитектурный комплекс
Слайд 19 В городе Осло, столице Норвегии, есть выразительный ансамбль природы и
Слайд 20Движение в пространстве:
Симметрия относительно точки
(центральная симметрия).
О – центр
О(0;0;0) – центр симметрии
А(хА;уА;zA) B (хB;уB;zB) : хВ= - хА
уВ=- уА
zВ=- zА
Слайд 21Симметрия относительно прямой
(осевая симметрия)
g – ось симметрии
ОZ -
А(хА;уА;zA) B (хB;уB;zB) : хВ= - хА
уВ=- уА
zВ= zА
Слайд 22Симметрия относительно плоскости
(зеркальная симметрия).
α – плоскость симметрии
1. Оху –
А(хА;уА;zA) B (хB;уB;zB) : хВ= хА
уВ= уА
zВ= - zА
Слайд 23Поворотная симметрия
Если n-число граней фигуры и n–натуральное число больше1-го, то говорят,
При этом ось вращения называется осью поворотной симметрии порядка n.
Слайд 24Параллельный перенос
Параллельным переносом на вектор р называют отображение пространства на себя,
Слайд 26 11.10
№1. Дана точка А(1;2;3). Найдите координаты точки А1, симметричной точке А относительно начала координат.
№2. Точки А(5;-3;4) и В(-3;1;-2) симметричны относительно точки С. Найдите координаты точки С.
№3. Дана точка А(1;2;3). Найдите координаты точки, симметричной ей относительно оси: а) Ох; б) Оу; в) Оz.
№ 478(точка С)
Слайд 27Дополнительно:
№1.Параллельный перенос задается формулами:х1=х+3 у1= у - 3 ,z = z
№2.Параллельный перенос задается формулами: х1=х+1, у1 = у +2 , z1 = z+ 3 . Точка А при этом перенос переходит в точку В (2; 3; 1). Найдите координаты точки А.
№3. Точка А (1; 2; 3) при параллельном переносе переходит в точку В(3; 2; 1) . Запишите формулы этого параллельного переноса.
№4. Существует ли параллельный перенос, при котором точка А (1; 3; 2) переходит в точку В(0; 2; 4) , а точка D(2; 2; 2) переходит в точку С(1; 1; 4)?
Слайд 28Сколько центров симметрии имеет:
а)отрезок; б) прямая; в) окружность;
Сколько осей симметрии имеет:
а)отрезок; б) прямая; в) окружность; г) плоскость; д) куб?
Сколько плоскостей симметрии имеет:
а)отрезок; б) прямая; в) окружность; г) плоскость; д) куб?