- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии для 9 класса по теме Движения
Содержание
- 1. Презентация по геометрии для 9 класса по теме Движения
- 2. Введение: 1.Понятие движения. * Отображение плоскости на
- 3. История симметрииОднако как люди дошли до такой
- 4. Роль симметрии в миреА собственно, как бы
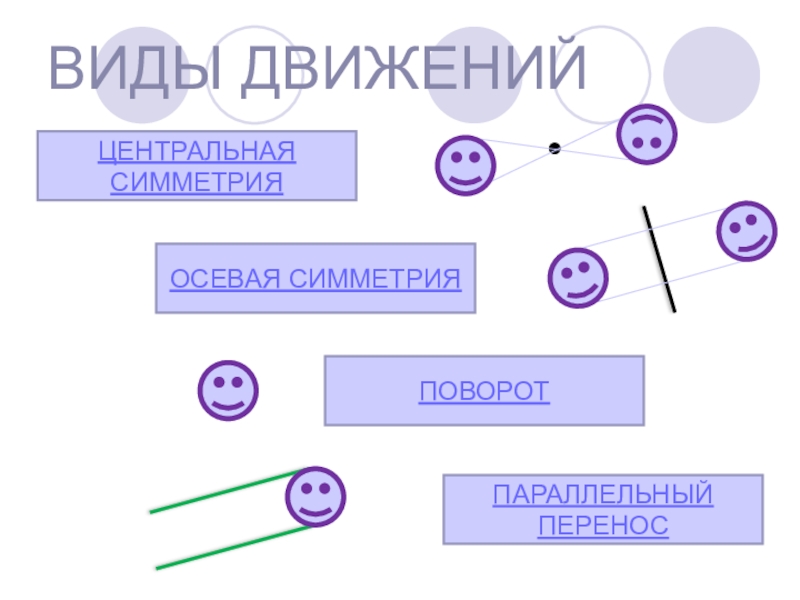
- 5. ВИДЫ ДВИЖЕНИЙОСЕВАЯ СИММЕТРИЯЦЕНТРАЛЬНАЯ СИММЕТРИЯПОВОРОТПАРАЛЛЕЛЬНЫЙ ПЕРЕНОС
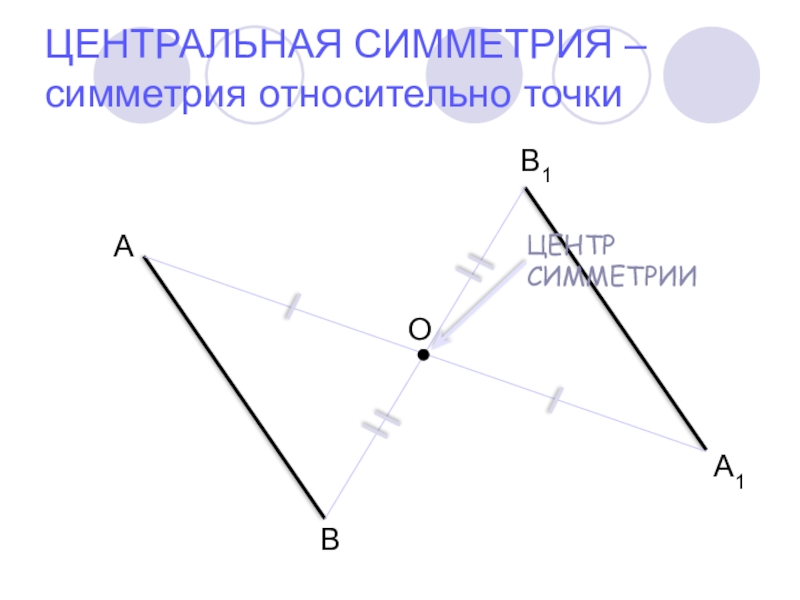
- 6. ЦЕНТРАЛЬНАЯ СИММЕТРИЯ – симметрия относительно точкиА1АВВ1О
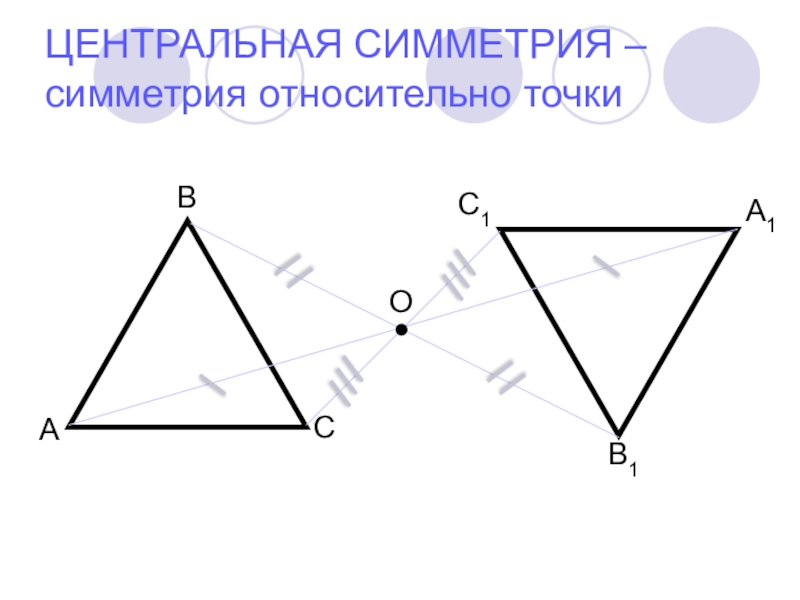
- 7. ОА1В1С1ЦЕНТРАЛЬНАЯ СИММЕТРИЯ – симметрия относительно точки
- 8. чтобы построить фигуру, симметричную данной
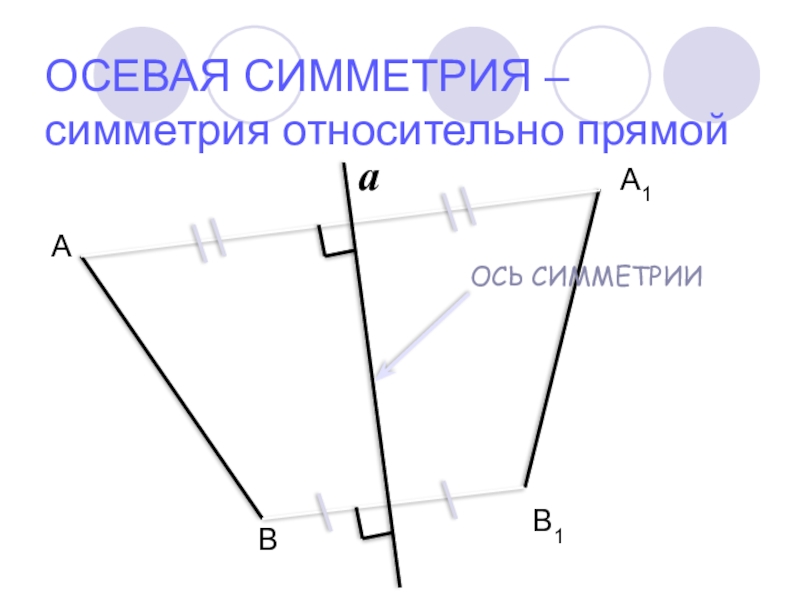
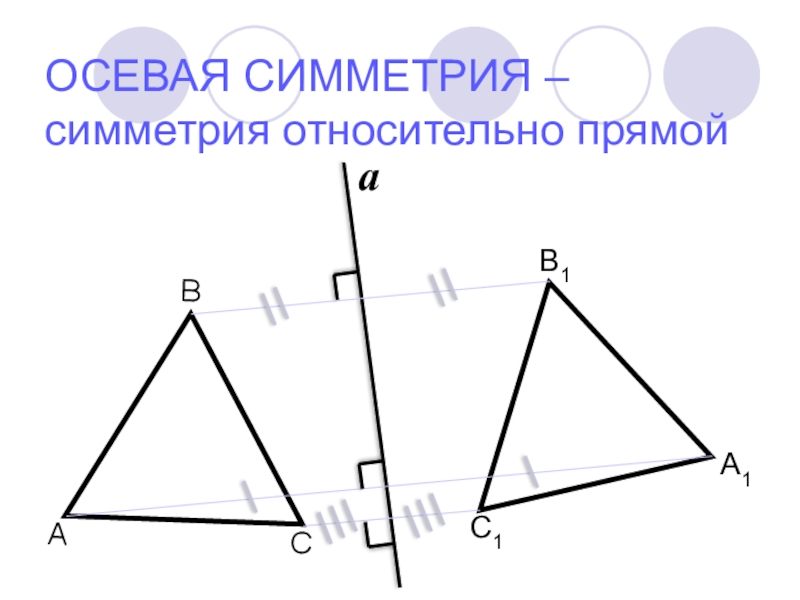
- 9. ОСЕВАЯ СИММЕТРИЯ – симметрия относительно прямой АВА1В1a
- 10. ОСЕВАЯ СИММЕТРИЯ – симметрия относительно прямой С1А1В1a
- 11. чтобы построить фигуру, симметричную данной
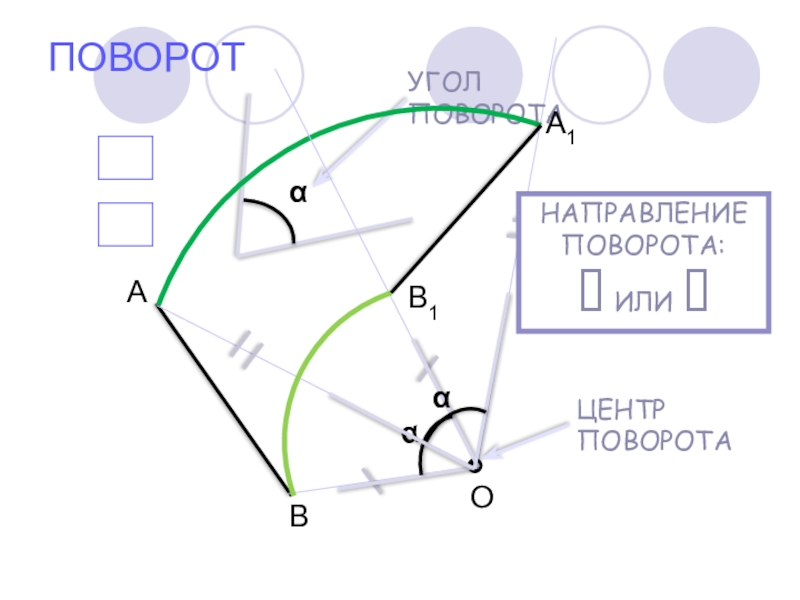
- 12. ПОВОРОТОАВА1В1НАПРАВЛЕНИЕ ПОВОРОТА:? ИЛИ ⮷?
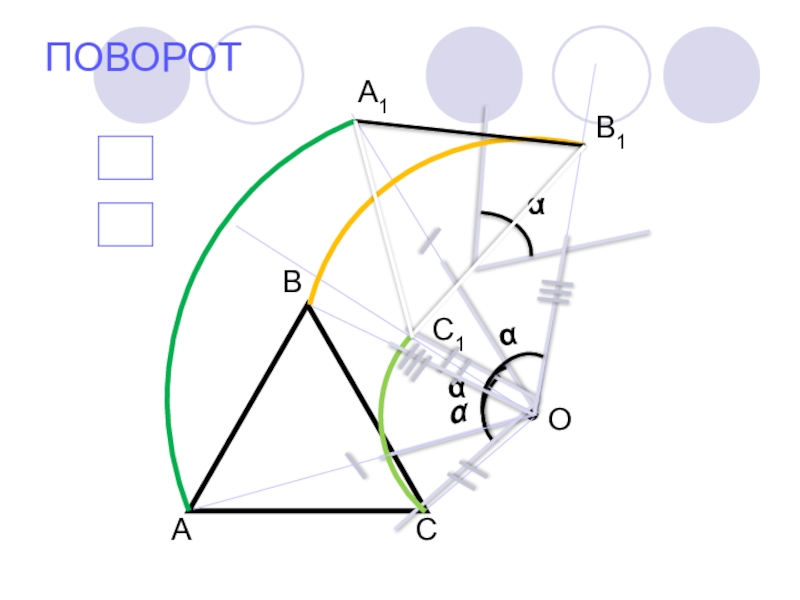
- 13. ПОВОРОТОА1В1С1?
- 14. ПОВОРОТ Сделаем вывод:Чтобы получить отображение фигуры при
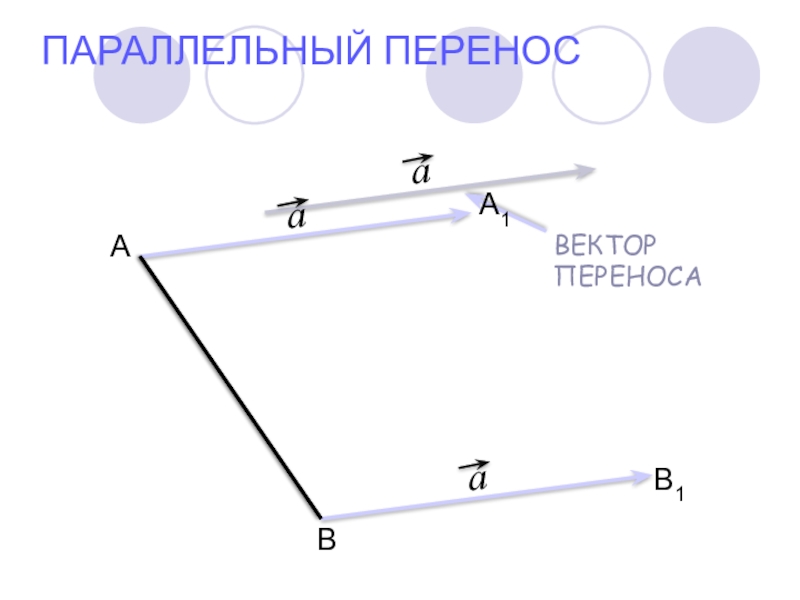
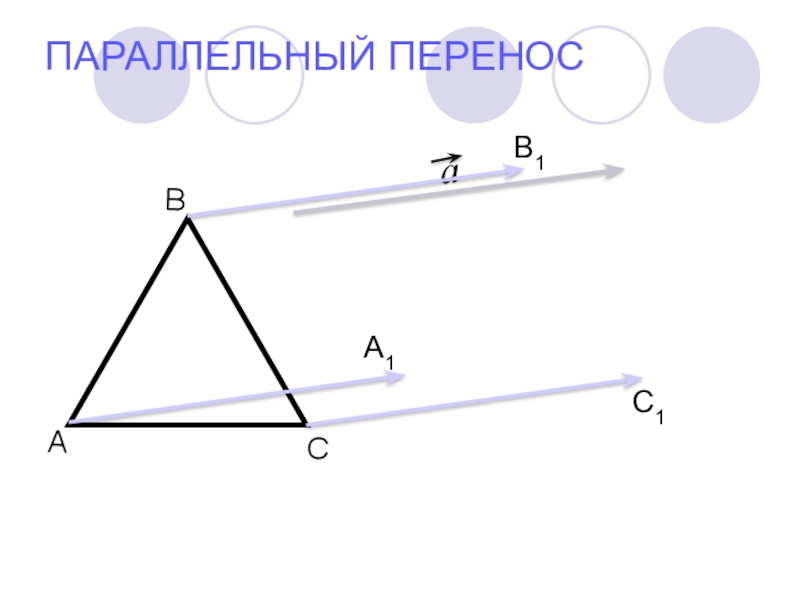
- 15. ПАРАЛЛЕЛЬНЫЙ ПЕРЕНОСАВА1В1
- 16. ПАРАЛЛЕЛЬНЫЙ ПЕРЕНОСС1А1В1САВ
- 17. ПАРАЛЛЕЛЬНЫЙ ПЕРЕНОС Сделаем вывод:Чтобы отобразить фигуру с
- 18. СВОЙСТВА ДВИЖЕНИЯПри движении прямые переходят в прямые,
- 19. Любая фигура переходит в равную ей фигуру
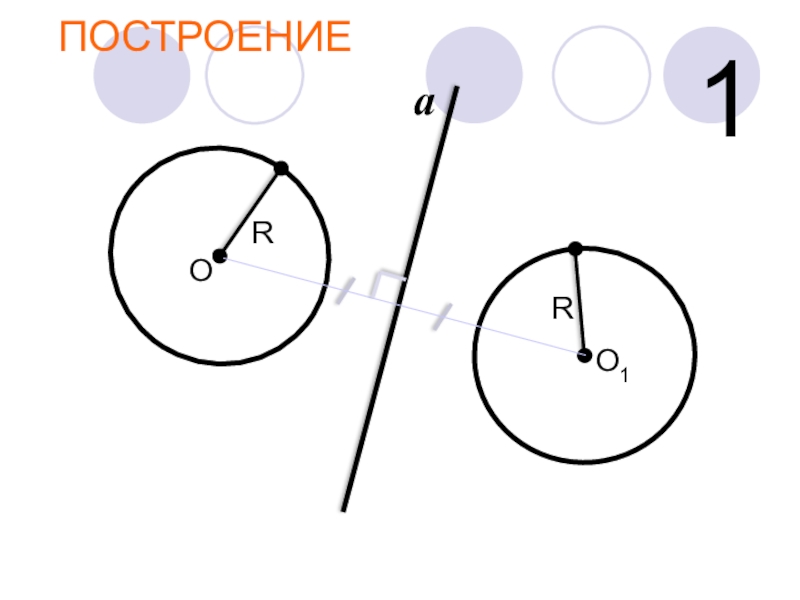
- 20. ЗАДАЧИ 1. Постройте окружность, симметричную данной относительно
- 21. ПОСТРОЕНИЕОa1О1RR
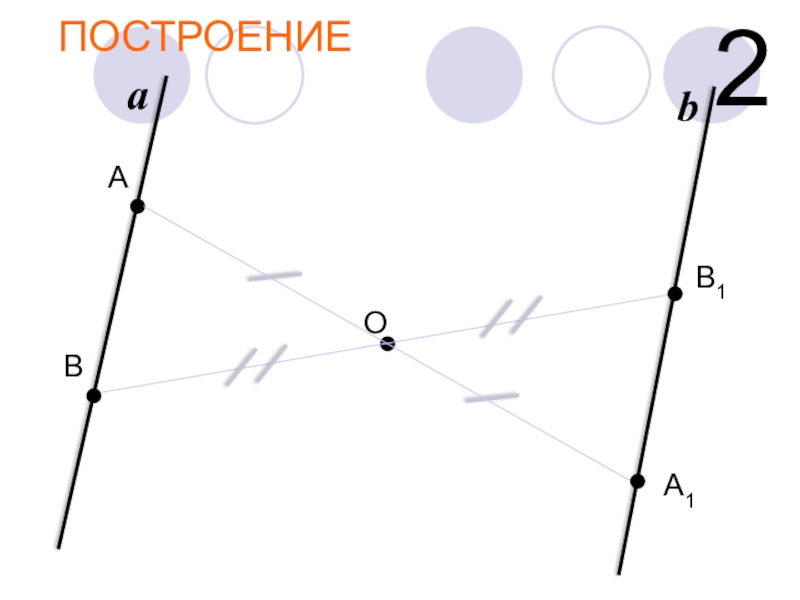
- 22. ЗАДАЧИ 2. Постройте прямую, симметричную данной относительно
- 23. ПОСТРОЕНИЕОa2АА1В1bВ
- 24. Выводы:Движение и все его виды очень важны
Введение: 1.Понятие движения. * Отображение плоскости на себя. *Наложения и движения. 2.Параллельный перенос и поворот. *Параллельный перенос. *Поворот.
Слайд 1Геометрия 9 класс
Тема «Движения»
город Курган
МБОУ «Лицей №12»
Выполнила ученица 9Б класса
Спиридонова Виктория
Слайд 2Введение:
1.Понятие движения.
* Отображение плоскости на себя.
*Наложения и движения.
2.Параллельный перенос и
поворот.
*Параллельный перенос.
*Поворот.
Слайд 3История симметрии
Однако как люди дошли до такой сложной и одновременно такой
простой вещи, как симметрия?
Ещё древние греки считали, что симметрия – это гармония, соразмерность. Они же и ввели термин συμμετρία, который сейчас перешёл в русское слово «симметрия»
А у древних народов, таких как шумеры и египтяне, у первобытных племён, да и у кое-кого в наше время симметрия ассоциируется не только с красотой и гармонией, но и прежде всего с магией. Не зря же люди в эпоху мегалита для ритуальных целей сооружали кромлихи в форме круга – «идеально симметричной» геометрической фигуры.
Ещё древние греки считали, что симметрия – это гармония, соразмерность. Они же и ввели термин συμμετρία, который сейчас перешёл в русское слово «симметрия»
А у древних народов, таких как шумеры и египтяне, у первобытных племён, да и у кое-кого в наше время симметрия ассоциируется не только с красотой и гармонией, но и прежде всего с магией. Не зря же люди в эпоху мегалита для ритуальных целей сооружали кромлихи в форме круга – «идеально симметричной» геометрической фигуры.
Слайд 4Роль симметрии в мире
А собственно, как бы нам жилось без симметрии?
Точнее, какую роль играет симметрия в нашем мире? Неужели она лишь украшает его? Оказывается, что без симметрии наш мир выглядел бы совсем по-другому. Ведь это именно на симметрии основаны многие законы сохранения. Например, законы сохранения энергии, импульса и момента импульса являются следствиями пространственно-временных симметрий, которые являются, как математическими, так и физическими симметриями. И без этих симметрий не было бы законов сохранений, которые во многом управляют нашим миром. Так что симметрия – пожалуй, чуть ли не самая главная вещь во Вселенной.
Слайд 8 чтобы построить фигуру, симметричную данной относительно точки О, нужно каждую точку
фигуры соединить с точкой О, продолжить полученный отрезок равным ему, отметить на конце этого отрезка образ исходной точки, затем соединить полученные образы
ЦЕНТРАЛЬНАЯ СИММЕТРИЯ – симметрия относительно точки
Сделаем вывод:
Пример из жизни
Слайд 11 чтобы построить фигуру, симметричную данной относительно прямой а, нужно из каждой
точки фигуры провести перпендикуляр к прямой а, продолжить полученный отрезок равным ему, отметить на конце этого отрезка образ исходной точки, затем соединить полученные образы
ОСЕВАЯ СИММЕТРИЯ –
симметрия относительно прямой
Сделаем вывод:
Пример из жизни
Слайд 14ПОВОРОТ
Сделаем вывод:
Чтобы получить отображение фигуры при повороте около данной точки, нужно
каждую точку фигуры повернуть на один и тот же угол в одном и том же направлении (по часовой стрелке или против часовой стрелки)
Слайд 17ПАРАЛЛЕЛЬНЫЙ ПЕРЕНОС
Сделаем вывод:
Чтобы отобразить фигуру с помощью параллельного переноса, нужно каждую
точку фигуры переместить на заданный вектор, а затем соединить полученные образы
Слайд 18СВОЙСТВА ДВИЖЕНИЯ
При движении прямые переходят в прямые, полупрямые – в полупрямые,
отрезки – в отрезки.
Точки, лежащие на прямой, переходят в точки, лежащие на прямой, и сохраняется порядок их взаимного расположения.
Сохраняются углы между полупрямыми. ЗНАЧИТ…
Точки, лежащие на прямой, переходят в точки, лежащие на прямой, и сохраняется порядок их взаимного расположения.
Сохраняются углы между полупрямыми. ЗНАЧИТ…
Слайд 20ЗАДАЧИ
1. Постройте окружность, симметричную данной относительно заданной прямой.
Решение:
для построения любой
окружности нужно знать её центр и радиус.
Поэтому, для построения окружности, симметричной данной, нужно :
построить точку, симметричную центру;
измерить радиус исходной окружности;
этим же радиусом построить окружность с центром в симметричной точке.
Поэтому, для построения окружности, симметричной данной, нужно :
построить точку, симметричную центру;
измерить радиус исходной окружности;
этим же радиусом построить окружность с центром в симметричной точке.
ПОСТРОЕНИЕ
Слайд 22ЗАДАЧИ
2. Постройте прямую, симметричную данной относительно заданной точки.
Решение:
Мы знаем, что
через две точки можно провести прямую и притом только одну.
Поэтому, для построения прямой, симметричной данной, нужно :
произвольно выбрать две точки на данной прямой;
построить симметричные им точки;
через полученные точки провести прямую – это и будет искомая прямая.
Поэтому, для построения прямой, симметричной данной, нужно :
произвольно выбрать две точки на данной прямой;
построить симметричные им точки;
через полученные точки провести прямую – это и будет искомая прямая.
ПОСТРОЕНИЕ
Слайд 24Выводы:
Движение и все его виды очень важны в нашей жизни. Без
них не было бы тех архитектурных сооружений и технических достижений, что мы имеем.