- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии 11 класс Простейшие задачи в координатах
Содержание
- 1. Презентация по геометрии 11 класс Простейшие задачи в координатах
- 2. Из точки А(6; 8) опущены перпендикуляры на
- 3. 3) Найдите расстояние от точки A с координатами (6;
- 4. 5) Найдите абсциссу точки, симметричной точке A(6; 8) относительно оси Oy.В(-6; 8)Ответ: -6
- 5. 6) Найдите ординату точки, симметричной точке A(6; 8) относительно оси Ox.Ответ: -8
- 6. 7) Найдите ординату точки, симметричной точке A(6; 8) относительно начала координат.В(-6; - 8)Ответ: -8
- 7. Вычисление координат середины отрезка.Вычисление длины отрезка по его координатам.Сегодня на уроке:Вычисление расстояния между двумя точками.
- 8. 1. Определение координат середины отрезкаКаждая координата середины отрезкаравна полусуммесоответствующих координат его концов.
- 9. Найдите абсциссу середины отрезка, соединяющего точки O(0,
- 10. Найдите абсциссу середины отрезка, соединяющего точки A(6; 8)
- 11. Слайд 11
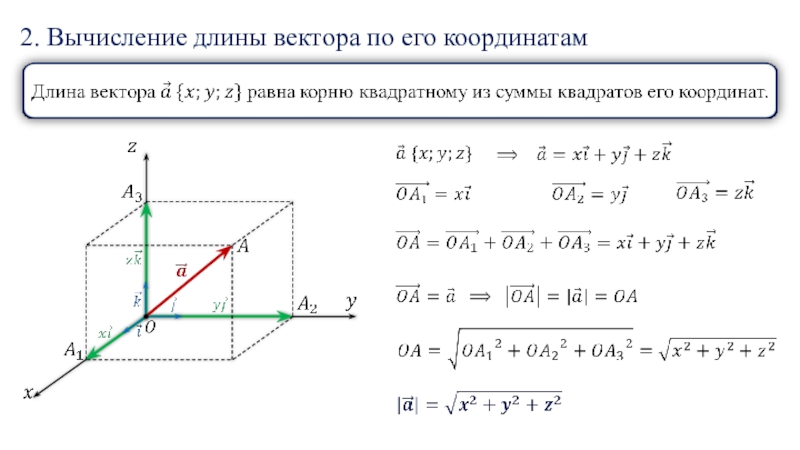
- 12. 2. Вычисление длины вектора по его координатам
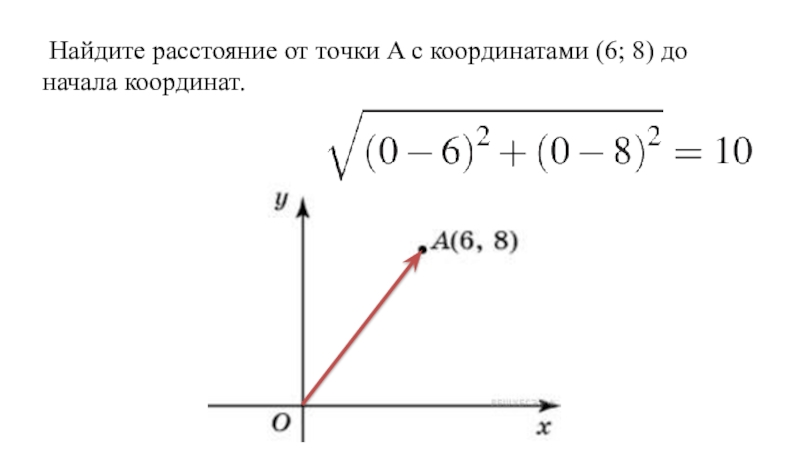
- 13. Найдите расстояние от точки A с координатами (6; 8) до начала координат.
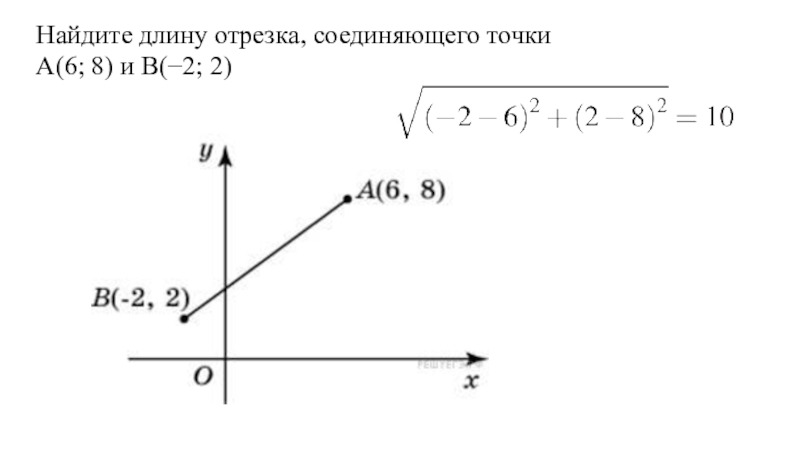
- 14. Найдите длину отрезка, соединяющего точки A(6; 8) и В(−2; 2)
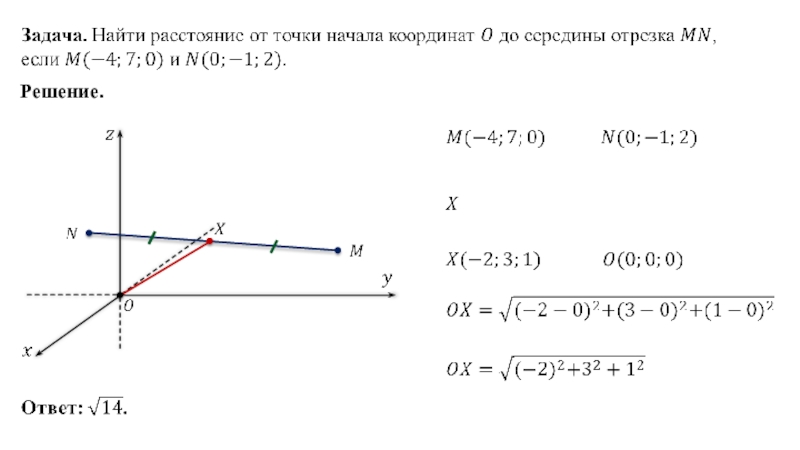
- 15. Решение.
- 16. Решение.
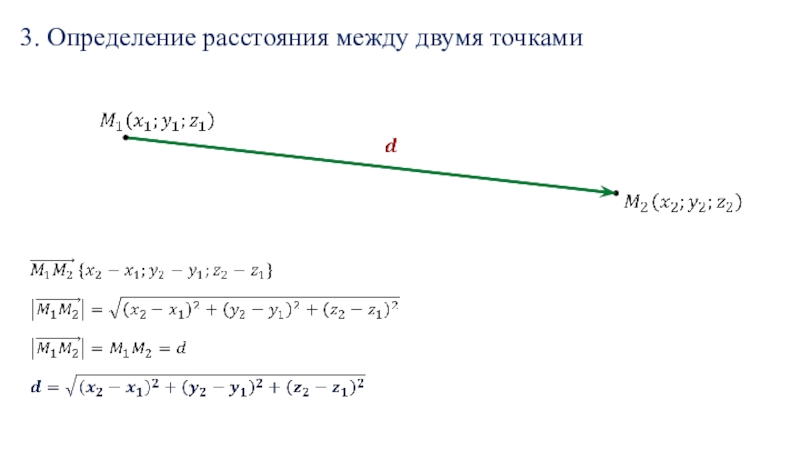
- 17. 3. Определение расстояния между двумя точками
- 18. Решение.
- 19. Решение.
- 20. Решение.
- 21. Слайд 21
- 22. Домашнее задание: №426, 424( а)
Из точки А(6; 8) опущены перпендикуляры на ось абсцисс, ординат. 1) Найдите абсциссу основания перпендикуляра. 2) Найдите ординату ее точки пересечения с осью Oy. Готовимся к ЕГЭ.(базовый)68
Слайд 2 Из точки А(6; 8) опущены перпендикуляры на ось абсцисс, ординат.
1)
Найдите абсциссу основания перпендикуляра.
2) Найдите ординату ее точки пересечения с осью Oy.
2) Найдите ординату ее точки пересечения с осью Oy.
Готовимся к ЕГЭ.(базовый)
6
8
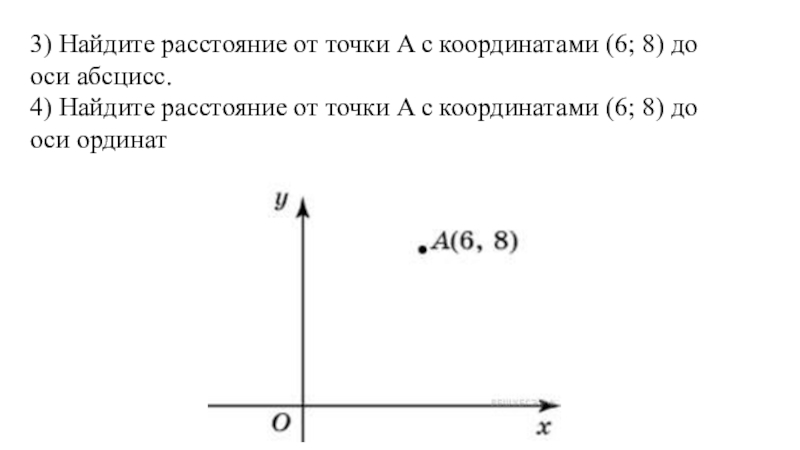
Слайд 33) Найдите расстояние от точки A с координатами (6; 8) до оси абсцисс.
4)
Найдите расстояние от точки A с координатами (6; 8) до оси ординат
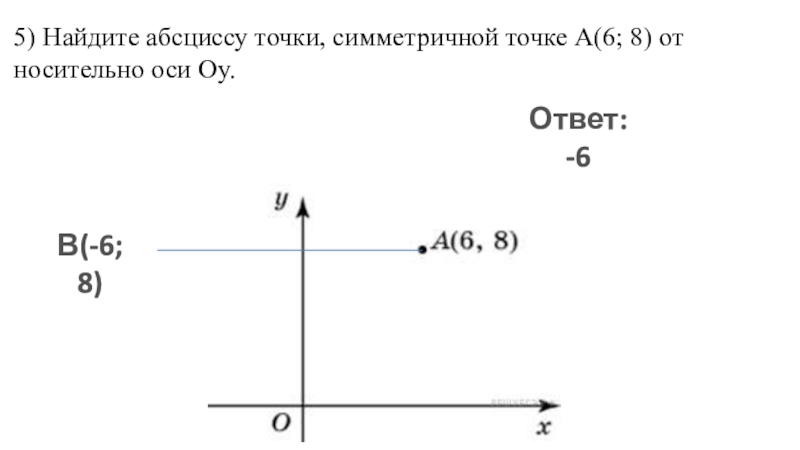
Слайд 45) Найдите абсциссу точки, симметричной точке A(6; 8) относительно оси Oy.
В(-6; 8)
Ответ: -6
Слайд 56) Найдите ординату точки, симметричной точке A(6; 8) относительно оси Ox.
Ответ: -8
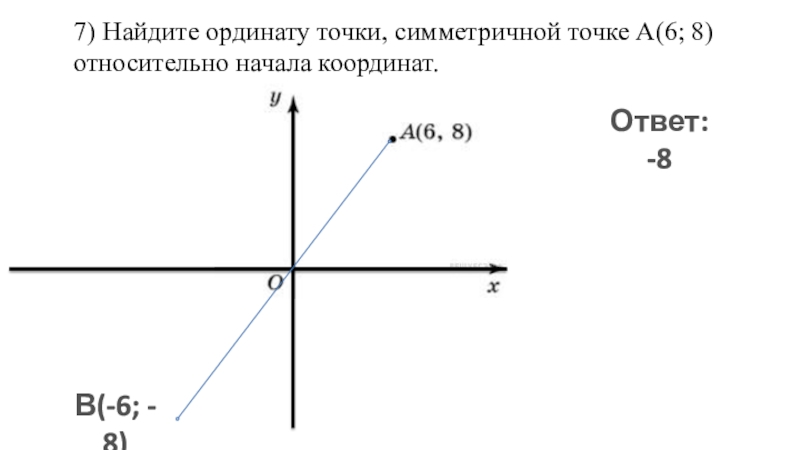
Слайд 67) Найдите ординату точки, симметричной точке A(6; 8) относительно начала координат.
В(-6; -
8)
Ответ: -8
Слайд 7Вычисление координат середины отрезка.
Вычисление длины отрезка по его координатам.
Сегодня на уроке:
Вычисление
расстояния между двумя точками.
Слайд 81. Определение координат середины отрезка
Каждая координата середины отрезка
равна полусумме
соответствующих координат его
концов.
Слайд 9Найдите абсциссу середины отрезка, соединяющего точки O(0, 0) и A(6, 8).
Найдите ординату
середины отрезка, соединяющего точки O(0; 0) и A (6; 8)
Ответ: 4
Ответ: 3
Слайд 10Найдите абсциссу середины отрезка, соединяющего точки A(6; 8) и B(-2; 2).
Найдите ординату середины
отрезка, соединяющего точки A(6, 8) и B(-2, 2).