- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре Вероятность 11 класс
Содержание
- 1. Презентация по алгебре Вероятность 11 класс
- 2. Модуль 1. Простые задачиЗадача 1. В урне
- 3. Задачи о выборе объектов из набора Задача
- 4. Проверь себяЗадача 4. Научная конференция проводится в
- 5. Задачи о подбрасывании монетыЗадача 9. В случайном
- 6. Задачи о подбрасывании монеты Задача 10.
- 7. Задачи о подбрасывании кубикаЗадача 11. Игральный кубик
- 8. Задачи о подбрасывании кубикаЗадача 12. В случайном
- 9. Проверь себяЗадача 13. Одновременно бросают три игральные
- 10. Модуль2.Задачи средней трудностиПри решении задач этого модуля
- 11. Модуль2.Задачи средней трудностиОпределение. Два события А и
- 12. Задачи об объединении несовместных событийЗадача 19. На
- 13. Задачи об объединении несовместных событийЗадача 20. Из
- 14. Задачи о пересечении независимых событийЗадача 22. Если
- 15. Задачи о пересечении независимых событийЗадача 23. В
- 16. Назад
- 17. Проверь себяЗадача 25. В классе 21 шестиклассник,
- 18. Слайд 18
- 19. Модуль 3. Трудные задачи
- 20. Задачи о зависимых событияхКовбой Джон попадает в
- 21. Задачи о зависимых событияхВ торговом центре два
- 22. Задачи о зависимых событияхДве фабрики выпускают одинаковые
- 23. Решение: Для того, чтобы поступить хоть куда-нибудь,
- 24. Проверь себя Вариант 1 1)На чемпионате по прыжкам
- 25. Проверь себя1)На чемпионате по прыжкам в воду
- 26. Использованная литератураАлгебра и начала математического анализа.11 класс/
- 27. Назад
- 28. Задачи о подбрасывании монеты Назад
- 29. Задачи о подбрасывании кубика Назад
- 30. Задачи об объединении несовместных событийНазад
- 31. Проверь себяЗадача 4. 0,3Задача 5. 0,24Задача 6. 0,4 Задача 7. 0,992 Задача 8. 0 99Назад
- 32. Проверь себяЗадача 13. 0,03Задача 14. 0,83Задача 15. 0,07 Задача 16. 0,5Задача 17. 0,125Задача 18. 0,0625Назад
Слайд 1Модуль 1. Простые задачи
В этом модуле рассматриваются задачи, для решения которых
Слайд 2Модуль 1. Простые задачи
Задача 1. В урне 14 красных, 9 желтых
Слайд 3Задачи о выборе объектов из набора
Задача 2. В чемпионате по
Задача 3. Антон, Боря , Вова и Гриша бросили жребий – кому начинать игру. Найдите вероятность того, что начинать игру будет Вова.
Задача 4. Какова вероятность того, что случайно выбранное натуральное число от 4 до 23 делится на 3?
Решение
Слайд 4Проверь себя
Задача 4. Научная конференция проводится в 3 дня. Всего запланировано
Задача 5. В сборнике билетов по химии всего 25 билетов, в 6 из них встречается вопрос по углеводородам. Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику достанется вопрос по углеводородам.
Задача 6. Перед началом первого тура чемпионата по шашкам участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 36 шашистов, среди которых 15 участников из России, в том числе Евгений Коротов. Найдите вероятность того, что в первом туре Евгений Коротов будет играть с каким-либо шашистом из России?
Задача 7. В среднем из 500 садовых насосов, поступивших в продажу, 4 подтекают. Найдите вероятность того, что один случайно выбранный для контроля насос не подтекает.
Задача 8. Фабрика выпускает сумки. В среднем на 80 качественных сумок приходится одна сумка со скрытыми дефектами. Найдите вероятность того, что купленная сумка окажется качественной. Результат округлите до сотых
Ответы
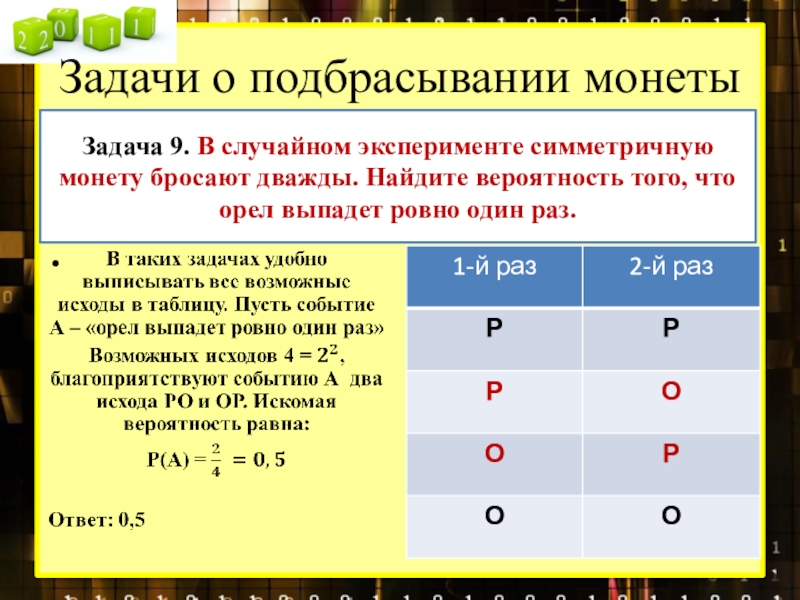
Слайд 5Задачи о подбрасывании монеты
Задача 9. В случайном эксперименте симметричную монету бросают
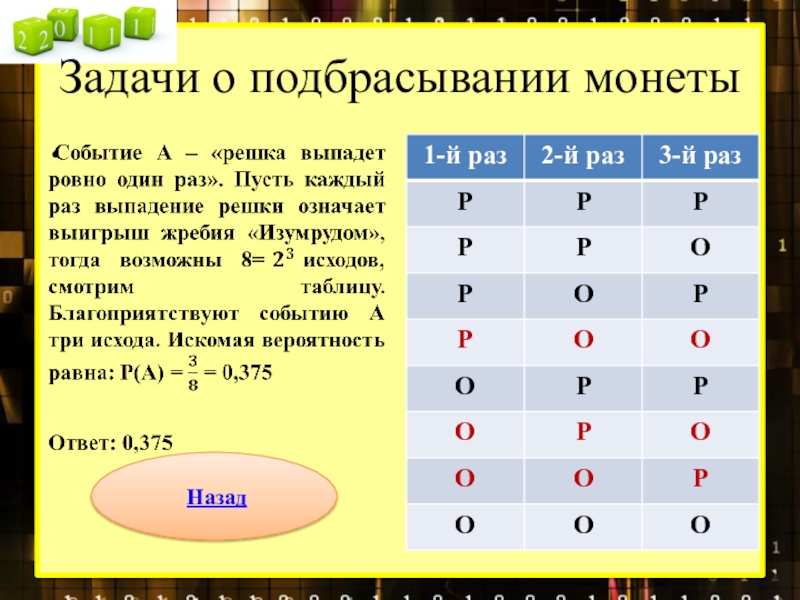
Слайд 6Задачи о подбрасывании монеты
Задача 10. Перед началом футбольного матча
Решение
Слайд 7Задачи о подбрасывании кубика
Задача 11. Игральный кубик бросают дважды. Найти вероятность
Слайд 8Задачи о подбрасывании кубика
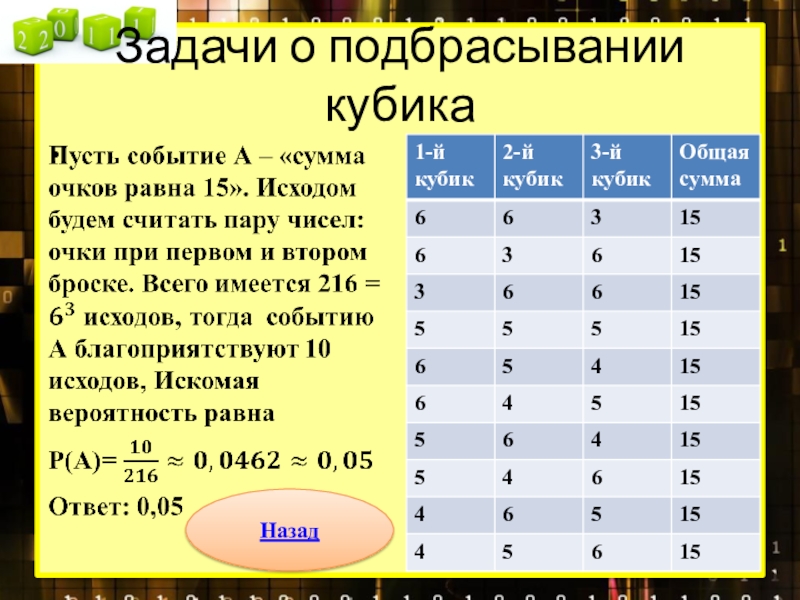
Задача 12. В случайном эксперименте бросают три игральные
Решение
Слайд 9Проверь себя
Задача 13. Одновременно бросают три игральные кости. Найти вероятность того,
Задача 14. Определите вероятность того, что при двух бросаниях кубика выпадет разное количество очков. Результат округлить до сотых.
Задача 15. В случайном эксперименте бросают три игральные кости. Найдите вероятность того, что в сумме выпадет 7 очков, Результат округлите до сотых.
Задача 16. Дважды бросают симметричную монету. Найдем вероятность того, что оба раза выпала одна сторона.
Задача 17. В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что орел не выпадет ни разу.
Задача 18. В случайном эксперименте симметричную монету бросают четырежды. Найдите вероятность того, что орел не выпадет ни разу.
Ответы
Слайд 10Модуль2.Задачи средней трудности
При решении задач этого модуля необходимы формулы вероятности для
К этому модулю относятся задачи , связанные с частотой и процентами.
Определение. Два события А и В называются несовместными, если они не могут происходить одновременно в одном и том же испытании.
Пример. Событие А – «при бросании кубика выпало число 3 » и событие В – « выпало четное число» несовместны.
Событие С – « выпало число больше 3-х» и событие Д – «выпало четное число» являются совместными событиями.
Теорема. Вероятность суммы двух несовместных событий A и B (появление хотя бы одного события) равна сумме вероятностей этих событий:
P(A+B)=P(A) +P(B)
Слайд 11Модуль2.Задачи средней трудности
Определение. Два события А и В называются независимыми, если
Пример. Производится бросание двух костей. Событие А- «при первом подбрасывании выпало нечетное число очков» и событие В – «при втором подбрасывании выпало нечетное число очков» являются независимыми.
Пример. Пусть в урне два черных и два белых шара. Событие А – «первый извлеченный шар белый» и событие В – «второй извлеченный шар черный» являются зависимыми.
Теорема. Вероятность произведения (совместного появления) двух независимых событий равна произведению вероятностей этих событий: P(AB) = P(A) · P(B).
,
на второй кости выпало нечетное число очков ,
Слайд 12Задачи об объединении несовместных событий
Задача 19. На экзамене по геометрии школьнику
Решение: пусть событие А означает, что школьнику достался вопрос по теме «Ромб», событие В – вопрос по теме «Тригонометрия». По условию Р(А)=0,1, Р(В)=0,35, события А и В несовместны. Искомая вероятность равна р(А+В) = 0,1+0,35 = 0,45
Ответ: 0,45
Слайд 13Задачи об объединении несовместных событий
Задача 20. Из районного центра в деревню
Решение
Задача 21. Вероятность того, что новая кофемолка прослужит больше года, равна 0,93. Вероятность того, что она прослужит больше двух лет, равна 0,81. Найдите вероятность того, что кофемолка прослужит меньше двух лет, но больше года.
Слайд 14Задачи о пересечении независимых событий
Задача 22. Если гроссмейстер А играет белыми,
Слайд 15Задачи о пересечении независимых событий
Задача 23. В магазине три продавца. Каждый
Задача 24. Биатлонист 5 раз стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,6. Найдите вероятность того, что биатлонист первые 2 раза попал в мишени, а последние три промахнулся. Результат округлите до сотых.
Решение
Слайд 17Проверь себя
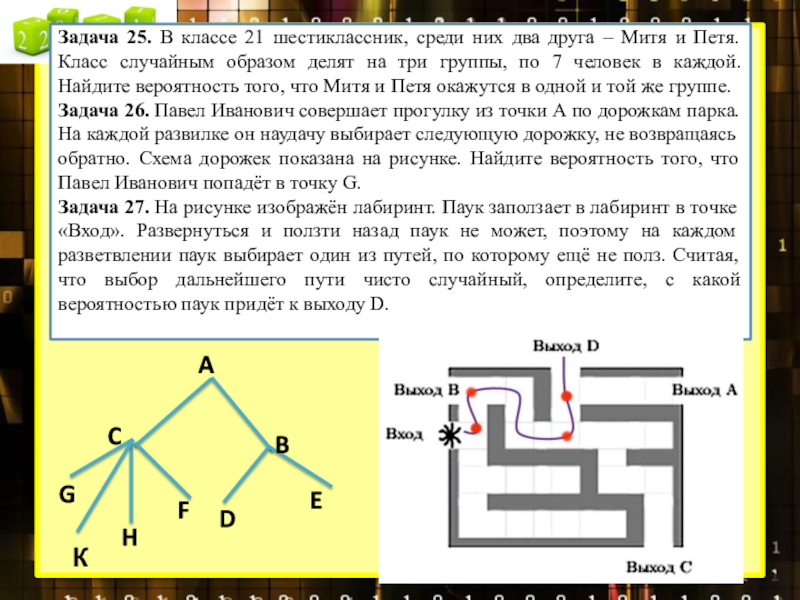
Задача 25. В классе 21 шестиклассник, среди них два друга
Задача 26. Павел Иванович совершает прогулку из точки А по дорожкам парка. На каждой развилке он наудачу выбирает следующую дорожку, не возвращаясь обратно. Схема дорожек показана на рисунке. Найдите вероятность того, что Павел Иванович попадёт в точку G.
Задача 27. На рисунке изображён лабиринт. Паук заползает в лабиринт в точке «Вход». Развернуться и ползти назад паук не может, поэтому на каждом разветвлении паук выбирает один из путей, по которому ещё не полз. Считая, что выбор дальнейшего пути чисто случайный, определите, с какой вероятностью паук придёт к выходу D.
Слайд 20Задачи о зависимых событиях
Ковбой Джон попадает в муху на стене с
Событие А – «Ковбой Джон схватит пристрелянный пистолет и попадет из него», событие В – «Ковбой Джон схватит непристрелянный пистолет и попадет из него».
По формуле условной вероятности, Р(А)=0,4 0,9=0,36, Р(В)=0,6 0,2=0,12. Эти события несовместны, вероятность их суммы равна сумме вероятностей: 0.36+0,12=0,48. Событие, состоящее в том, что Джон промахнется, противоположное. Искомая вероятность равна: 1-0,48=0,52
Ответ: 0,52
Слайд 21Задачи о зависимых событиях
В торговом центре два одинаковых автомата продают кофе.
Рассмотрим события
А = «кофе закончится в первом автомате»,
В = «кофе закончится во втором автомате».
Тогда A·B = «кофе закончится в обоих автоматах»,
A + B = «кофе закончится хотя бы в одном автомате».
По условию P(A) = P(B) = 0,2; P(A·B) = 0,16.
События A и B совместные, вероятность суммы двух совместных событий равна сумме вероятностей этих событий, уменьшенной на вероятность их произведения:
P(A + B) = P(A) + P(B) − P(A·B) = 0,2 + 0,2 − 0,16 = 0,24.
Следовательно, вероятность противоположного события, состоящего в том, что кофе останется в обоих автоматах, равна 1 − 0,24 = 0,76.
Ответ: 0,76.
Слайд 22Задачи о зависимых событиях
Две фабрики выпускают одинаковые стекла для автомобильных фар.
Ответ: 0,204
Чтобы поступить в институт на специальность «Лингвистика», абитуриент должен набрать на ЕГЭ не менее 70 баллов по каждому из трёх предметов – математика, русский язык и иностранный язык. Чтобы поступить на на специальность «Коммерция», нужно набрать не менее 70 баллов по каждому из трёх предметов – математика, русский язык и обществознание.
Вероятность того, что абитуриент З. получит не менее 70 баллов по математике, равна 0,6, по русскому языку – 0,8, по иностранному языку – 0,7 и по обществознанию – 0,5.
Найдите вероятность того, что З. сможет поступить хотя бы на одну из двух упомянутых специальностей.
Решение
Слайд 23Решение:
Для того, чтобы поступить хоть куда-нибудь, З. нужно сдать и
Р(С + D) = P(C) + P(D) – P(C · D),
для вероятности поступления имеем:
P(AB(C + D)) = P(A) · P(B) · P(C + D) = P(A) · P(B) · (P(C) + P(D) – P(C) · P(D)) = = 0,6 · 0,8 · (0,7 + 0,5 – 0,7 · 0,5) = 0,408.
Ответ: 0,408.
Назад
Слайд 24Проверь себя
Вариант 1
1)На чемпионате по прыжкам в воду выступают 20
2)В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 2 очка. Результат округлите до сотых.
3)На экзамене по геометрии школьнику достаётся один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос на тему «Тригонометрия», равна 0,35. Вероятность того, что это вопрос на тему «Вписанная окружность», равна 0,25. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.
4)В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,3. Вероятность того, что кофе закончится в обоих автоматах, равна 0,14. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.
5)В кармане у Пети было 2 монеты по 5 рублей и 4 монеты по 10 рублей. Петя, не глядя, переложил какие-то 3 монеты в другой карман. Найдите вероятность того, что пятирублевые монеты лежат теперь в разных карманах.
Слайд 25Проверь себя
1)На чемпионате по прыжкам в воду выступают 20 спортсменов, среди
2)В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 2 очка. Результат округлите до сотых.
3)На экзамене по геометрии школьнику достаётся один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос на тему «Тригонометрия», равна 0,35. Вероятность того, что это вопрос на тему «Вписанная окружность», равна 0,25. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.
4)В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,3. Вероятность того, что кофе закончится в обоих автоматах, равна 0,14. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.
5)В кармане у Пети было 2 монеты по 5 рублей и 4 монеты по 10 рублей. Петя, не глядя, переложил какие-то 3 монеты в другой карман. Найдите вероятность того, что пятирублевые монеты лежат теперь в разных карманах.
Ответы
1.0,5
2. 0,06
3. 0,6
3. 0,6
5. 0,6
Слайд 26Использованная литература
Алгебра и начала математического анализа.11 класс/ Ю.М.Колягин, М.В.Ткачева, Н.Е.Федорова, М.И.Шабунин.
2011
ЕГЭ-2016: Математика: самое полное издание типовых вариантов заданий/ авт.-сост. И.В.Ященко, И.Р. Высоцкий; под ред. А.Л.Семёнова, И.В.Ященко.- Москва: АСТ: Астрель, 2014.
http://alexlarin.net/ege/2014/b102014.html
http://math.reshuege.ru/test?a=catlistwstat
Слайд 32Проверь себя
Задача 13. 0,03
Задача 14. 0,83
Задача 15. 0,07
Задача 16.
Задача 17. 0,125
Задача 18. 0,0625
Назад