- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре в 8 классе на тему ЗАДАЧА, ПРИВОДЯЩАЯ К ПОНЯТИЮ СИСТЕМА УРАВНЕНИЙ (по учебнику Дорофеева Г.В., Суворовой С.Б. и др.)
Содержание
- 1. Презентация по алгебре в 8 классе на тему ЗАДАЧА, ПРИВОДЯЩАЯ К ПОНЯТИЮ СИСТЕМА УРАВНЕНИЙ (по учебнику Дорофеева Г.В., Суворовой С.Б. и др.)
- 2. Для каждой прямой назовите ее угловой
- 3. ДалееОбъяснение нового материала.б) 2x – 3y =
- 4. ДалееОбъяснение нового материала.В тех случаях, когда нужно
- 5. ДалееОбъяснение нового материала.1) Любое уравнение системы можно
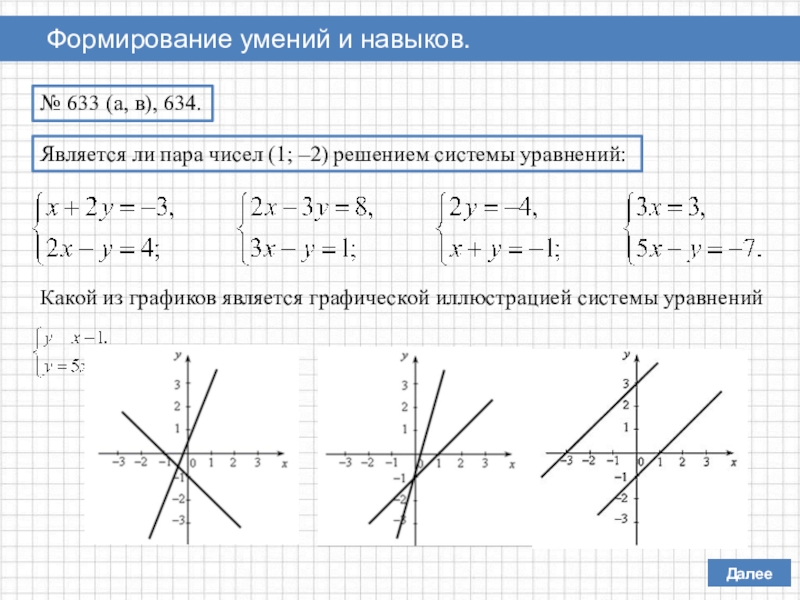
- 6. Далее Формирование умений и навыков.№ 633 (а,
- 7. На рисунке изображены две прямые. Какая из
- 8. Итоги урокаДомашнее задание: № 633 (б,
Слайд 1Алгебра-8
Далее
ЗАДАЧА, ПРИВОДЯЩАЯ К ПОНЯТИЮ
«СИСТЕМА УРАВНЕНИЙ»
Урок 69
Тимаев А.В., ОК-Г "Эврика"
Слайд 2 Для каждой прямой назовите ее угловой коэффициент и ординату точки,
Далее
Устная работа
Есть ли среди данных прямых параллельные?
Слайд 3Далее
Объяснение нового материала.
б) 2x – 3y = 3 и 4x +
Найдите координаты точки пересечения прямых:
а) x – y = 1 и 2x + y = 4;
Точка М принадлежит прямой 2x – 3y = 3. Что это означает?
Точка М принадлежит прямой 4x + 3y = 18. Что это означает?
Что можно сказать о координатах точки М ввиду того, что она принадлежит одновременно двум прямым?
К чему свелась задача о нахождении точки пересечения двух прямых?
Чтобы найти координаты точки пересечения двух прямых, нужно найти общее решение уравнений, задающих эти прямые.
Вывод.
Слайд 4Далее
Объяснение нового материала.
В тех случаях, когда нужно найти общее решение двух
«Решение системы уравнений» – это пара чисел, которая является решением каждого из уравнений, входящих в систему.
Слайд 5Далее
Объяснение нового материала.
1) Любое уравнение системы можно заменить уравнением, полученным путем
4) Получить противоположные или равные коэффициенты при какой-либо переменной можно путем умножения обеих частей уравнения системы на одно и то же, отличное от нуля, число.
3) Складывать (вычитать) нужно те уравнения, в которых коэффициенты при каких-либо переменных являются противоположными (равными) числами.
2) Целью такого преобразования является исключение одной из двух переменных.
Слайд 6Далее
Формирование умений и навыков.
№ 633 (а, в), 634.
Является ли пара
Какой из графиков является графической иллюстрацией системы уравнений
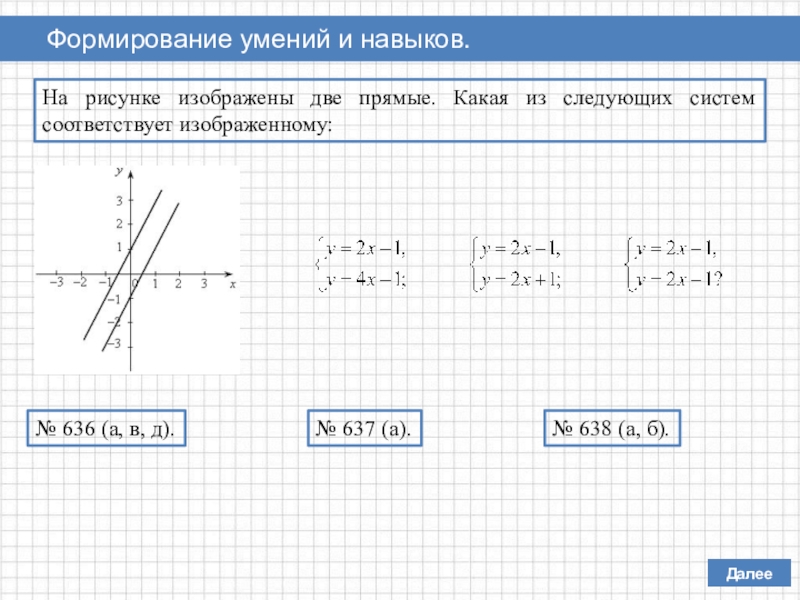
Слайд 7На рисунке изображены две прямые. Какая из следующих систем соответствует изображенному:
Далее
№ 636 (а, в, д).
№ 637 (а).
№ 638 (а, б).
Слайд 8Итоги урока
Домашнее задание: № 633 (б, г), 635, 636 (б,
В чем заключается способ сложения при решении системы уравнений?
Как алгебраически найти координаты точки пересечения двух прямых?
Что такое система уравнений?
Что называется решением системы уравнений?
Как выяснить, является ли пара чисел решением системы уравнений?
Каким способом можно решить систему уравнений?
Тимаев А.В., ОК-Г "Эврика"