- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре в 7 классе на тему Линейная функция и её график
Содержание
- 1. Презентация по алгебре в 7 классе на тему Линейная функция и её график
- 2. ЦЕЛЬ: ФОРМИРОВАНИЕ ПОНЯТИЯ «ЛИНЕЙНАЯ ФУНКЦИЯ», НАВЫКА ПОСТРОЕНИЯ
- 3. РАЗГАДАВ СЛОВА ПО ГОРИЗОНТАЛИ, ВЫ УЗНАЕТЕ КЛЮЧЕВОЕ
- 4. 1. ТОЧНЫЙ НАБОР ИНСТРУКЦИЙ, ОПИСЫВАЮЩИХ ПОРЯДОК ДЕЙСТВИЙ
- 5. ТУРИСТ ПРОЕХАЛ
- 6. III. ИЗУЧЕНИЕ НОВОЙ ТЕМЫ. УРАВНЕНИЕ ВИДА Y=K
- 7. 2112
- 8. Слайд 8
- 9. АЛГОРИТМ ПОСТРОЕНИЯ ГРАФИКА ЛИНЕЙНОЙ ФУНКЦИИ1)
- 10. РАССМОТРИМ ПРИМЕНЕНИЕ АЛГОРИТМА ДЛЯ ПОСТРОЕНИЯ ГРАФИКА ЛИНЕЙНОЙ
- 11. ЕСЛИ ЛИНЕЙНУЮ ФУНКЦИЮ Y=K X+ M
- 12. ПРИМЕР 2 ПОСТРОИТЬ ГРАФИК ЛИНЕЙНОЙ ФУНКЦИИ
- 13. ВЫПОЛНЯЕМ ПОСТРОЕНИЕ ГРАФИКА ФУНКЦИИ Y = -2X + 1, [ -3; 2]
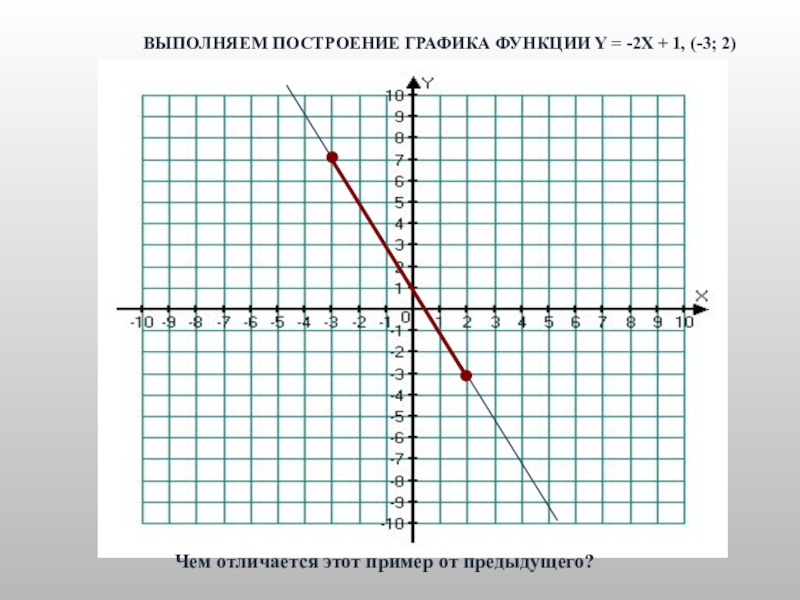
- 14. ВЫПОЛНЯЕМ ПОСТРОЕНИЕ ГРАФИКА ФУНКЦИИ Y = -2X + 1, (-3; 2)Чем отличается этот пример от предыдущего?
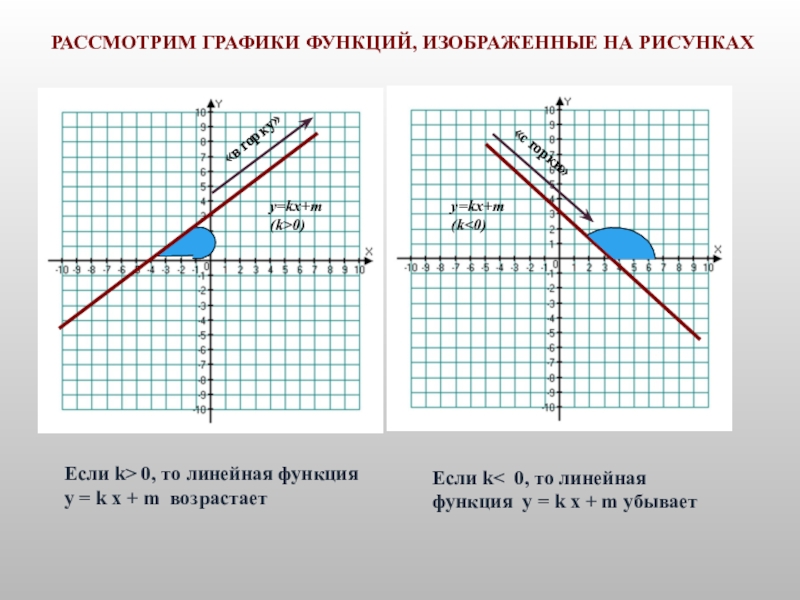
- 15. РАССМОТРИМ ГРАФИКИ ФУНКЦИЙ, ИЗОБРАЖЕННЫЕ НА РИСУНКАХ
- 16. ВЫБЕРИТЕ, КАКАЯ ФУНКЦИЯ ЯВЛЯЕТСЯ ЛИНЕЙНОЙ ФУНКЦИЕЙ
- 17. ЛИНЕЙНАЯ ФУНКЦИЯ ЗАДАНА ФОРМУЛОЙ
- 18. ПРОВЕРКА РЕШЕНИЯ ЕСЛИ X = 23, ТО
- 19. НАЙДИТЕ ЗНАЧЕНИЕ АРГУМЕНТА, ПРИ КОТОРОМ ЛИНЕЙНАЯ
- 20. НЕ ВЫПОЛНЯЯ ПОСТРОЕНИЯ ОТВЕТЬТЕ НА ВОПРОС: ГРАФИКУ КАКОЙ ФУНКЦИИ ПРИНАДЛЕЖИТ А (1;0)?
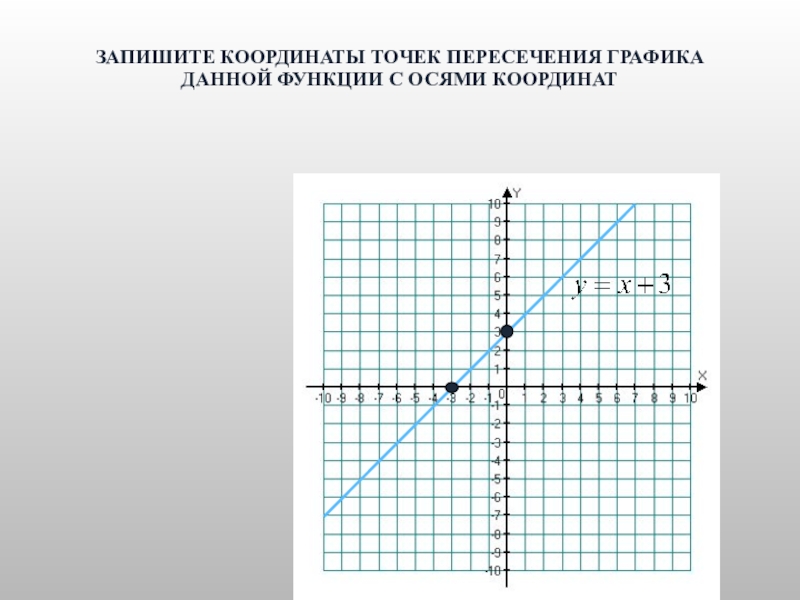
- 21. ЗАПИШИТЕ КООРДИНАТЫ ТОЧЕК ПЕРЕСЕЧЕНИЯ ГРАФИКА ДАННОЙ ФУНКЦИИ С ОСЯМИ КООРДИНАТ
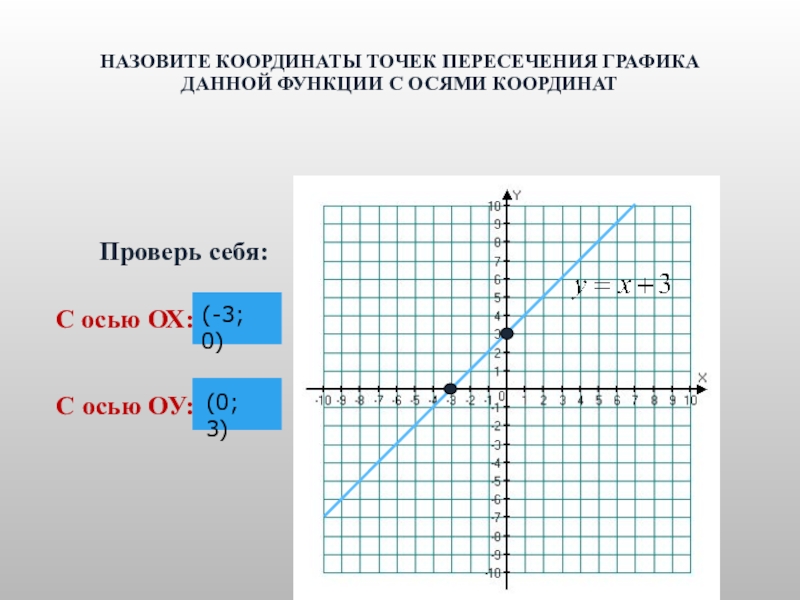
- 22. НАЗОВИТЕ КООРДИНАТЫ ТОЧЕК ПЕРЕСЕЧЕНИЯ ГРАФИКА ДАННОЙ ФУНКЦИИ
- 23. ДОМАШНЕЕ ЗАДАНИЕ:
- 24. VII. РЕФЛЕКСИЯЯ РАБОТАЛ(А) ОТЛИЧНО, В ПОЛНУЮ СИЛУ
Слайд 2ЦЕЛЬ: ФОРМИРОВАНИЕ ПОНЯТИЯ «ЛИНЕЙНАЯ ФУНКЦИЯ», НАВЫКА ПОСТРОЕНИЯ ЕЁ ГРАФИКА ПО АЛГОРИТМУ
ЗАДАЧИ:
ОБРАЗОВАТЕЛЬНЫЕ:
-
- ВВЕСТИ И ИЗУЧИТЬ АЛГОРИТМ ПОСТРОЕНИЯ ГРАФИКА ЛИНЕЙНОЙ ФУНКЦИИ,
- ОТРАБОТАТЬ НАВЫК РАСПОЗНАВАНИЯ ЛИНЕЙНОЙ ФУНКЦИИ ПО ЗАДАННОЙ ФОРМУЛЕ, ГРАФИКУ, СЛОВЕСНОМУ ОПИСАНИЮ.
РАЗВИВАЮЩИЕ:
- РАЗВИВАТЬ ЗРИТЕЛЬНУЮ ПАМЯТЬ, МАТЕМАТИЧЕСКИ ГРАМОТНУЮ РЕЧЬ, АККУРАТНОСТЬ, ТОЧНОСТЬ В ПОСТРОЕНИИ, УМЕНИЕ АНАЛИЗИРОВАТЬ.
ВОСПИТАТЕЛЬНЫЕ:
- ВОСПИТЫВАТЬ ОТВЕТСТВЕННОЕ ОТНОШЕНИЕ К УЧЕБНОМУ ТРУДУ, АККУРАТНОСТЬ, ДИСЦИПЛИНИРОВАННОСТЬ, УСИДЧИВОСТЬ.
- ФОРМИРОВАТЬ НАВЫКИ САМОКОНТРОЛЯ И ВЗАИМОКОНТРОЛЯ
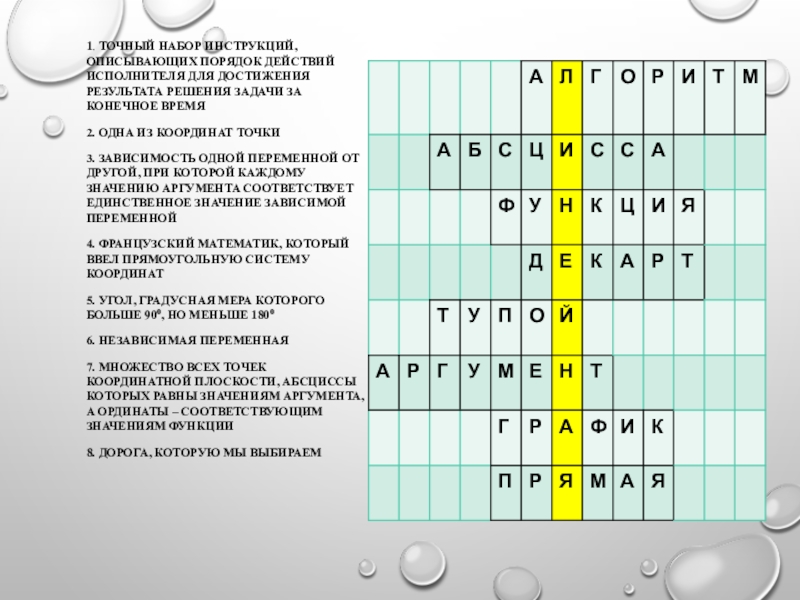
Слайд 3РАЗГАДАВ СЛОВА ПО ГОРИЗОНТАЛИ, ВЫ УЗНАЕТЕ КЛЮЧЕВОЕ СЛОВО
1. ТОЧНЫЙ НАБОР ИНСТРУКЦИЙ,
2. ОДНА ИЗ КООРДИНАТ ТОЧКИ
3. ЗАВИСИМОСТЬ ОДНОЙ ПЕРЕМЕННОЙ ОТ ДРУГОЙ, ПРИ КОТОРОЙ КАЖДОМУ ЗНАЧЕНИЮ АРГУМЕНТА СООТВЕТСТВУЕТ ЕДИНСТВЕННОЕ ЗНАЧЕНИЕ ЗАВИСИМОЙ ПЕРЕМЕННОЙ
4. ФРАНЦУЗСКИЙ МАТЕМАТИК, КОТОРЫЙ ВВЕЛ ПРЯМОУГОЛЬНУЮ СИСТЕМУ КООРДИНАТ
5. УГОЛ, ГРАДУСНАЯ МЕРА КОТОРОГО БОЛЬШЕ 900, НО МЕНЬШЕ 1800
6. НЕЗАВИСИМАЯ ПЕРЕМЕННАЯ
7. МНОЖЕСТВО ВСЕХ ТОЧЕК КООРДИНАТНОЙ ПЛОСКОСТИ, АБСЦИССЫ КОТОРЫХ РАВНЫ ЗНАЧЕНИЯМ АРГУМЕНТА, А ОРДИНАТЫ – СООТВЕТСТВУЮЩИМ ЗНАЧЕНИЯМ ФУНКЦИИ
8. ДОРОГА, КОТОРУЮ МЫ ВЫБИРАЕМ
Слайд 41. ТОЧНЫЙ НАБОР ИНСТРУКЦИЙ, ОПИСЫВАЮЩИХ ПОРЯДОК ДЕЙСТВИЙ ИСПОЛНИТЕЛЯ ДЛЯ ДОСТИЖЕНИЯ РЕЗУЛЬТАТА
2. ОДНА ИЗ КООРДИНАТ ТОЧКИ
3. ЗАВИСИМОСТЬ ОДНОЙ ПЕРЕМЕННОЙ ОТ ДРУГОЙ, ПРИ КОТОРОЙ КАЖДОМУ ЗНАЧЕНИЮ АРГУМЕНТА СООТВЕТСТВУЕТ ЕДИНСТВЕННОЕ ЗНАЧЕНИЕ ЗАВИСИМОЙ ПЕРЕМЕННОЙ
4. ФРАНЦУЗСКИЙ МАТЕМАТИК, КОТОРЫЙ ВВЕЛ ПРЯМОУГОЛЬНУЮ СИСТЕМУ КООРДИНАТ
5. УГОЛ, ГРАДУСНАЯ МЕРА КОТОРОГО БОЛЬШЕ 900, НО МЕНЬШЕ 1800
6. НЕЗАВИСИМАЯ ПЕРЕМЕННАЯ
7. МНОЖЕСТВО ВСЕХ ТОЧЕК КООРДИНАТНОЙ ПЛОСКОСТИ, АБСЦИССЫ КОТОРЫХ РАВНЫ ЗНАЧЕНИЯМ АРГУМЕНТА, А ОРДИНАТЫ – СООТВЕТСТВУЮЩИМ ЗНАЧЕНИЯМ ФУНКЦИИ
8. ДОРОГА, КОТОРУЮ МЫ ВЫБИРАЕМ
Слайд 5 ТУРИСТ ПРОЕХАЛ НА АВТОБУСЕ 15 КМ ОТ ПУНКТА А ДО ПУНКТА
МАТЕМАТИЧЕСКОЙ МОДЕЛЬЮ СИТУАЦИИ ЯВЛЯЕТСЯ ВЫРАЖЕНИЕ Y = 15 + 4X, ГДЕ X – ВРЕМЯ ХОДЬБЫ В ЧАСАХ, Y – РАССТОЯНИЕ ОТ А ( В КИЛОМЕТРАХ ). С ПОМОЩЬЮ ЭТОЙ МОДЕЛИ ОТВЕЧАЕМ НА ВОПРОС ЗАДАЧИ:
ЕСЛИ X = 2, ТО Y =15 + 4 ∙ 2 = 23
ЕСЛИ X = 4, ТО Y = 15 + 4 ∙ 4= 31
ЕСЛИ X = 6, ТО Y = 15 + 4 ∙ 6 = 39
МАТЕМАТИЧЕСКАЯ МОДЕЛЬ Y = 15 + 4X ЯВЛЯЕТСЯ ЛИНЕЙНОЙ ФУНКЦИЕЙ.
А
В
С
Слайд 6III. ИЗУЧЕНИЕ НОВОЙ ТЕМЫ. УРАВНЕНИЕ ВИДА Y=K X+ M , ГДЕ
ЧТОБЫ ПОСТРОИТЬ ГРАФИК ЛИНЕЙНОЙ ФУНКЦИИ НАДО , УКАЗАВ КОНКРЕТНОЕ ЗНАЧЕНИЕ X, ВЫЧИСЛИТЬ СООТВЕТСТВУЮЩЕЕ ЗНАЧЕНИЕ Y.
ОБЫЧНО ЭТИ РЕЗУЛЬТАТЫ ОФОРМЛЯЮТ В ВИДЕ ТАБЛИЦЫ.
ГОВОРЯТ, ЧТО X – НЕЗАВИСИМАЯ ПЕРЕМЕННАЯ (ИЛИ АРГУМЕНТ), Y – ЗАВИСИМАЯ ПЕРЕМЕННАЯ.
2
1
1
2
Слайд 9 АЛГОРИТМ ПОСТРОЕНИЯ ГРАФИКА ЛИНЕЙНОЙ ФУНКЦИИ
1) СОСТАВИТЬ ТАБЛИЦУ ДЛЯ ЛИНЕЙНОЙ
2) ПОСТРОИТЬ НА КООРДИНАТНОЙ ПЛОСКОСТИ XOY ТОЧКИ
3) ПРОВЕСТИ ЧЕРЕЗ НИХ ПРЯМУЮ – ГРАФИК ЛИНЕЙНОЙ ФУНКЦИИ
Теорема
Графиком линейной функции y = k x + m является прямая.
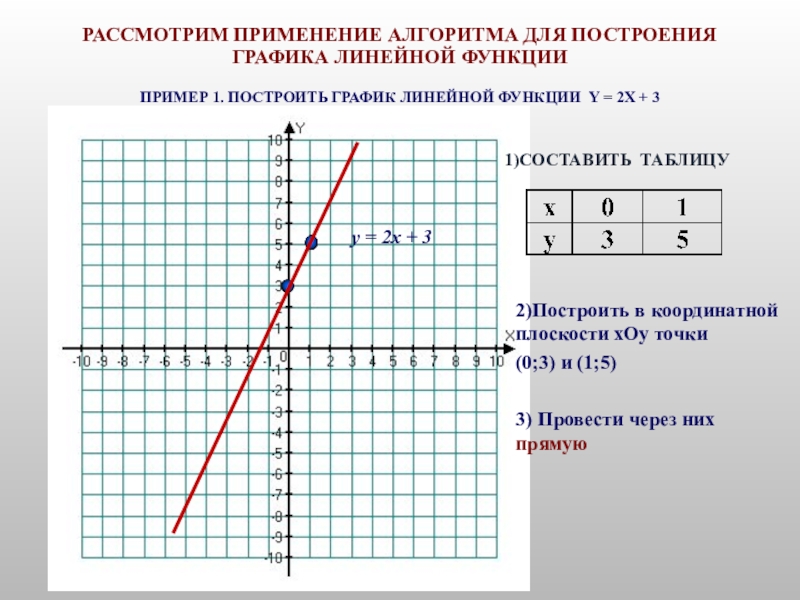
Слайд 10РАССМОТРИМ ПРИМЕНЕНИЕ АЛГОРИТМА ДЛЯ ПОСТРОЕНИЯ ГРАФИКА ЛИНЕЙНОЙ ФУНКЦИИ ПРИМЕР 1. ПОСТРОИТЬ ГРАФИК
1)СОСТАВИТЬ ТАБЛИЦУ
2)Построить в координатной плоскости xОy точки
(0;3) и (1;5)
3) Провести через них прямую
Слайд 11
ЕСЛИ ЛИНЕЙНУЮ ФУНКЦИЮ Y=K X+ M РАССМАТРИВАТЬ НЕ ПРИ ВСЕХ
В НАШЕЙ СИТУАЦИИ НЕЗАВИСИМАЯ ПЕРЕМЕННАЯ МОЖЕТ ПРИНЯТЬ ЛЮБОЕ НЕОТРИЦАТЕЛЬНОЕ ЗНАЧЕНИЕ , НО ПРАКТИЧЕСКИ ТУРИСТ НЕ МОЖЕТ ШАГАТЬ С ПОСТОЯННОЙ СКОРОСТЬЮ БЕЗ СНА И ОТДЫХА СКОЛЬКО УГОДНО ВРЕМЕНИ.
ЗНАЧИТ, НУЖНО БЫЛО СДЕЛАТЬ РАЗУМНЫЕ ОГРАНИЧЕНИЯ НА X, СКАЖЕМ, ТУРИСТ ИДЁТ НЕ БОЛЕЕ 6 Ч.
ТЕПЕРЬ ЗАПИШЕМ БОЛЕЕ ТОЧНУЮ МАТЕМАТИЧЕСКУЮ МОДЕЛЬ:
Y = 15 + 4X, X ∈ [ 0; 6]
Слайд 12 ПРИМЕР 2 ПОСТРОИТЬ ГРАФИК ЛИНЕЙНОЙ ФУНКЦИИ А) Y = -2X + 1,
1) СОСТАВИМ ТАБЛИЦУ ДЛЯ ЛИНЕЙНОЙ ФУНКЦИИ
Y = -2X + 1
2) ПОСТРОИМ НА КООРДИНАТНОЙ ПЛОСКОСТИ XOY
ТОЧКИ (-3;7) И (2;-3) И ПРОВЕДЁМ ЧЕРЕЗ НИХ
ПРЯМУЮ ЛИНИЮ. ЭТО ГРАФИК УРАВНЕНИЯ Y = -2X + 1. ДАЛЕЕ, ВЫДЕЛИМ ОТРЕЗОК, СОЕДИНЯЮЩИЙ ПОСТРОЕННЫЕ ТОЧКИ.
Слайд 14ВЫПОЛНЯЕМ ПОСТРОЕНИЕ ГРАФИКА ФУНКЦИИ Y = -2X + 1, (-3; 2)
Чем
Слайд 17
ЛИНЕЙНАЯ ФУНКЦИЯ ЗАДАНА ФОРМУЛОЙ
Y = -3X – 5.
НАЙДИТЕ ЕЁ ЗНАЧЕНИЕ
Слайд 18ПРОВЕРКА РЕШЕНИЯ
ЕСЛИ X = 23, ТО Y = -3* 23
ЕСЛИ X = -5, ТО Y = -3 * (-5) – 5= 15– 5 = 10
ЕСЛИ X = 0, ТО Y = -3* 0– 5= 0 – 5= -5
Слайд 19НАЙДИТЕ ЗНАЧЕНИЕ АРГУМЕНТА, ПРИ КОТОРОМ ЛИНЕЙНАЯ ФУНКЦИЯ Y = -2X +
ПРОВЕРКА РЕШЕНИЯ
ПРИ X = -9 ЗНАЧЕНИЕ ФУНКЦИИ РАВНО 20,4
20,4 = - 2x + 2,4
2x =2,4 – 20,4
2x = -18
x= -18:2
x = -9
Слайд 22
НАЗОВИТЕ КООРДИНАТЫ ТОЧЕК ПЕРЕСЕЧЕНИЯ ГРАФИКА ДАННОЙ ФУНКЦИИ С ОСЯМИ КООРДИНАТ
С осью
(-3; 0)
Проверь себя:
С осью ОУ:
(0; 3)
Слайд 24VII. РЕФЛЕКСИЯ
Я РАБОТАЛ(А) ОТЛИЧНО, В ПОЛНУЮ СИЛУ СВОИХ ВОЗМОЖНОСТЕЙ, ЧУВСТВОВАЛ(А) СЕБЯ
Я РАБОТАЛ(А) ХОРОШО, НО НЕ В ПОЛНУЮ СИЛУ, ИСПЫТЫВАЛ(А) ЧУВСТВО НЕУВЕРЕННОСТИ, БОЯЗНИ, ЧТО ОТВЕЧУ НЕПРАВИЛЬНО.
- У МЕНЯ НЕ БЫЛО ЖЕЛАНИЯ РАБОТАТЬ. СЕГОДНЯ НЕ МОЙ ДЕНЬ.










![Презентация по алгебре в 7 классе на тему Линейная функция и её график ВЫПОЛНЯЕМ ПОСТРОЕНИЕ ГРАФИКА ФУНКЦИИ Y = -2X + 1, [ -3; 2] ВЫПОЛНЯЕМ ПОСТРОЕНИЕ ГРАФИКА ФУНКЦИИ Y = -2X + 1, [ -3; 2]](/img/thumbs/10a5aa6997a18bacc3691513ab288cd0-800x.jpg)