- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре Свойства функций(9 класс)
Содержание
- 1. Презентация по алгебре Свойства функций(9 класс)
- 2. Свойства функции
- 3. Монотонность ВозрастающаяФункцию у = f(х) называют
- 4. Наибольшее и наименьшее значенияЧисло m называют наименьшим
- 5. НепрерывностьНепрерывность функции на промежутке Х означает, что
- 6. Свойства функцииЧЕТНОСТЬГоворят, что множество Х симметрично относительно
- 7. ВыпуклостьФункция выпукла вниз
- 8. ОграниченностьФункцию у = f(х) называют ограниченной снизу
- 9. Алгоритм описания свойств функцийОбласть определенияОбласть значенийЧетность МонотонностьНепрерывностьОграниченностьНаибольшее и наименьшее значенияНули функцииВыпуклостьСвойства функции
- 10. Опишите свойства функций:у= kx + m
- 11. Свойства функции y = kx +
- 12. Свойства функции у = kх2
- 13. Свойства функции
- 14. Функция D(f) =
- 15. Функция у =
- 16. Слайд 16
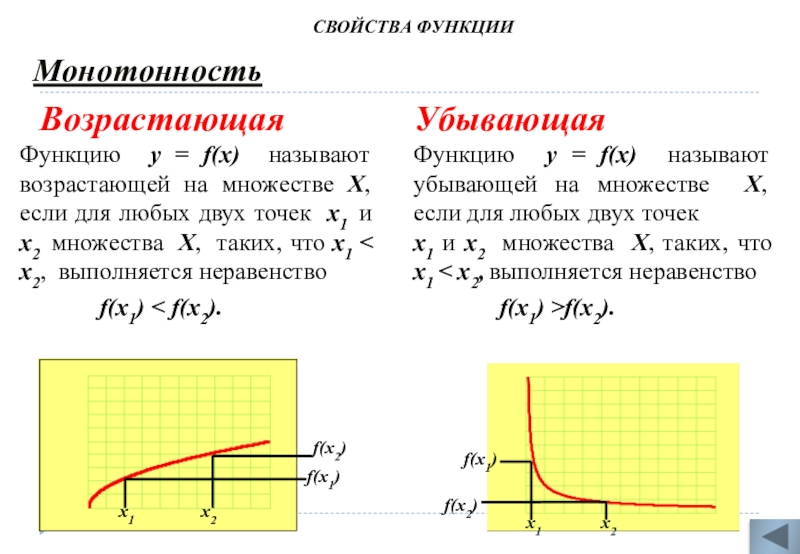
Слайд 3Монотонность
Возрастающая
Функцию у = f(х) называют возрастающей на
f(х1) < f(х2).
Убывающая
Функцию у = f(х) называют убывающей на множестве Х, если для любых двух точек
х1 и х2 множества Х, таких, что х1 < х2, выполняется неравенство
f(х1) >f(х2).
x1
x2
f(x1)
f(x2)
х1
x2
f(x2)
f(x1)
Свойства функции
Слайд 4Наибольшее и наименьшее значения
Число m называют наименьшим значением функции
у =
в Х существует такая точка х0, что f(х0) = m.
для всех х из Х выполняется неравенство
f(х) ≥ f(х0).
Число M называют наибольшим значением функции
у = f(х) на множестве Х, если:
в Х существует такая точка х0, что f(х0) = M.
для всех х из Х выполняется неравенство
f(х) ≤ f(х0).
Свойства функции
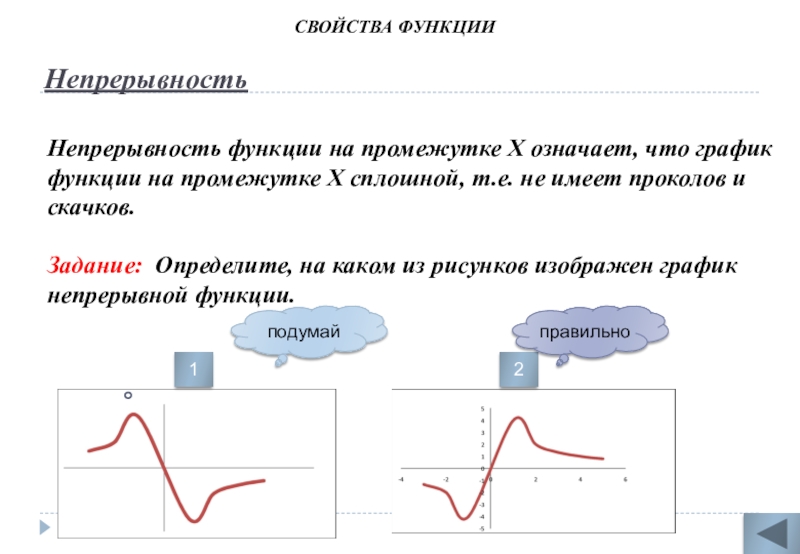
Слайд 5Непрерывность
Непрерывность функции на промежутке Х означает, что график функции на промежутке
Задание: Определите, на каком из рисунков изображен график непрерывной функции.
Свойства функции
1
2
подумай
правильно
Слайд 6Свойства функции
ЧЕТНОСТЬ
Говорят, что множество Х симметрично относительно начала
координат, если множество
Четная функция
Нечетная функция
Функция y = f(x) называется четной, если область ее определения есть множество, симметричное относительно начала координат, и если f (-x) = f (x) при любом х Х. Четная функция симметрична относительно оси ординат.
Функция y = f(x) называется четной, если область ее определения есть множество, симметричное относительно начала координат, и если f (-x) = f (x) при любом х Х. Нечетная функция симметрична относительно начала координат.
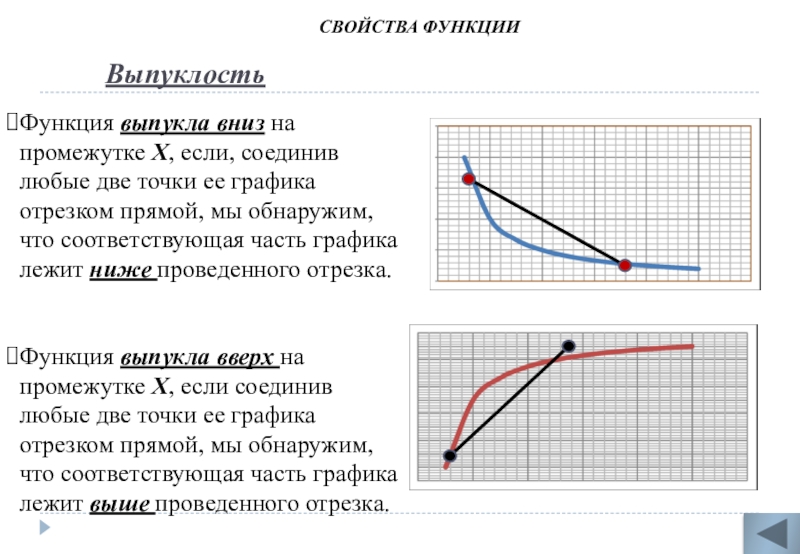
Слайд 7 Выпуклость
Функция выпукла вниз на промежутке Х, если,
Функция выпукла вверх на промежутке Х, если соединив любые две точки ее графика отрезком прямой, мы обнаружим, что соответствующая часть графика лежит выше проведенного отрезка.
Свойства функции
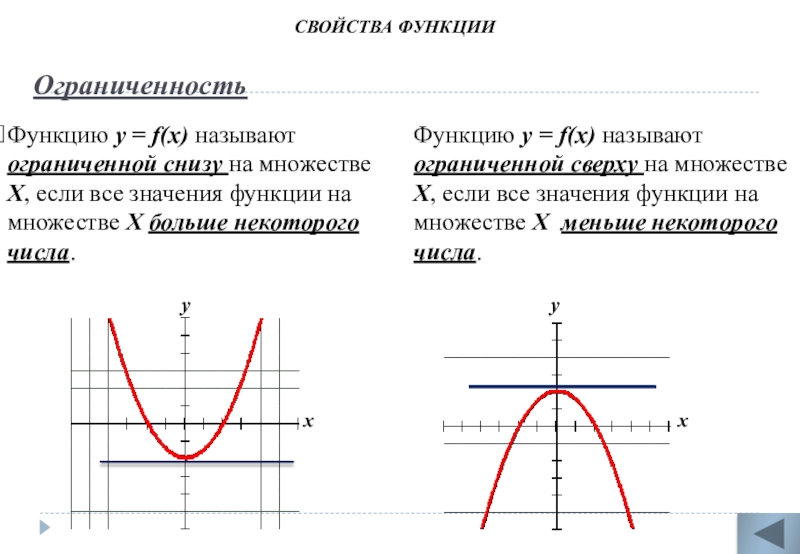
Слайд 8Ограниченность
Функцию у = f(х) называют ограниченной снизу на множестве Х, если
Функцию у = f(х) называют ограниченной сверху на множестве Х, если все значения функции на множестве Х меньше некоторого числа.
х
у
х
у
Свойства функции
Слайд 9Алгоритм описания свойств функций
Область определения
Область значений
Четность
Монотонность
Непрерывность
Ограниченность
Наибольшее и наименьшее значения
Нули функции
Выпуклость
Свойства
Слайд 10Опишите свойства функций:
у= kx + m
у = kx2 – квадратичная функция
у = k/x – обратная пропорциональность
у =
у = | х |
у = ах2 + bх + с – квадратичная функция
Свойства функции
Слайд 11Свойства функции y = kx + m (k ≠ 0)
E(f) = (-∞; +∞);
ни четная, ни нечетная;
возрастает при k > 0,
убывает при k < 0;
непрерывная
не ограничена ни снизу, ни сверху;
нет ни наибольшего, ни наименьшего значений;
y = 0, при
о выпуклости говорить не имеет смысла.
Свойства функции
k > 0
k < 0
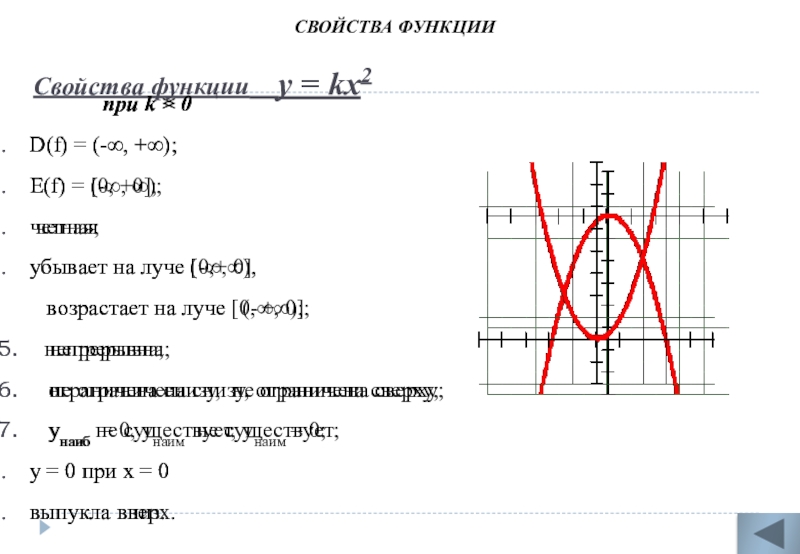
Слайд 12Свойства функции у = kх2
D(f) = (-∞, +∞);
E(f) = [0, +∞);
четная;
убывает на луче (-∞, 0],
возрастает на луче [0, +∞);
непрерывна;
ограничена снизу, не ограничена сверху;
унаиб не существует, унаим = 0;
y = 0 при х = 0
выпукла вниз.
при k < 0
D(f) = (-∞, +∞);
Е(f) = (-∞, 0];
четная
убывает на луче [0,+∞),
возрастает на луче (-∞, 0];
непрерывна;
не ограничена снизу, ограничена сверху;
унаиб = 0, унаим не существует;
y = 0 при х = 0
выпукла вверх.
Свойства функции
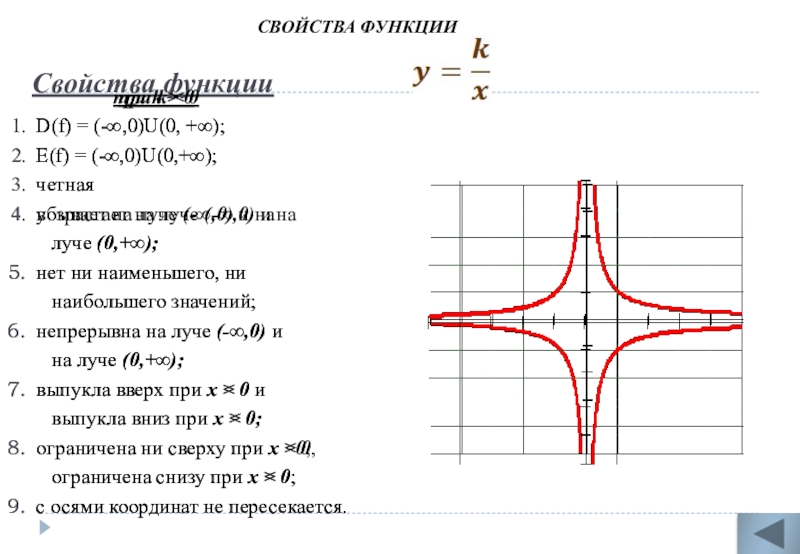
Слайд 13Свойства функции
D(f) = (-∞,0)U(0, +∞);
Е(f) = (-∞,0)U(0,+∞);
четная
убывает на луче (-∞,0) и на
луче (0,+∞);
нет ни наименьшего, ни
наибольшего значений;
непрерывна на луче (-∞,0) и
на луче (0,+∞);
выпукла вверх при х < 0 и
выпукла вниз при х > 0;
ограничена ни сверху при х < 0,
ограничена снизу при х > 0;
с осями координат не пересекается.
при k < 0
D(f) = (-∞,0)U(0, +∞);
Е(f) = (-∞,0)U(0,+∞);
четная
возрастает на луче (-∞,0) и на
луче (0,+∞);
нет ни наименьшего, ни
наибольшего значений;
непрерывна на луче (-∞,0) и
на луче (0,+∞);
выпукла вверх при х > 0 и
выпукла вниз при х < 0;
ограничена ни сверху при х >0,
ограничена снизу при х < 0;
с осями координат не пересекается.
Свойства функции
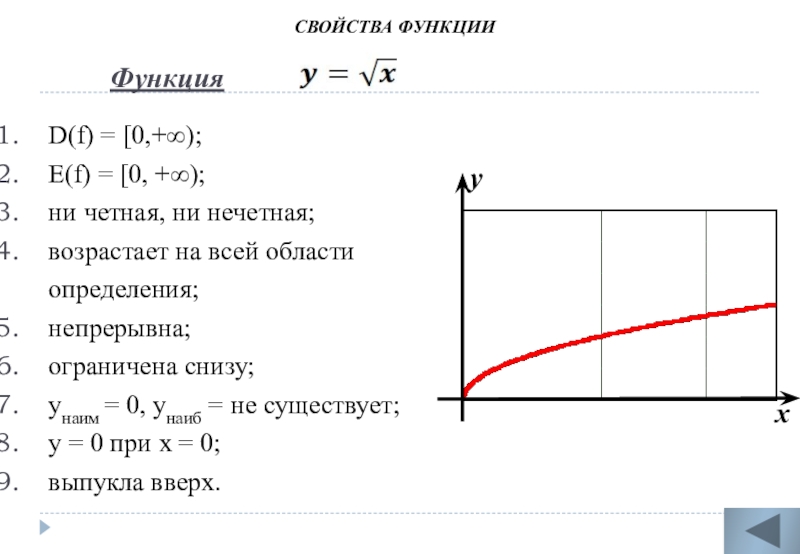
Слайд 14 Функция
D(f) = [0,+∞);
Е(f) = [0, +∞);
ни
возрастает на всей области определения;
непрерывна;
ограничена снизу;
унаим = 0, унаиб = не существует;
у = 0 при х = 0;
выпукла вверх.
Свойства функции
y
x
Слайд 15 Функция у = |х|
D(f) = (-∞,+∞);
Е(f) =
четная;
убывает на луче (-∞,0], возрастает на луче [0, +∞);
непрерывна;
ограничена снизу, не ограничена сверху;
унаим = 0, унаиб = не существует;
у = 0 при х = 0;
можно считать выпуклой вниз.
Свойства функции
Слайд 16 Функция у = ах2
при а > 0
D(f) = (-∞, +∞);
Е(f) = [у0 ; +∞)
убывает на луче ,
возрастает на луче ;
ограничена снизу;
унаим = у0, унаиб не существует;
непрерывна;
выпукла вниз;
Свойства функции
при а < 0
D(f) = (-∞, +∞);
Е(f) = (-∞; у0 ]
убывает на луче ,
возрастает на луче ;
ограничена сверху;
унаим не существует, унаиб = у0;
непрерывна;
выпукла вверх.






![Презентация по алгебре Свойства функций(9 класс) Функция у = |х|D(f) = (-∞,+∞);Е(f) = [0, +∞);четная;убывает Функция у = |х|D(f) = (-∞,+∞);Е(f) = [0, +∞);четная;убывает на луче (-∞,0], возрастает](/img/thumbs/ca14d6abc45343dd551c44f1561da40a-800x.jpg)