- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре Степенная функция (8 класс)
Содержание
- 1. Презентация по алгебре Степенная функция (8 класс)
- 2. Цели:ввести понятие квадратичной функции;научится строить график
- 3. Определение. Квадратичной функцией называется функция, которую
- 4. Из приведенных примеров укажите те функции, которые являются квадратичными. Для квадратичных функций назовите коэффициенты.
- 5. Функция у=ах2, ее график и свойства.
- 6. Построим графики функций и исследуем их свойства. 1)9410149
- 7. Построим графики функций и исследуем их
- 8. Построим графики функций и исследуем их
- 9. Построим графики функций и исследуем их
- 10. Построим графики функций и исследуем их
- 11. График функции у=kx2 может быть
- 12. Построим графики функций и исследуем их
- 13. График функции у=
- 14. Построим графики функций и исследуем их
- 15. Построим графики функций и исследуем их свойства. 4)-4,5-2-0,50-0,5-2-4,51. D(y): R2. у=0, если х=03. у
- 16. График функции у=ах2 симметричен графику
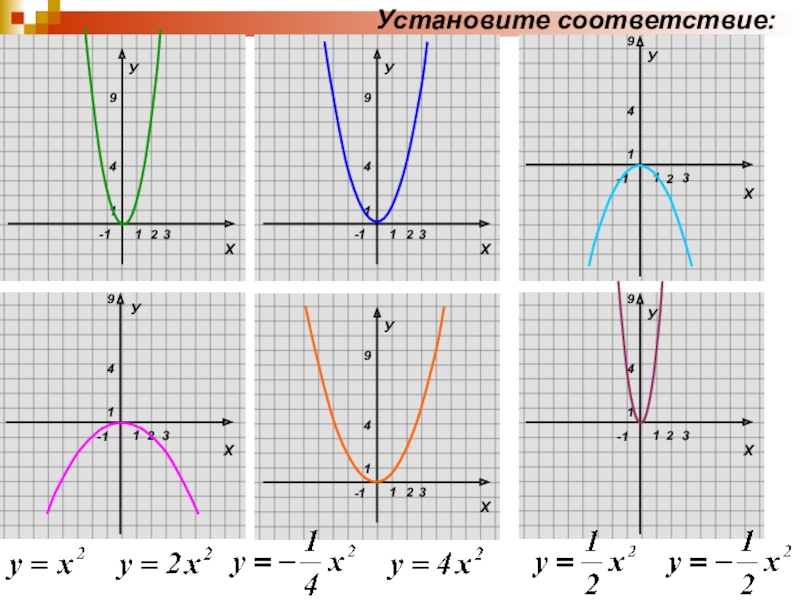
- 17. УУУУстановите соответствие:
Слайд 2 Цели:
ввести понятие квадратичной функции;
научится строить график функции у=ах2 и описывать
установить закономерность между графиком функции у=ах2 и значением коэффициента а.
Слайд 3Определение.
Квадратичной функцией называется функция, которую можно задать формулой вида
у=ах2+bx+c,
некоторые числа, причем а≠0.
Слайд 4
Из приведенных примеров укажите те функции,
которые являются квадратичными. Для квадратичных
функций назовите коэффициенты.
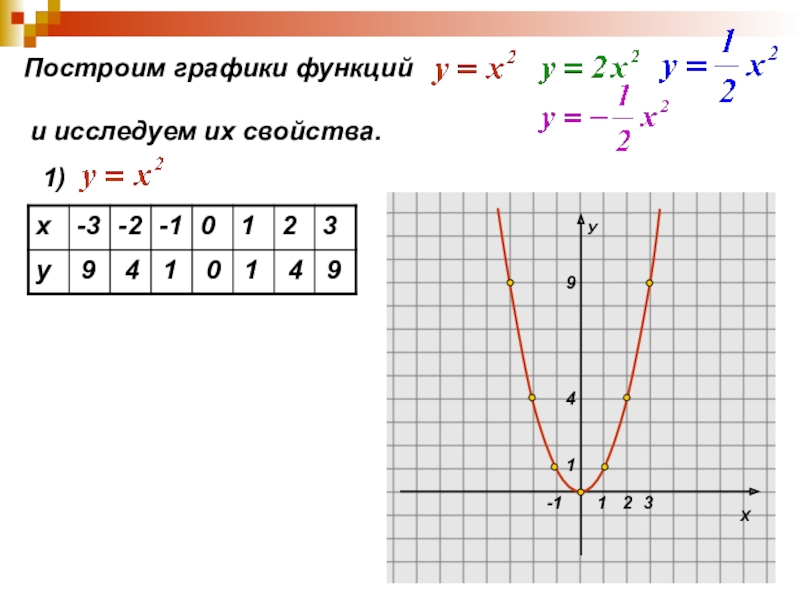
Слайд 7Построим графики функций
и исследуем их свойства.
1)
9
4
1
0
1
4
9
1. D(y):
2. у=0, если х=0
3. у>0, если х
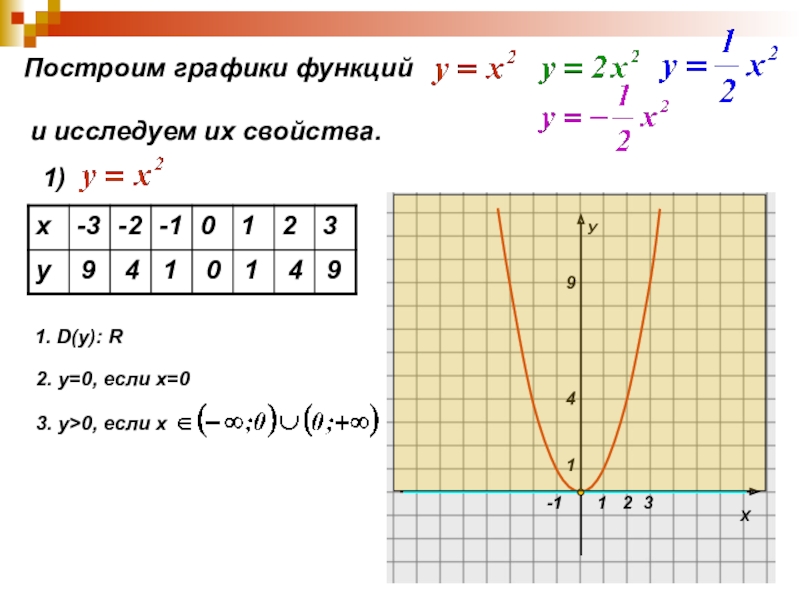
Слайд 8Построим графики функций
и исследуем их свойства.
1)
9
4
1
0
1
4
9
1. D(y):
2. у=0, если х=0
3. у>0, если х
4. у↓, если х
у↑, если х
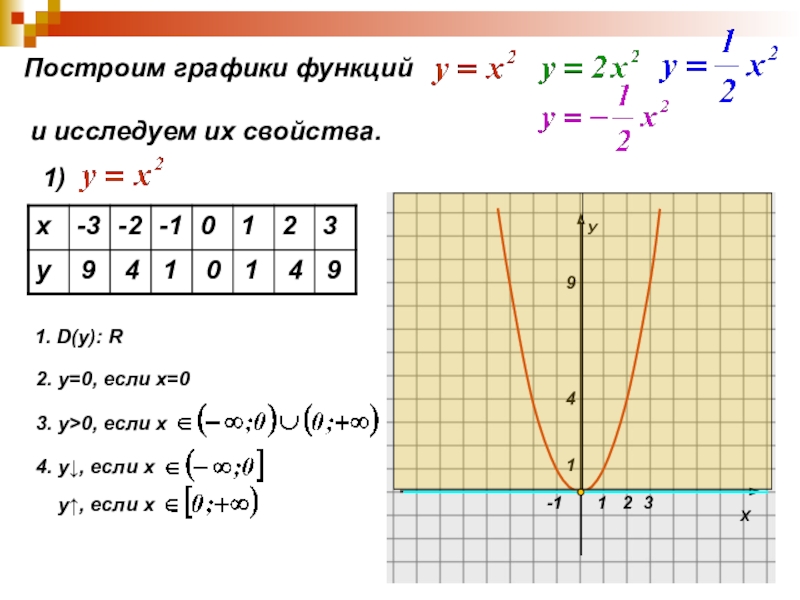
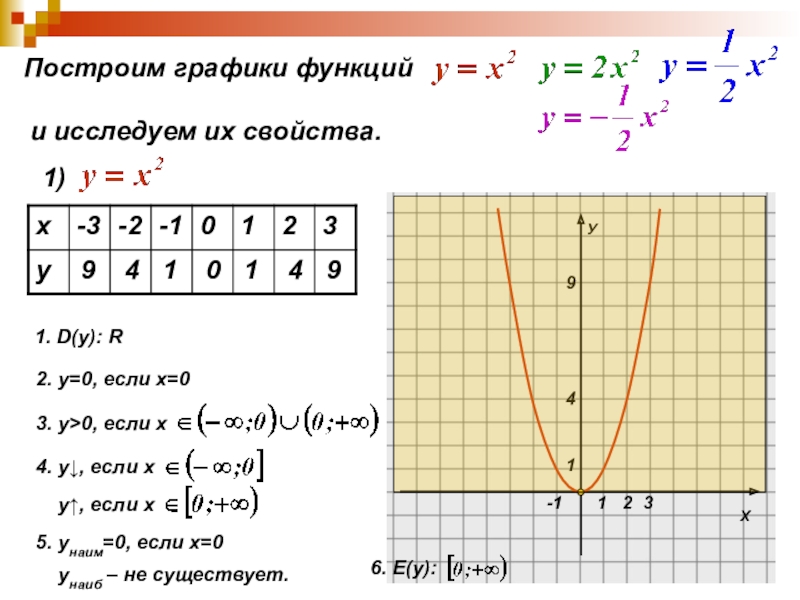
Слайд 9Построим графики функций
и исследуем их свойства.
1)
9
4
1
0
1
4
9
1. D(y):
2. у=0, если х=0
3. у>0, если х
4. у↓, если х
у↑, если х
5. унаим=0, если х=0
унаиб – не существует.
6. Е(y):
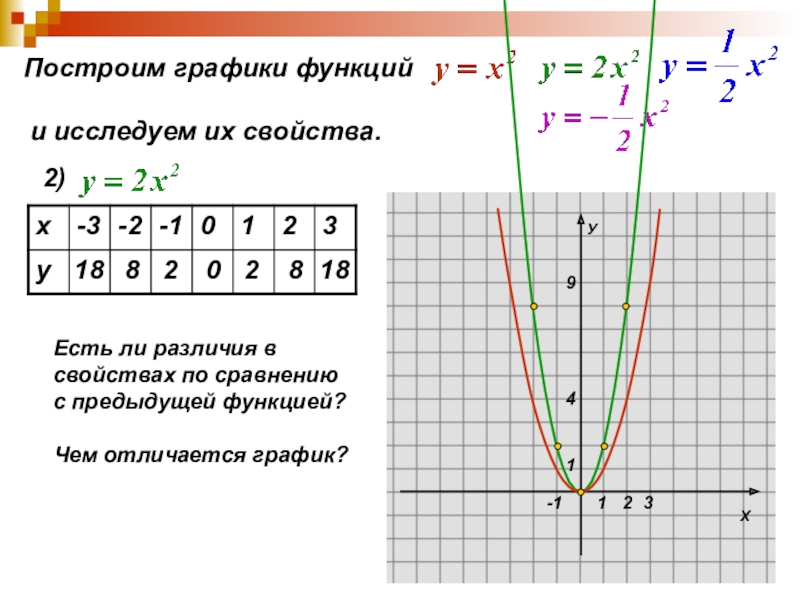
Слайд 10Построим графики функций
и исследуем их свойства.
2)
18
8
2
0
2
8
18
Есть ли
свойствах по сравнению
с предыдущей функцией?
Чем отличается график?
Слайд 11 График функции у=kx2 может быть получен из графика функции
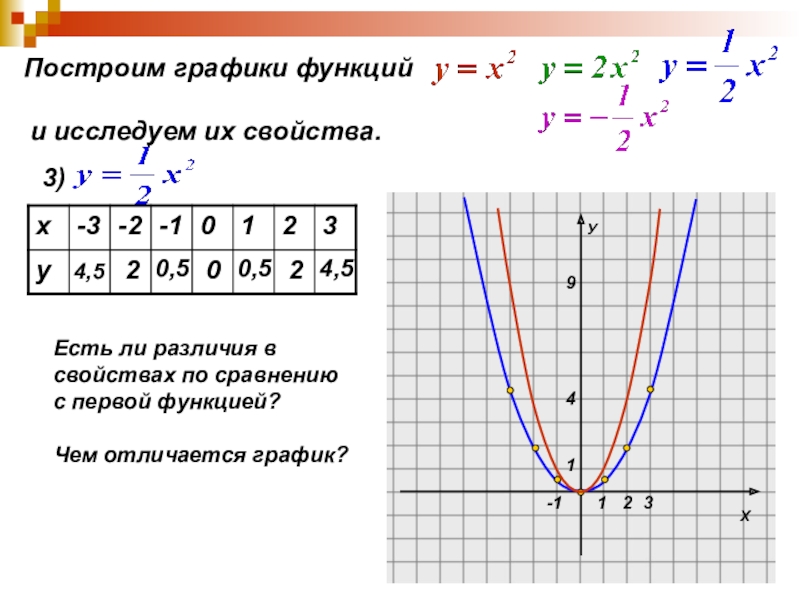
Слайд 12Построим графики функций
и исследуем их свойства.
3)
4,5
2
0,5
0
0,5
2
4,5
Есть ли
свойствах по сравнению
с первой функцией?
Чем отличается график?
Слайд 13 График функции у= x2 может
быть получен
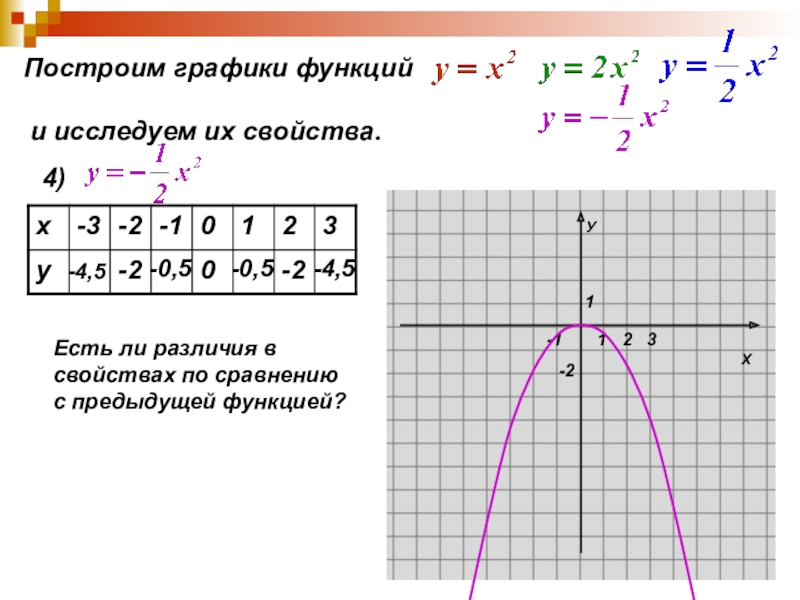
Слайд 14Построим графики функций
и исследуем их свойства.
4)
-4,5
-2
-0,5
0
-0,5
-2
-4,5
Есть ли
свойствах по сравнению
с предыдущей функцией?
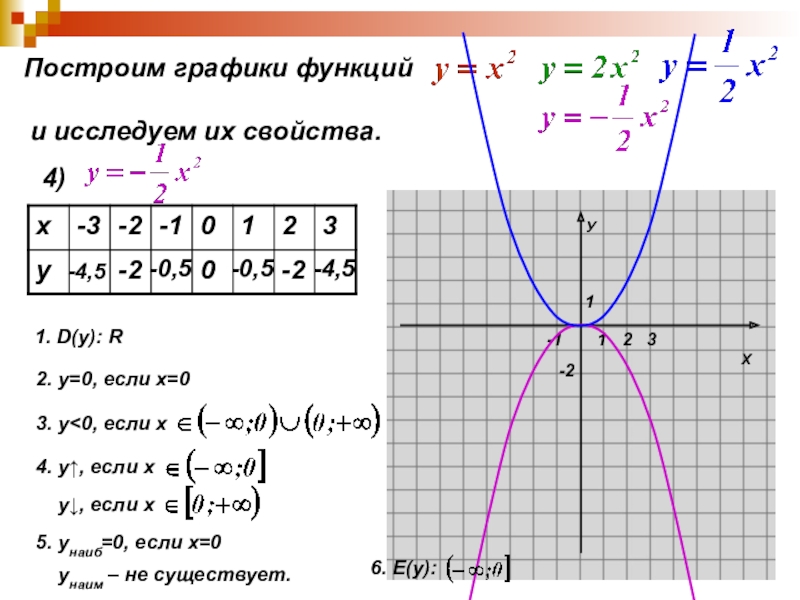
Слайд 15Построим графики функций
и исследуем их свойства.
4)
-4,5
-2
-0,5
0
-0,5
-2
-4,5
1. D(y):
2. у=0, если х=0
3. у<0, если х
4. у↑, если х
у↓, если х
5. унаиб=0, если х=0
унаим – не существует.
6. Е(y):
Слайд 16 График функции у=ах2 симметричен графику функции у=-ах2 относительно оси
Если а>0, то ветви параболы направлены…
Если а<0, то ветви параболы
направлены…